Skip to main content
欢迎来到PAWPAW技术文档网站，了解更多信息。

16-Bit complex BFP API

void bfp_complex_s16_init()​

初始化一个复数的16位BFP向量。

该函数初始化BFP向量a的各个字段。与复数的32位BFP向量（bfp_complex_s32_t）不同，为了进行各种优化，元素尾数的实部和虚部存储在单独的内存缓冲区中。

real_data指向用于存储实部的内存缓冲区。它的长度必须至少为length * 2字节，并且必须以字对齐的地址开始。

imag_data指向用于存储虚部的内存缓冲区。它的长度必须至少为length * 2字节，并且必须以字对齐的地址开始。

exp是分配给BFP向量的指数。初始化后，向量的第k个元素的逻辑值为 datak⋅2expdata_k \cdot 2^{exp}。

如果calc_hr为false，则a->hr初始化为0。否则，计算BFP向量的头空间并用于初始化a->hr。

参数:

  • bfp_complex_s16_t *a – [out] 要初始化的BFP向量

  • int16_t *real_data – [in] 用于存储a的实部的int16_t缓冲区

  • int16_t *imag_data – [in] 用于存储a的虚部的int16_t缓冲区

  • const exponent_t exp – [in] BFP向量的指数

  • const unsigned length– [in] BFP向量中的元素数量

  • const unsigned calc_hr – [in] 表示是否计算BFP向量的头空间的布尔值

参考性能:

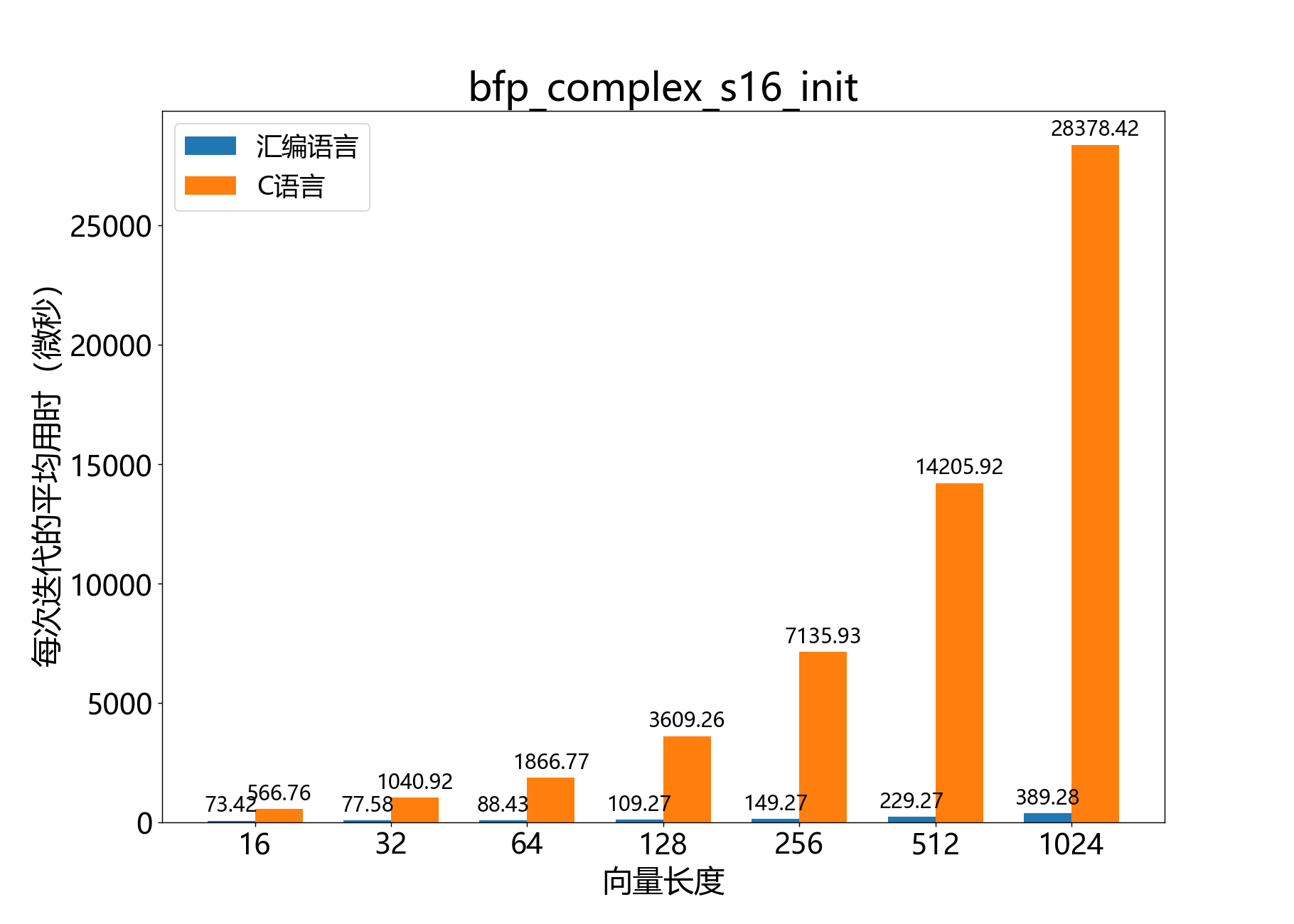
bfp_complex_s16_init

bfp_complex_s16_t bfp_complex_s16_alloc()​

从堆中动态分配一个复数的16位BFP向量。

如果分配失败，返回的向量的real和imag字段将为NULL，length字段将为零。否则，real和imag将指向分配的内存，length字段将是用户指定的长度。length参数不能为零。

该函数为实部和虚部分配了一个单独的内存块用于存储BFP向量。由于所有的BFP函数都要求尾数缓冲区从字对齐的地址开始，如果length是奇数，则该函数将为缓冲区分配额外的int16_t元素。

使用bfp_complex_s16_dealloc()释放使用该函数分配的BFP向量，以避免内存泄漏。

要使用静态内存分配初始化BFP向量，请使用bfp_complex_s16_init()。

参数:

  • const unsigned length– [in] 要分配的BFP向量的长度（以元素为单位）

返回值:

  • 复数的16位BFP向量

参考性能:

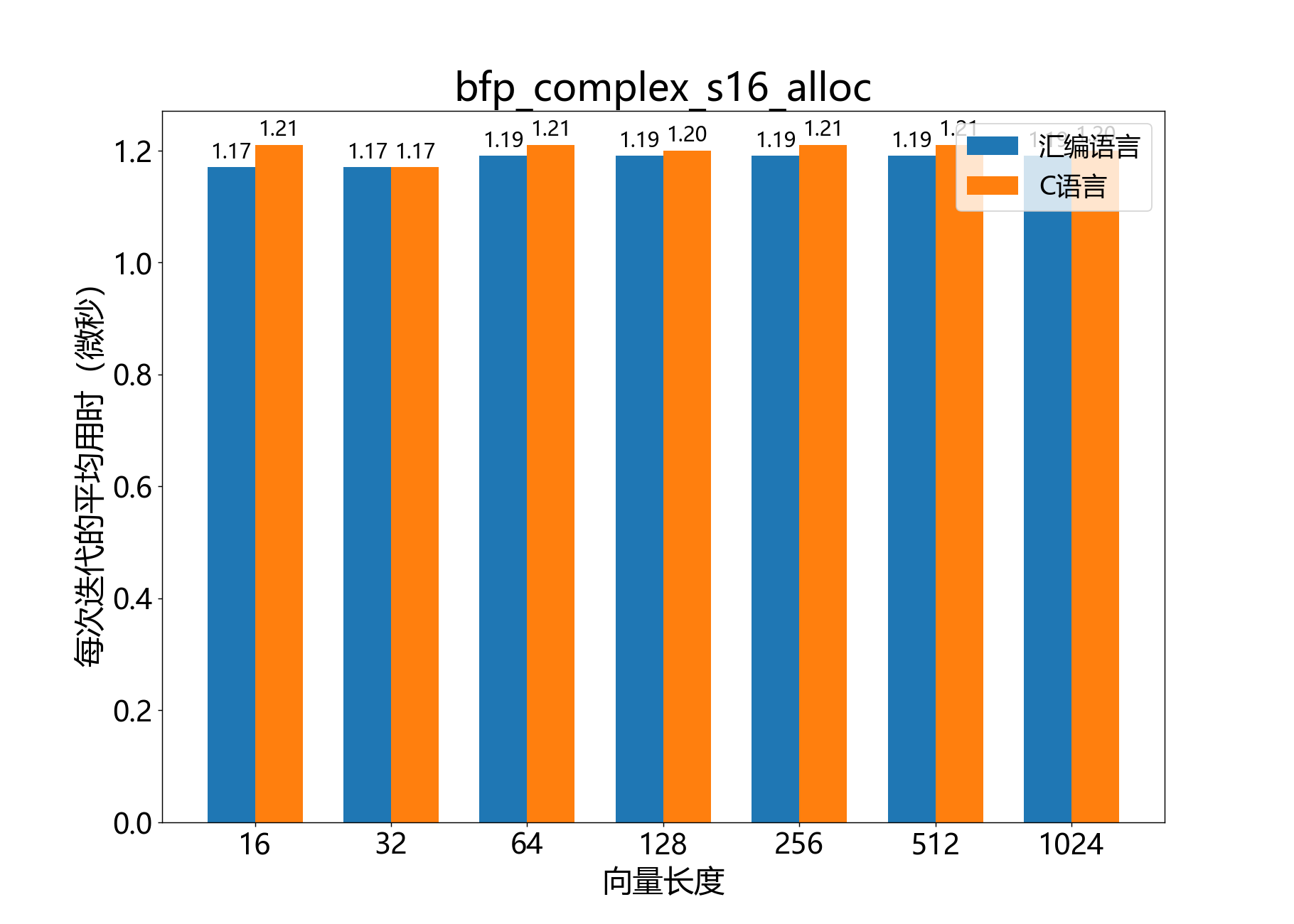
bfp_complex_s16_alloc

void bfp_complex_s16_dealloc()​

释放由bfp_complex_s16_alloc()分配的复数的16位BFP向量。

使用该函数释放bfp_complex_s16_alloc()分配的堆内存。

具有成功动态分配的尾数缓冲区的BFP向量有一个设置的标志。该函数可以安全地在任何未手动操作其flags或real的bfp_complex_s16_t上调用，包括：

  • 成功调用bfp_complex_s16_alloc()后得到的bfp_complex_s16_t
  • 不成功调用bfp_complex_s16_alloc()后得到的bfp_complex_s16_t
  • 使用bfp_complex_s16_init()初始化的bfp_complex_s16_t

对于后两种情况，该函数不执行任何操作。对于第一种情况，清除vector的real、imag、length和flags字段，使其为零。

参数:

  • bfp_complex_s16_t* vector – [in] 要释放的BFP向量。

参考性能:

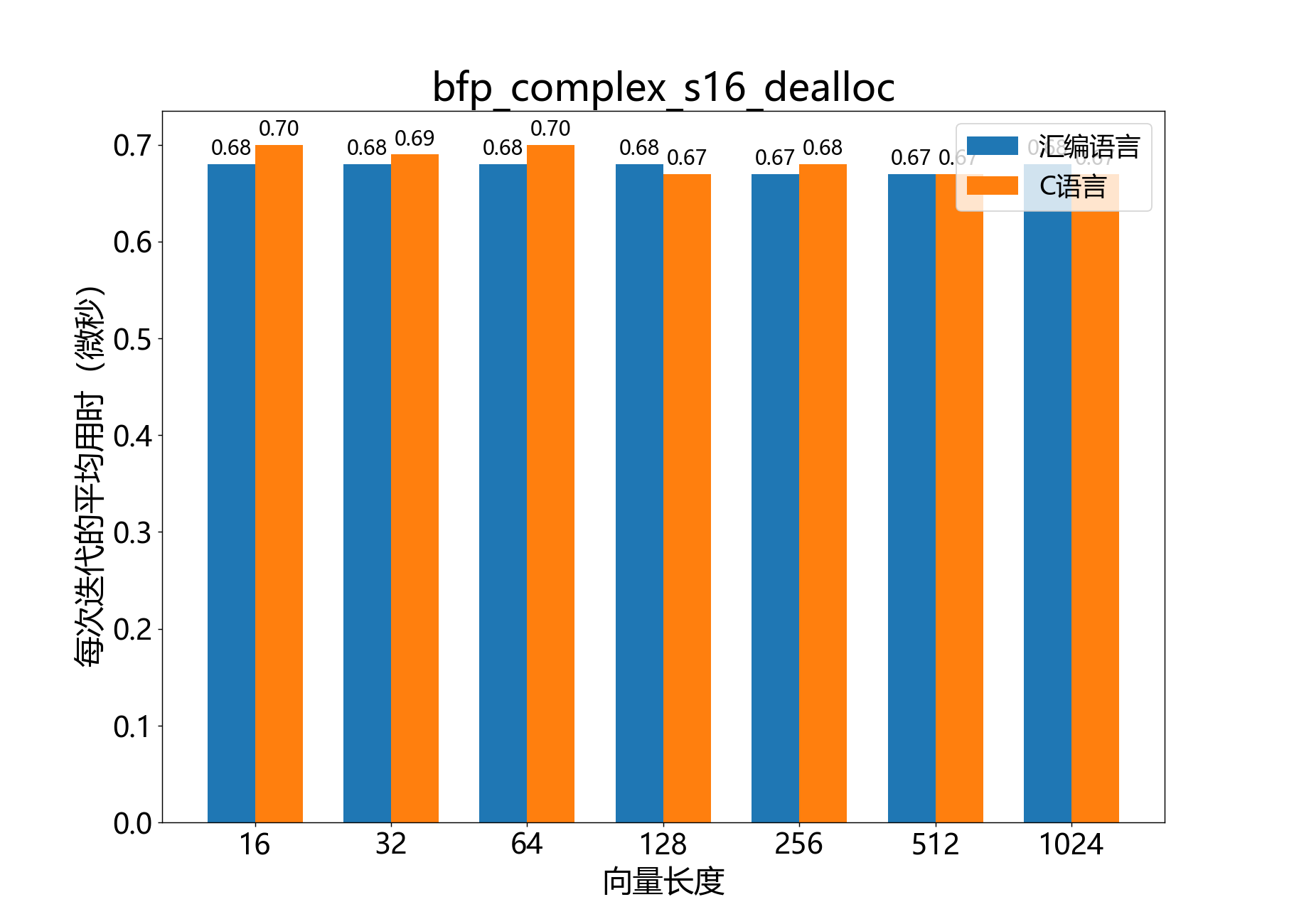
bfp_complex_s16_dealloc

void bfp_complex_s16_set()​

将复数的16位BFP向量的所有元素设置为指定值。

将a的指数设置为exp，并将每个元素的尾数设置为b。

执行此操作后，所有元素将表示相同的值 b⋅2expb \cdot 2^{exp}。

a必须已经被初始化（参见bfp_complex_s16_init()）。

参数:

  • bfp_complex_s16_t* a – [out] 要更新的BFP向量

  • const complex_s16_t b – [in] 每个复数尾数要设置的新值

  • const exponent_t exp – [in] BFP向量的新指数

参考性能:

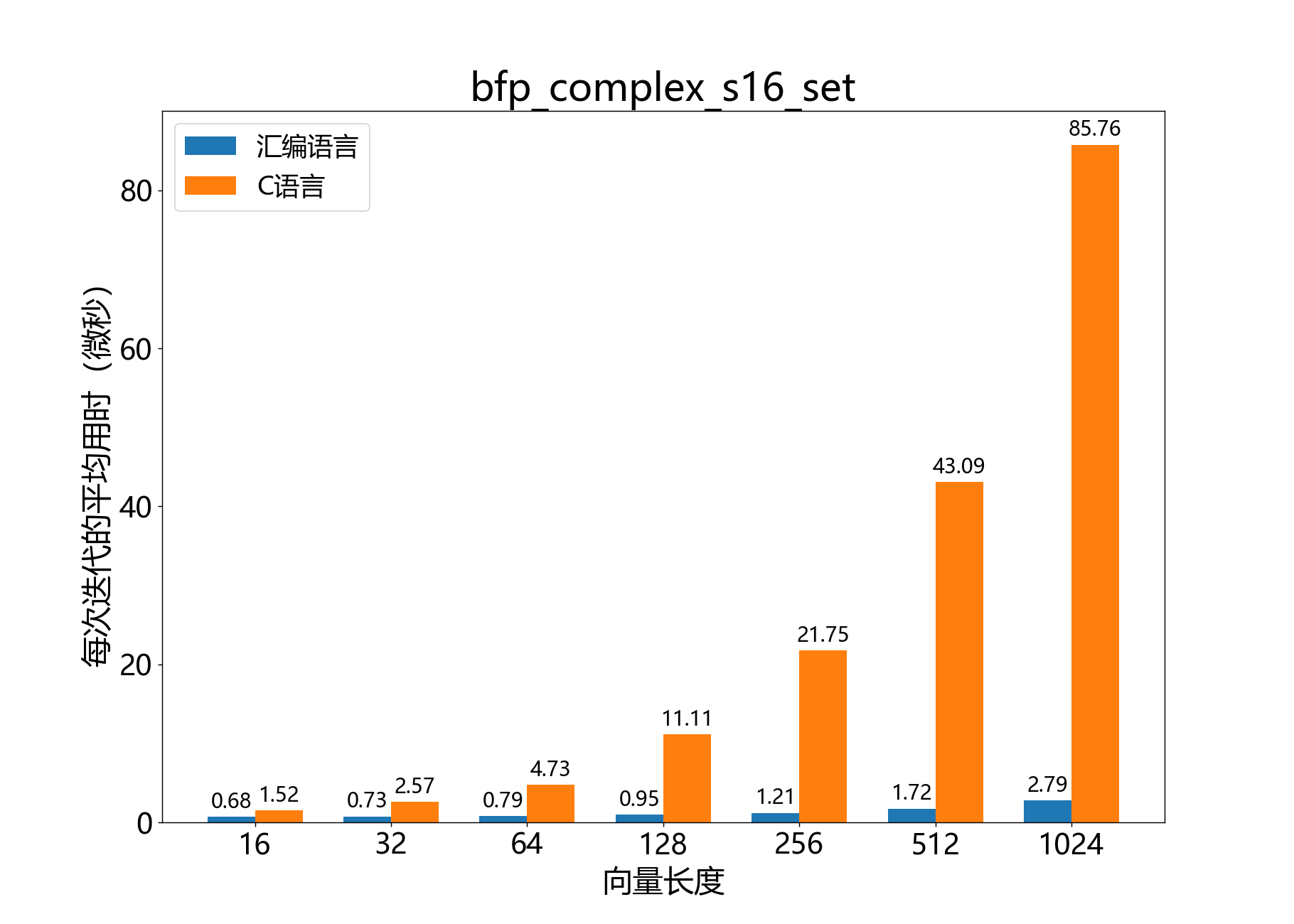
bfp_complex_s16_set

void bfp_complex_s16_use_exponent()​

将复数的16位BFP向量修改为使用指定的指数。

该函数强制复数BFP向量 Aˉ\bar A 使用指定的指数。尾数向量 aˉ\bar a 将被左移或右移以补偿改变的指数。

例如，在调用固定点算术函数之前，可以使用该函数确保底层尾数向量具有所需的Q格式。另一个例子是在与外围设备（例如通过I2S）通信时，可能需要将样本数据以指定格式呈现。

请注意，这设置了当前的编码，而不是永久地固定指数（即后续操作可能像往常一样更改指数）。

如果所需的固定点Q格式为QX.Y，其中Y是结果尾数中的小数位数，则关联的指数（和参数exp的值）为-Y。

a指向输入BFP向量 Aˉ\bar A，其中复数尾数向量为 aˉ\bar a，指数为 a_expa\_exp。a在原地更新，生成结果BFP向量 A~ˉ\bar{\tilde{A}}，其中复数尾数向量为 a~ˉ\bar{\tilde{a}}，指数为 a~_exp\tilde{a}\_exp。

exp为 a~_exp\tilde{a}\_exp，即所需的指数。Δp=a~_exp−a_exp\Delta{}p = \tilde{a}\_exp - a\_exp 是所需的指数变化量。

如果 Δp=0\Delta{}p = 0，则不修改BFP向量。

如果 Δp>0\Delta{}p > 0，则所需的指数大于当前指数，并且将对尾数 aˉ\bar a 进行 Δp\Delta{}p 位的算术右移。在进行右移时，通过丢弃 Δp\Delta{}p 个最低有效位可能会丢失精度。

如果 Δp<0\Delta{}p < 0，则所需的指数小于当前指数，并且将对尾数 aˉ\bar a 进行 Δp\Delta{}p 位的左移。在左移时，将应用饱和逻辑，以使任何无法使用新指数精确表示的元素饱和到16位饱和边界。

此函数会更新a的指数和头空间。

参数:

  • bfp_complex_s16_t* a – [in/out] 输入BFP向量 Aˉ\bar A / 输出BFP向量 A~ˉ\bar{\tilde{A}}
  • const exponent_t exp – [in] 所需的指数，a~_exp\tilde{a}\_exp

参考性能:

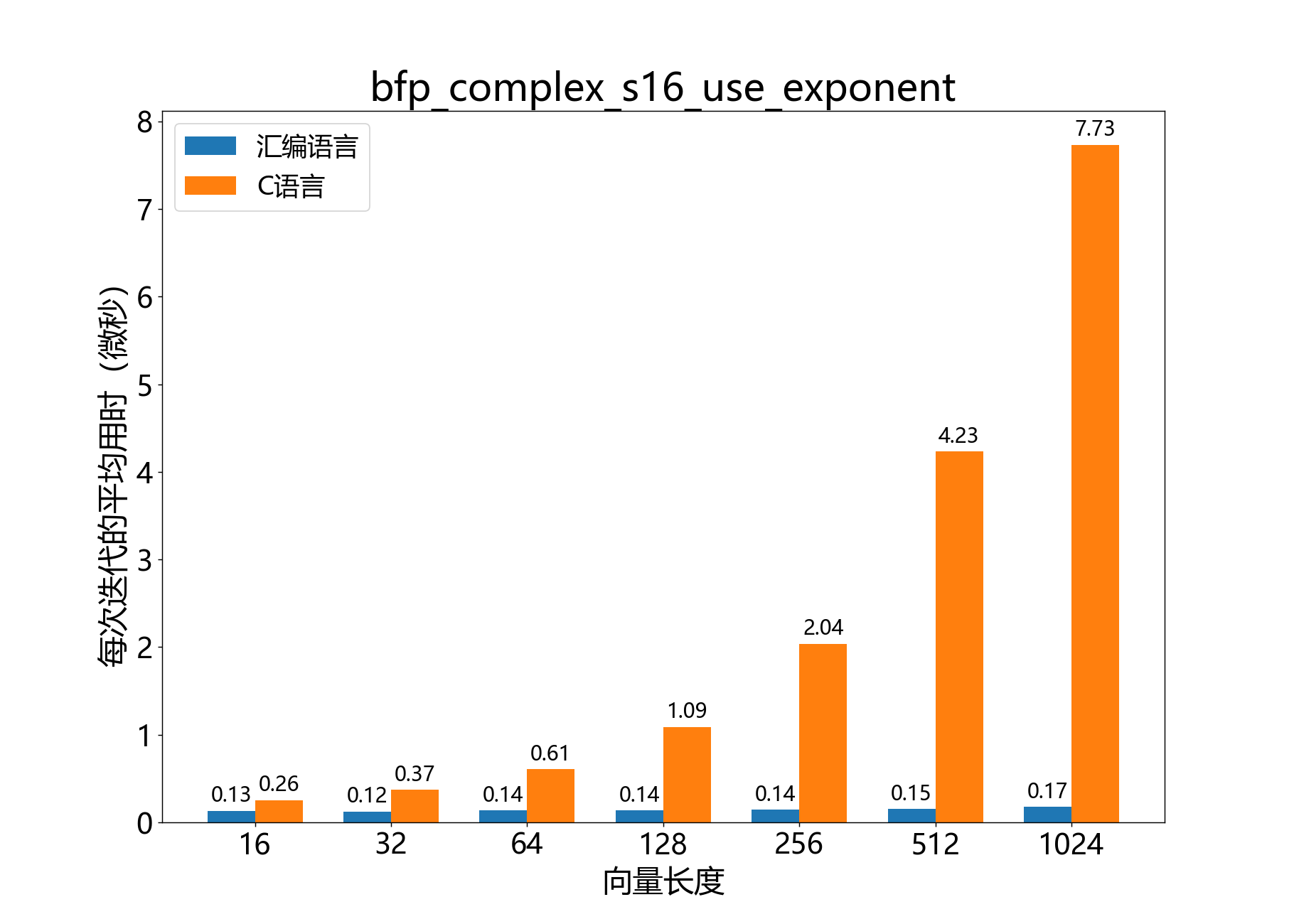
bfp_complex_s16_use_exponent

headroom_t bfp_complex_s16_headroom()​

获取复数16位BFP向量的头空间。

复数向量的头空间指的是每个元素的实部和虚部可以左移的位数，而不会丢失任何信息。它传达了向量可能包含的值的范围的信息，这对于确定如何在可能有损的块浮点运算中保持精度很有用。

在BFP的上下文中，头空间仅适用于尾数，不适用于指数。

特别地，如果复数16位尾数向量xˉ\bar{x}具有NN位的头空间，那么对于xˉ\bar{x}的任何元素xkx_k，有

−215−N≤Re{xk}<215−N-2^{15-N} \le Re\{x_k\} < 2^{15-N}

和

−215−N≤Im{xk}<215−N-2^{15-N} \le Im\{x_k\} < 2^{15-N}

对于复数BFP向量Xˉ\bar{X}的任何元素Xk=xk⋅2x_expX_k = x_k \cdot 2^{x\_exp}，有

−215+x_exp−N≤Re{Xk}<215+x_exp−N-2^{15 + x\_exp - N} \le Re\{X_k\} < 2^{15 + x\_exp - N}

和

−215+x_exp−N≤Im{Xk}<215+x_exp−N-2^{15 + x\_exp - N} \le Im\{X_k\} < 2^{15 + x\_exp - N}

该函数确定b的头空间，更新b->hr的值，并返回b->hr。

参数：

  • bfp_complex_s16_t *b – [in] 要获取头空间的复数BFP向量

返回值：

  • 复数BFP向量b的头空间

参考性能:

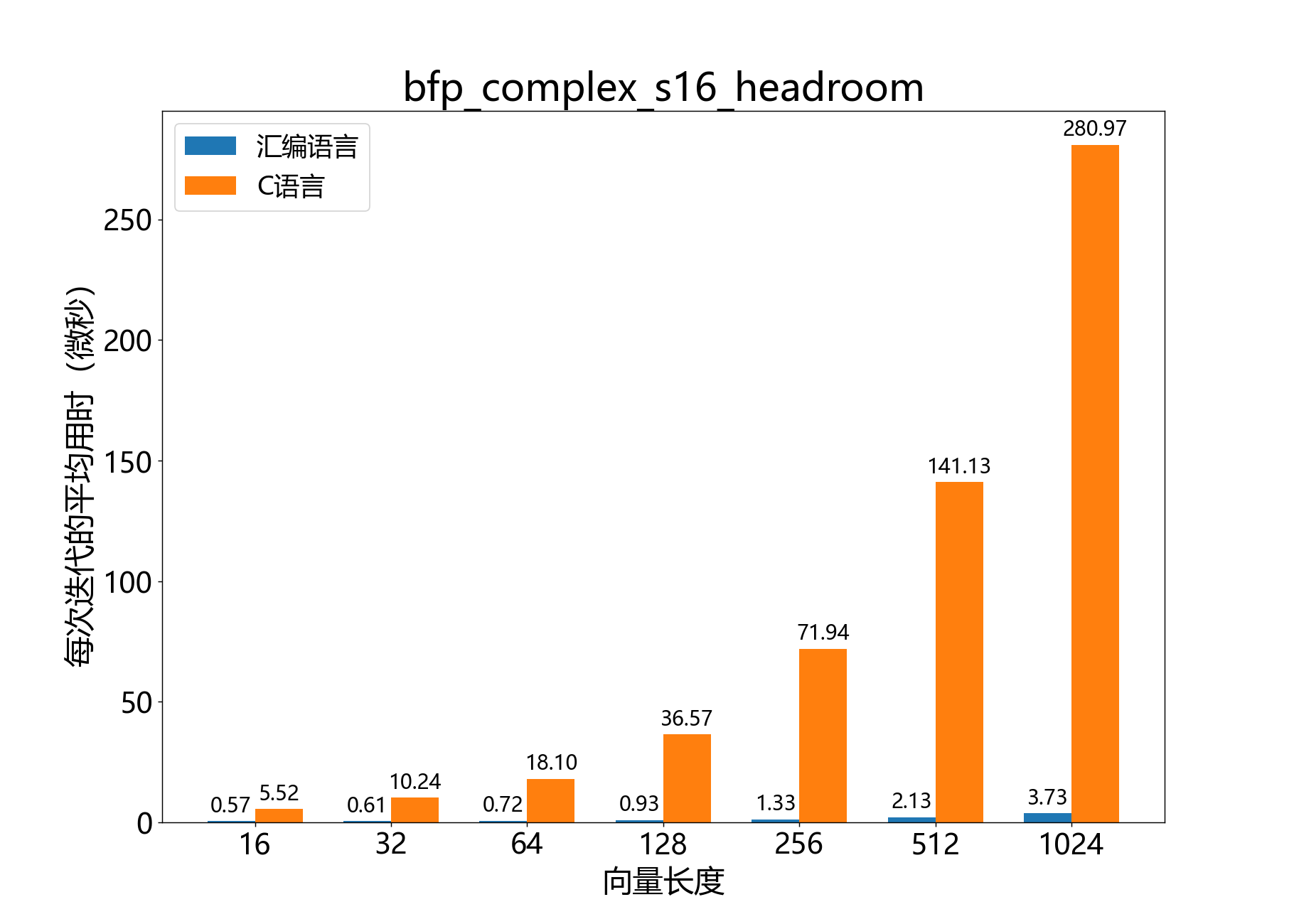
bfp_complex_s16_headroom

void bfp_complex_s16_shl()​

对复数16位BFP向量的尾数进行左移操作。

输入BFP向量Bˉ\bar{B}的每个复数尾数将左移b_shl位，并存储在输出BFP向量Aˉ\bar{A}的相应元素中。

此操作可用于为BFP向量添加或删除头空间。

b_shl是每个尾数的实部和虚部将左移的位数。这个左移是有符号的算术左移，因此b_shl为负值时，尾数将右移。

a和b必须已经初始化（参见bfp_complex_s16_init()），并且长度必须相同。

此操作可以安全地在b上原地执行。

请注意，此操作绕过了保护调用者免受饱和或下溢的逻辑。输出值饱和到对称的16位范围（开区间(−215,215)(-2^{15}, 2^{15})）。为避免饱和，b_shl应不大于b的头空间（b->hr）。

操作：

Re{ak}←sat16(⌊Re{bk}⋅2b_shl⌋)Im{ak}←sat16(⌊Im{bk}⋅2b_shl⌋)对于 k∈0 ... (N−1)其中 N 是 Bˉ 的长度而 bk 和 ak 分别表示 Bˉ 和 Aˉ 中的第 k 个尾数\begin{split}\begin{align*} & Re\{a_k\} \leftarrow sat_{16}( \lfloor Re\{b_k\} \cdot 2^{b\_shl} \rfloor ) \\ & Im\{a_k\} \leftarrow sat_{16}( \lfloor Im\{b_k\} \cdot 2^{b\_shl} \rfloor ) \\ & \qquad\text{对于 } k \in 0\ ...\ (N-1) \\ & \qquad\text{其中 } N \text{ 是 } \bar{B} \text{ 的长度} \\ & \qquad\text{而 } b_k \text{ 和 } a_k \text{ 分别表示 } \bar{B} \text{ 和 } \bar{A} \text{ 中的第 } k \text{ 个尾数} && \end{align*}\end{split}

参数：

  • bfp_complex_s16_t *a – [out] 复数输出BFP向量Aˉ\bar{A}
  • const bfp_complex_s16_t *b – [in] 复数输入BFP向量Bˉ\bar{B}
  • const left_shift_t b_shl – [in] 应用于Bˉ\bar{B}的尾数的有符号算术左移位数。

参考性能:

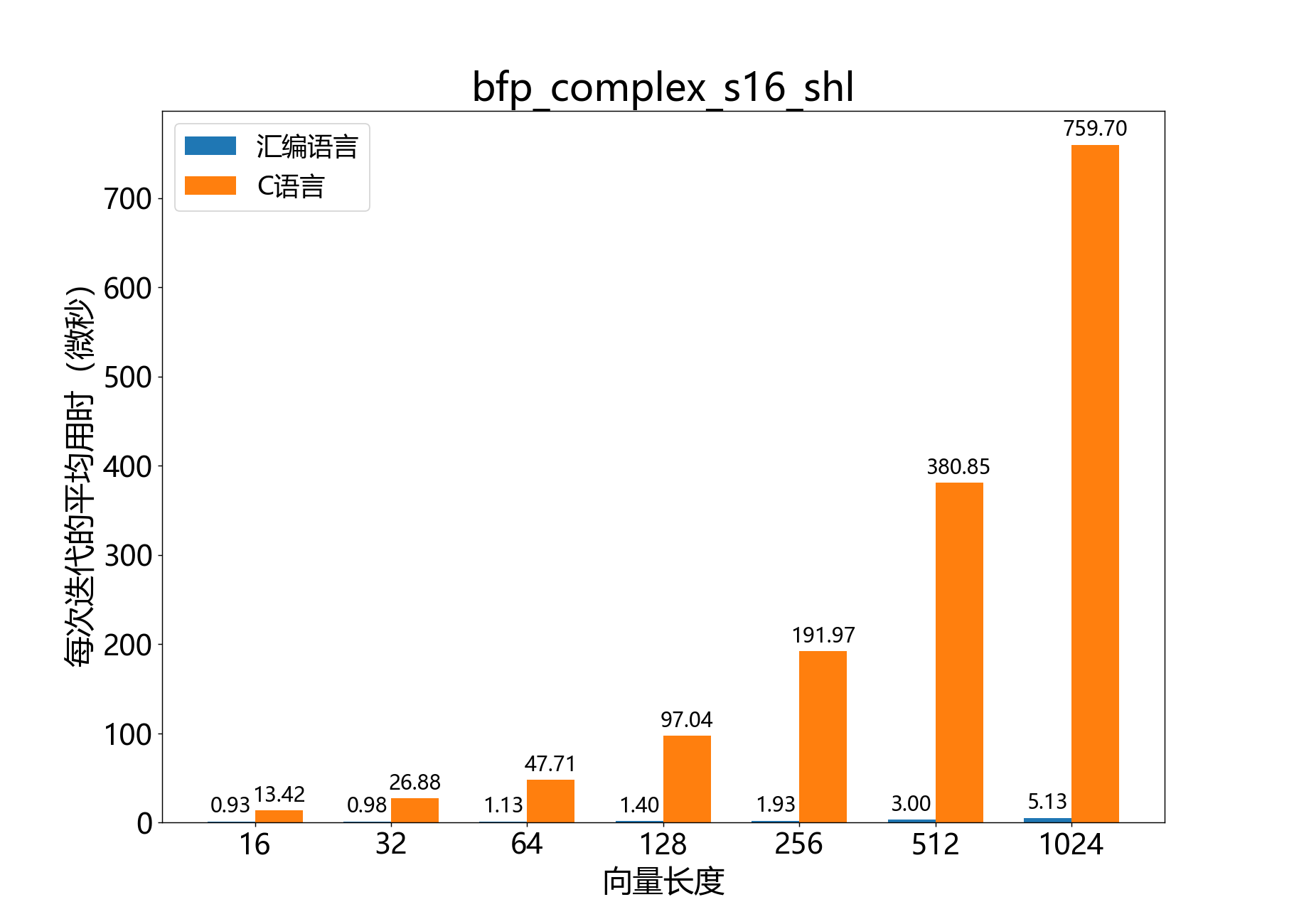
bfp_complex_s16_shl

void bfp_complex_s16_real_mul()​

将复数16位BFP向量逐元素与实数16位BFP向量相乘。

复数输出BFP向量Aˉ\bar{A}的每个复数输出元素AkA_k被设置为复数输入BFP向量Bˉ\bar{B}和实数输入BFP向量Cˉ\bar{C}的相应元素BkB_k和CkC_k的复数乘积。

a，b和c必须已经初始化（参见bfp_complex_s16_init()和bfp_s16_init()），并且长度必须相同。

此操作可以安全地在b上原地执行。

操作：

Ak←Bk⋅Ck对于 k∈0 ... (N−1)其中 N 是 Bˉ 和 Cˉ 的长度\begin{align*} A_k &\leftarrow B_k \cdot C_k \\ &\text{对于 } k \in 0\ ...\ (N-1) \\ &\text{其中 } N \text{ 是 } \bar{B} \text{ 和 } \bar{C} \text{ 的长度} \end{align*}

参数：

  • bfp_complex_s16_t *a – [out] 输出复数BFP向量Aˉ\bar{A}
  • const bfp_complex_s16_t *b – [in] 输入复数BFP向量Bˉ\bar{B}
  • const bfp_s16_t *c – [in] 输入实数BFP向量Cˉ\bar{C}

参考性能:

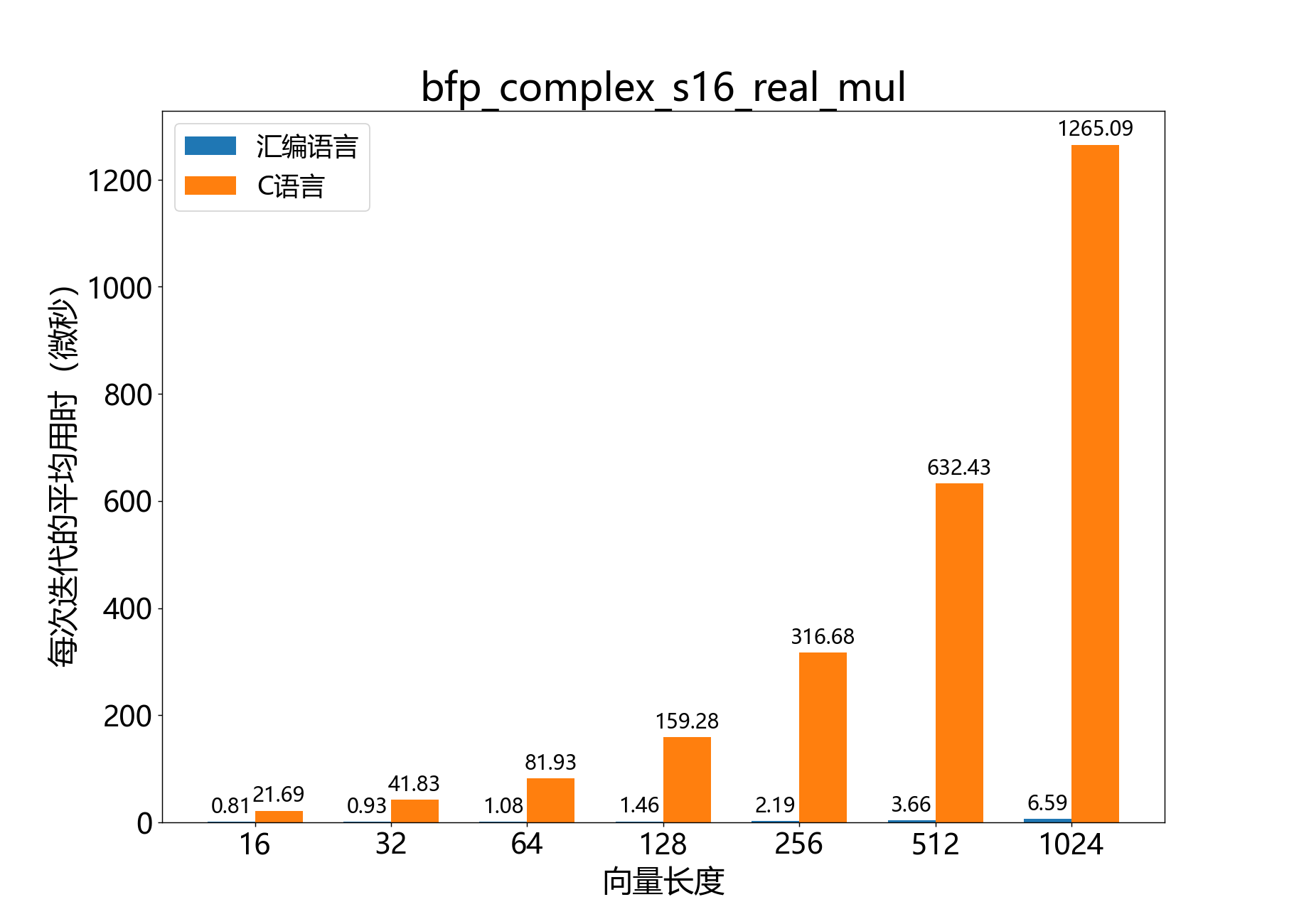
bfp_complex_s16_real_mul

void bfp_complex_s16_mul()​

将一个复数16位BFP向量逐元素与另一个复数16位BFP向量相乘。

复数输出BFP向量Aˉ\bar{A}的每个复数输出元素AkA_k被设置为复数输入BFP向量Bˉ\bar{B}和Cˉ\bar{C}的相应元素BkB_k和CkC_k的复数乘积。

a，b和c必须已经初始化（参见bfp_complex_s16_init()），并且长度必须相同。

此操作可以安全地在b或c上原地执行。

操作：

Ak←Bk⋅Ck对于 k∈0 ... (N−1)其中 N 是 Bˉ 和 Cˉ 的长度\begin{align*} A_k &\leftarrow B_k \cdot C_k \\ &\text{对于 } k \in 0\ ...\ (N-1) \\ &\text{其中 } N \text{ 是 } \bar{B} \text{ 和 } \bar{C} \text{ 的长度} \end{align*}

参数：

  • bfp_complex_s16_t *a – [out] 输出复数BFP向量Aˉ\bar{A}
  • const bfp_complex_s16_t *b – [in] 输入复数BFP向量Bˉ\bar{B}
  • const bfp_complex_s16_t *c – [in] 输入复数BFP向量Cˉ\bar{C}

参考性能:

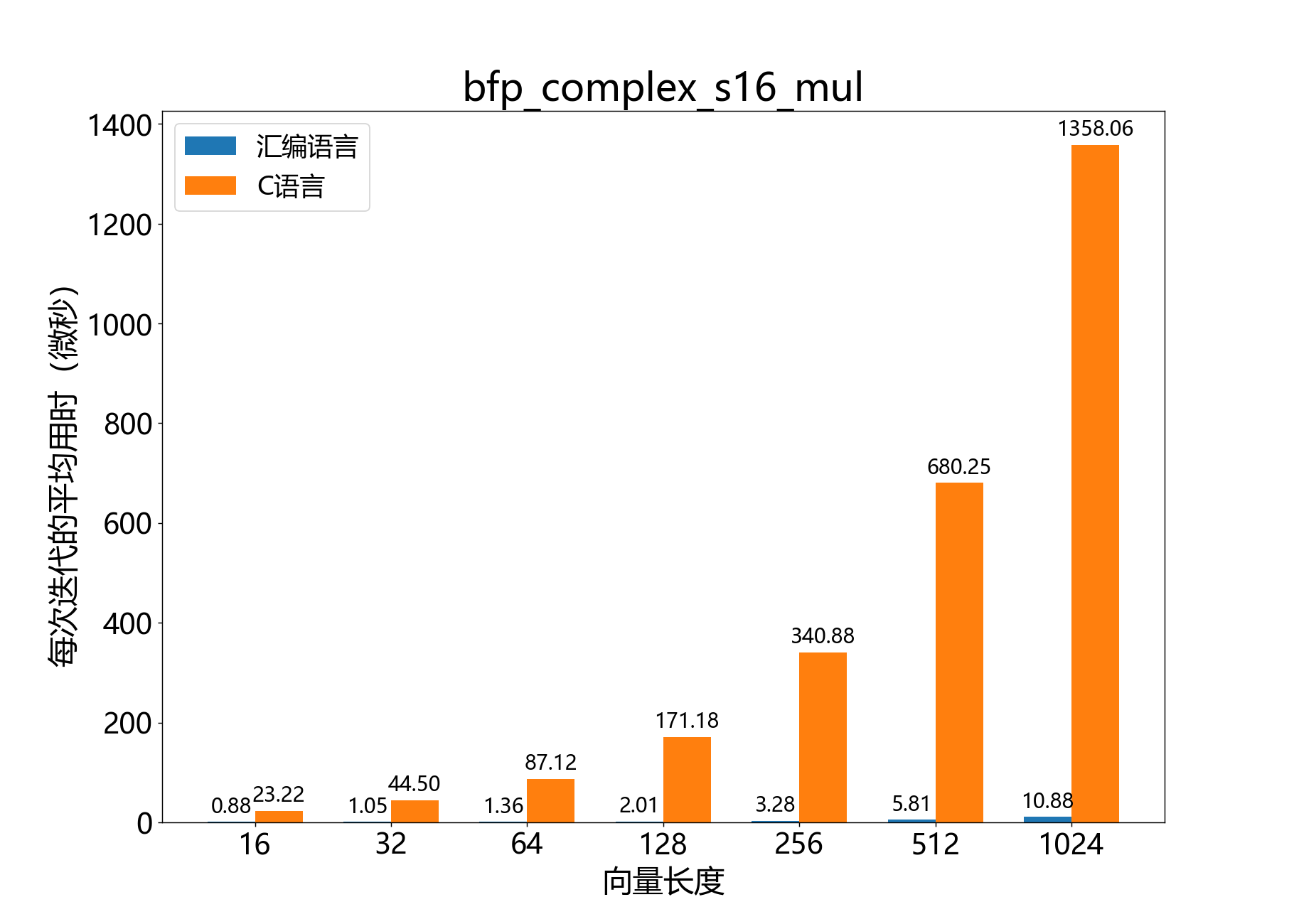
bfp_complex_s16_mul

void bfp_complex_s16_conj_mul()​

将一个复数16位BFP向量逐元素与另一个的复数共轭相乘。

复数输出BFP向量Aˉ\bar{A}的每个复数输出元素AkA_k被设置为复数输入BFP向量Bˉ\bar{B}的相应元素BkB_k与复数输入BFP向量Cˉ\bar{C}的相应元素(Ck)∗(C_k)^*的复数乘积。

操作：

Ak←Bk⋅(Ck)∗对于 k∈0 ... (N−1)其中 N 是 Bˉ 和 Cˉ 的长度(Ck)∗是 Ck 的复数共轭\begin{align*} A_k &\leftarrow B_k \cdot (C_k)^* \\ &\text{对于 } k \in 0\ ...\ (N-1) \\ &\text{其中 } N \text{ 是 } \bar{B} \text{ 和 } \bar{C} \text{ 的长度} \\ &(C_k)^* \text{是 } C_k \text{ 的复数共轭} \end{align*}

参数：

  • bfp_complex_s16_t *a – [out] 输出复数BFP向量Aˉ\bar{A}
  • const bfp_complex_s16_t *b – [in] 输入复数BFP向量Bˉ\bar{B}
  • const bfp_complex_s16_t *c – [in] 输入复数BFP向量Cˉ\bar{C}

参考性能:

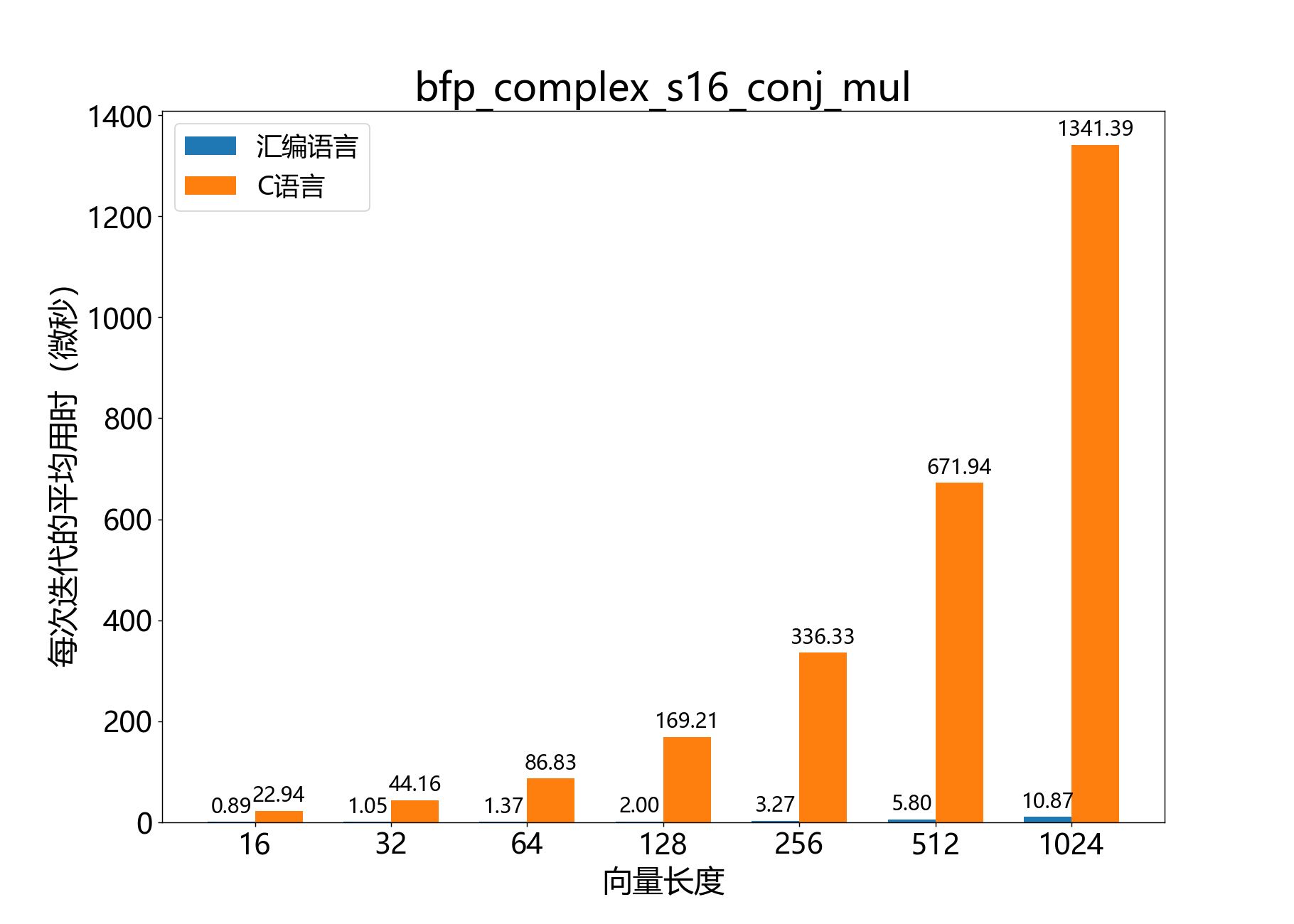
bfp_complex_s16_conj_mul

void bfp_complex_s16_macc()​

将一个复数16位BFP向量逐元素与另一个复数16位BFP向量相乘，并将结果加到第三个向量上。

操作：

Ak←Ak+(Bk⋅Ck)对于 k∈0 ... (N−1)其中 N 是 Bˉ 和 Cˉ 的长度\begin{align*} A_k &\leftarrow A_k + (B_k \cdot C_k) \\ &\text{对于 } k \in 0\ ...\ (N-1) \\ &\text{其中 } N \text{ 是 } \bar{B} \text{ 和 } \bar{C} \text{ 的长度} \end{align*}

参数：

  • bfp_complex_s16_t *acc – [in/out] 输入/输出累加器复数BFP向量Aˉ\bar{A}
  • const bfp_complex_s16_t *b – [in] 输入复数BFP向量Bˉ\bar{B}
  • const bfp_complex_s16_t *c – [in] 输入复数BFP向量Cˉ\bar{C}

参考性能:

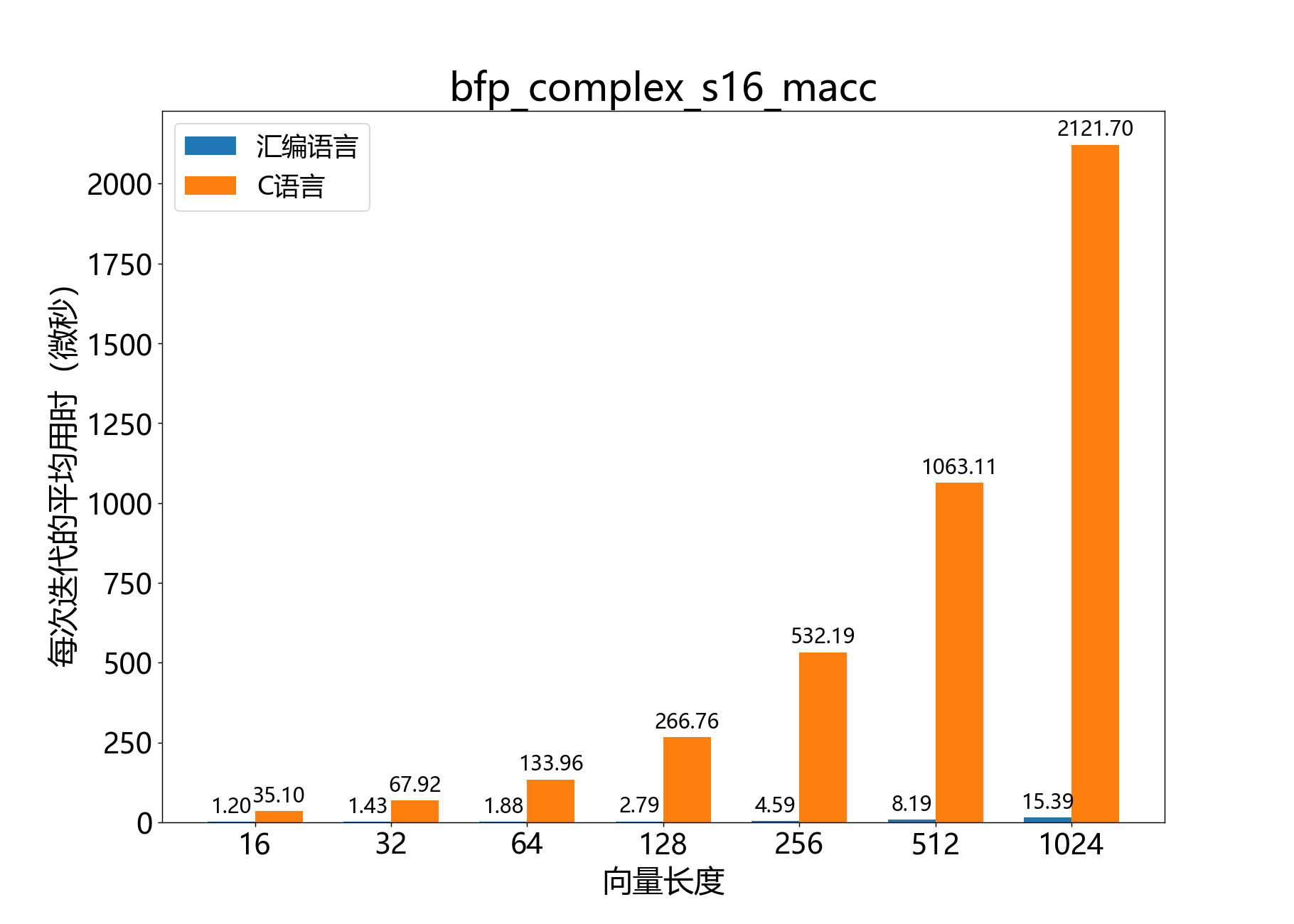
bfp_complex_s16_macc

void bfp_complex_s16_nmacc()​

逐元素将一个复数16位BFP向量与另一个向量相乘，并从第三个向量中减去结果。

操作：

Ak←Ak−(Bk⋅Ck)其中k∈0 ... (N−1),其中N是向量Bˉ和Cˉ的长度。\begin{align*} A_k &\leftarrow A_k - (B_k \cdot C_k) \\ &\text{其中} k \in 0\ ...\ (N-1), \\ &\text{其中} N \text{是向量} \bar{B} \text{和} \bar{C} \text{的长度。} \end{align*}

参数：

  • bfp_complex_s16_t* acc – [inout] 输入/输出累加器复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const bfp_complex_s16_t* c – [in] 输入复数BFP向量 Cˉ\bar{C}

参考性能:

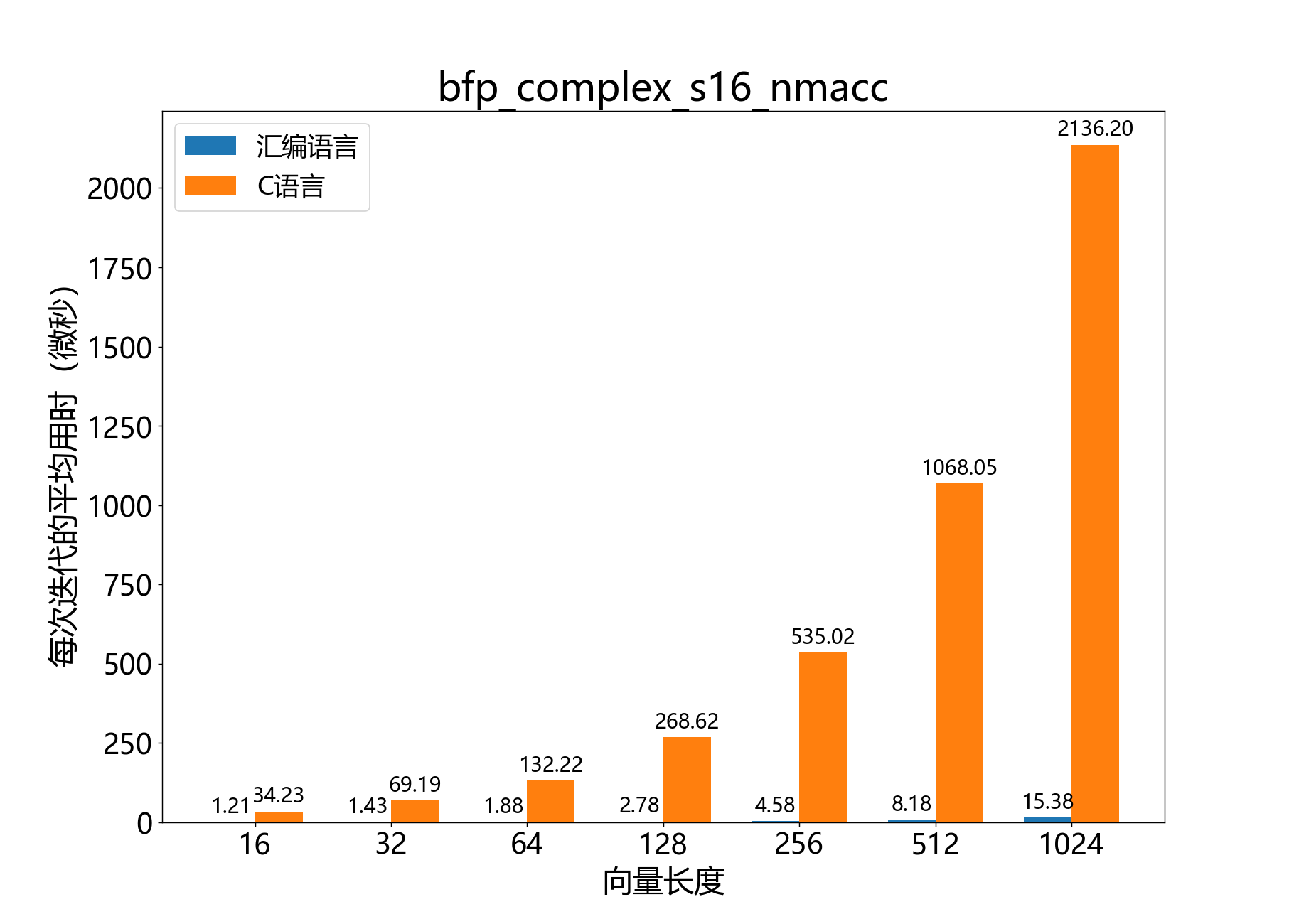
bfp_complex_s16_nmacc

void bfp_complex_s16_conj_macc()​

逐元素将一个复数16位BFP向量与另一个向量的复共轭相乘，并将结果加到第三个向量中。

操作：

Ak←Ak+(Bk⋅Ck∗)其中k∈0 ... (N−1),其中N是向量Bˉ和Cˉ的长度。(Ck)∗表示Ck的复共轭。\begin{align*} A_k &\leftarrow A_k + (B_k \cdot C_k^*) \\ &\text{其中} k \in 0\ ...\ (N-1), \\ &\text{其中} N \text{是向量} \bar{B} \text{和} \bar{C} \text{的长度。} \\ &(C_k)^* \text{表示} C_k \text{的复共轭。} \end{align*}

参数：

  • bfp_complex_s16_t* acc – [inout] 输入/输出累加器复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const bfp_complex_s16_t* c – [in] 输入复数BFP向量 Cˉ\bar{C}

参考性能:

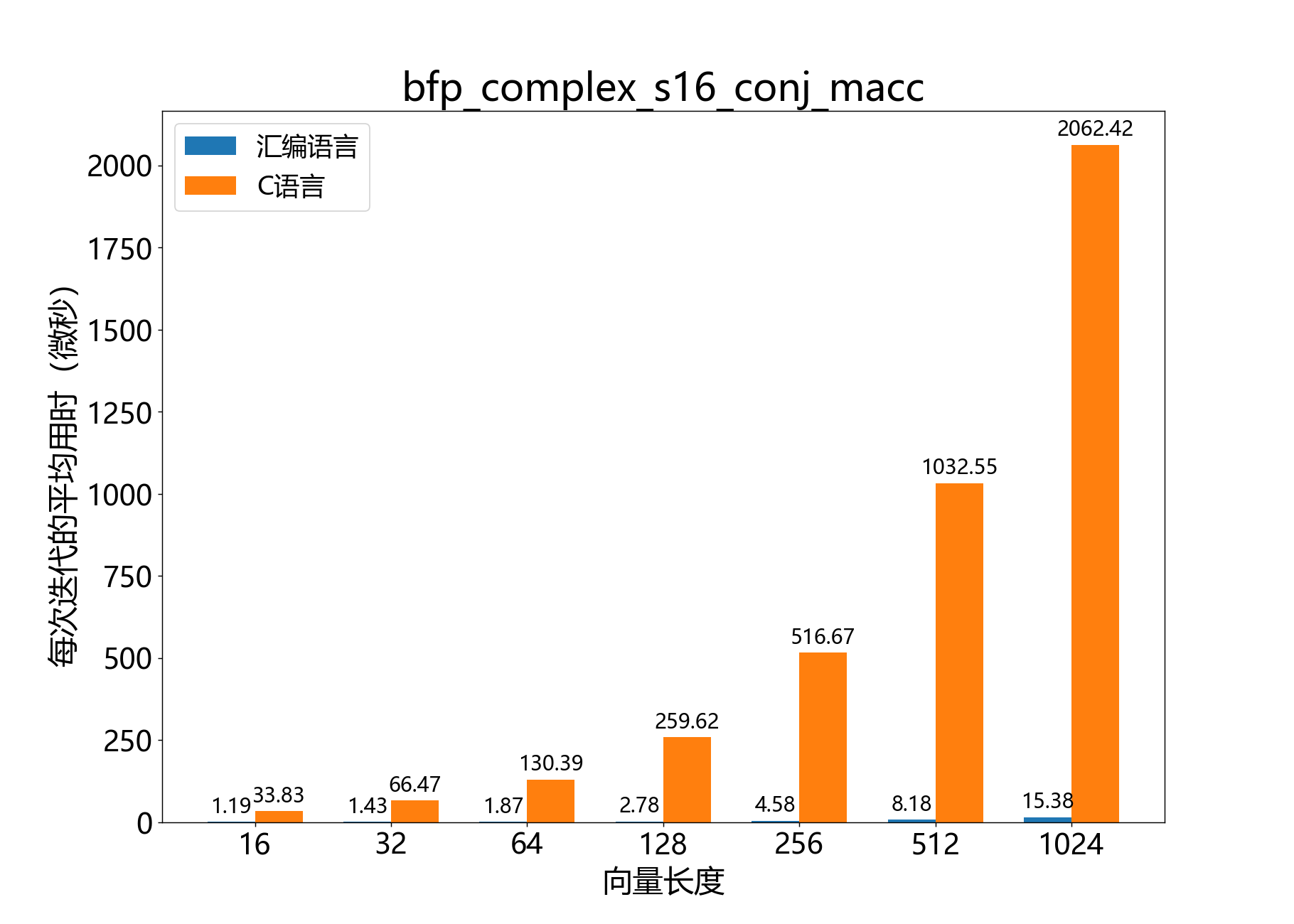
bfp_complex_s16_conj_macc

void bfp_complex_s16_conj_nmacc()​

逐元素将一个复数16位BFP向量与另一个向量的复共轭相乘，并从第三个向量中减去结果。

操作：

Ak←Ak−(Bk⋅Ck∗)其中k∈0 ... (N−1),其中N是向量Bˉ和Cˉ的长度。(Ck)∗表示Ck的复共轭。\begin{align*} A_k &\leftarrow A_k - (B_k \cdot C_k^*) \\ &\text{其中} k \in 0\ ...\ (N-1), \\ &\text{其中} N \text{是向量} \bar{B} \text{和} \bar{C} \text{的长度。} \\ &(C_k)^* \text{表示} C_k \text{的复共轭。} \end{align*}

参数：

  • bfp_complex_s16_t* acc – [inout] 输入/输出累加器复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const bfp_complex_s16_t* c – [in] 输入复数BFP向量 Cˉ\bar{C}

参考性能:

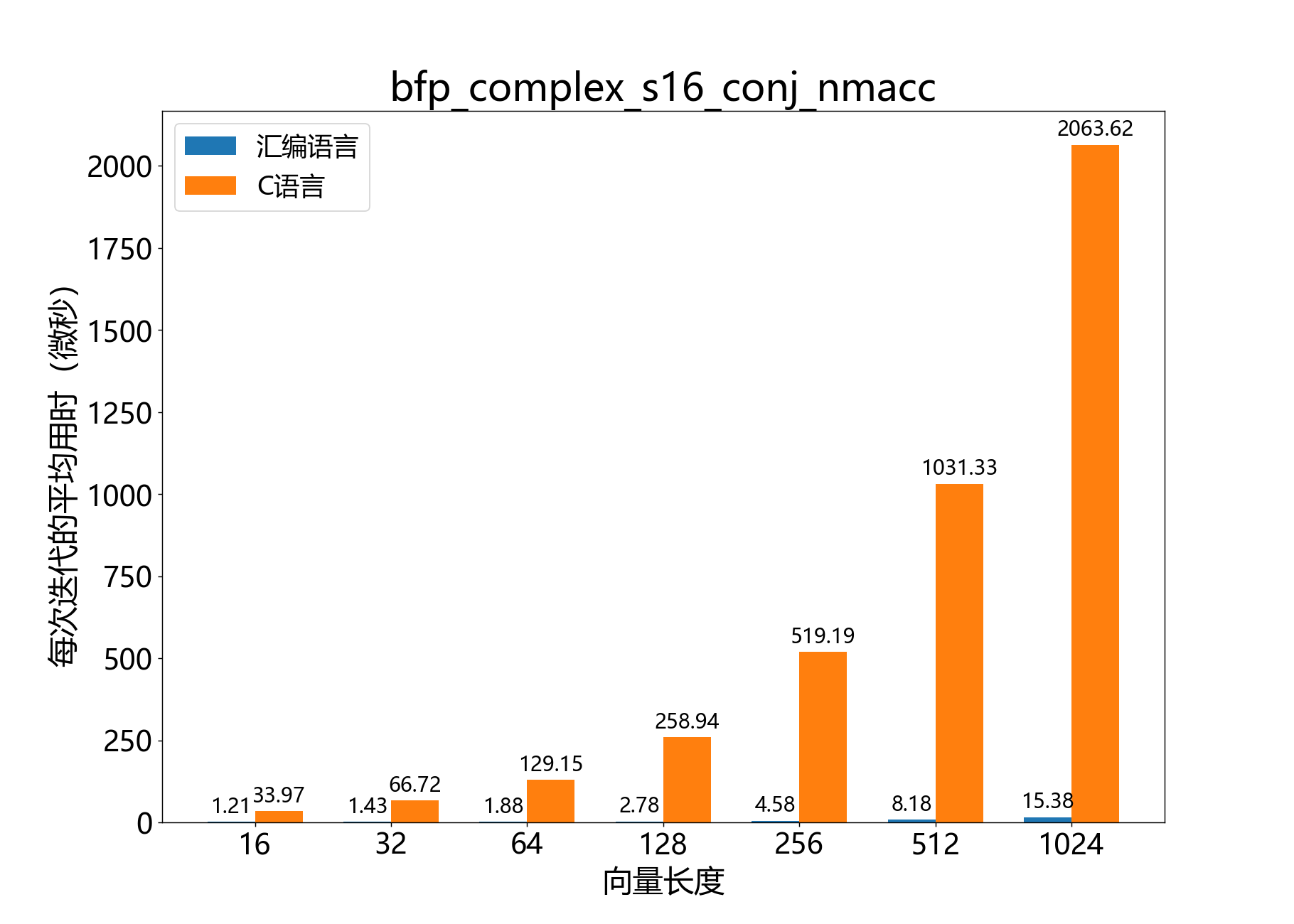
bfp_complex_s16_conj_nmacc

void bfp_complex_s16_real_scale()​

将一个复数16位BFP向量乘以一个实数标量。

操作：

Aˉ←Bˉ⋅(α⋅2α_exp)\bar{A} \leftarrow \bar{B} \cdot \left( \alpha \cdot 2^{\alpha\_exp} \right)

参数：

  • bfp_complex_s16_t* a – [out] 输出复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const float alpha – [in] 乘以 Bˉ\bar{B} 的实数标量 α\alpha

参考性能:

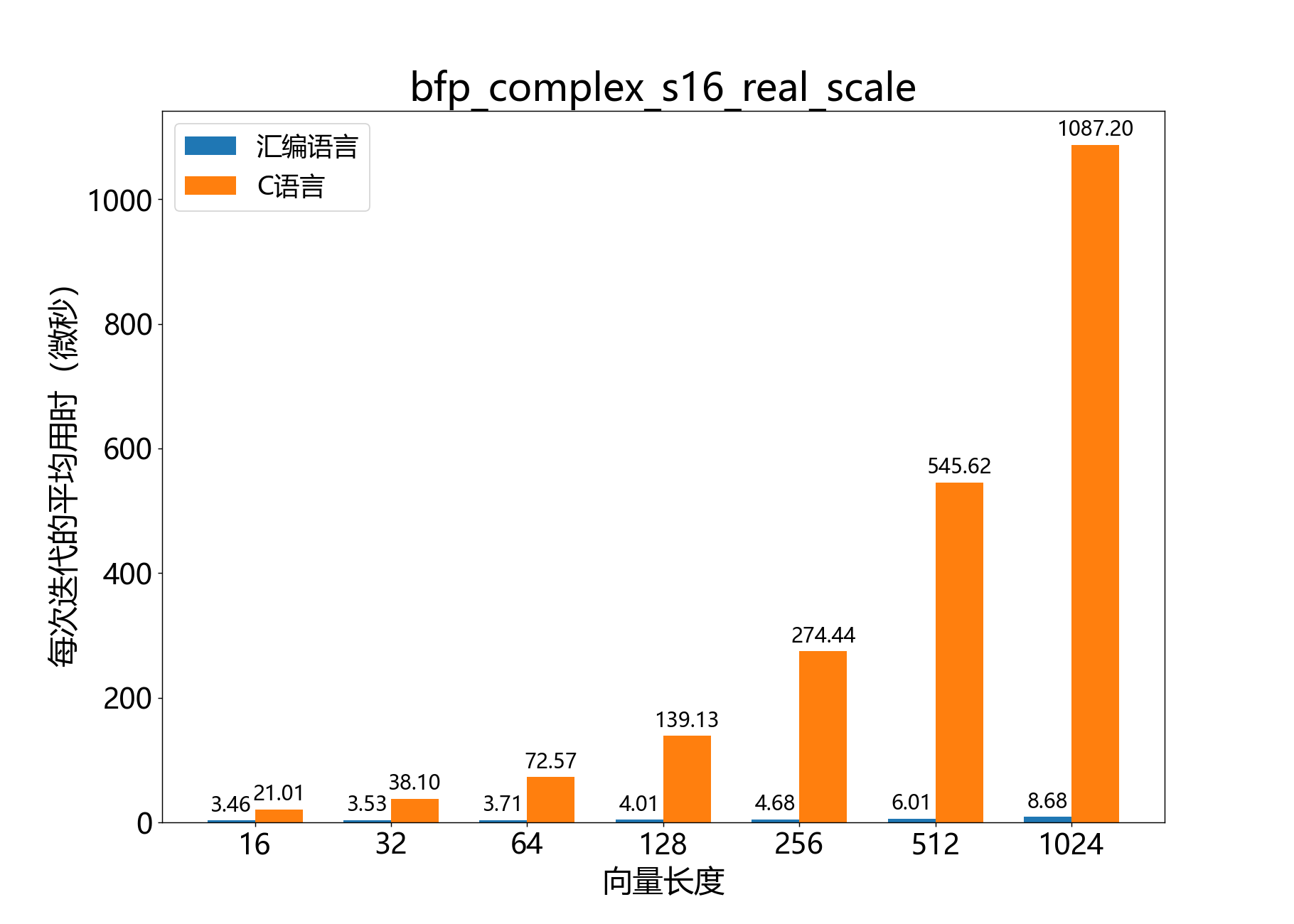
bfp_complex_s16_real_scale

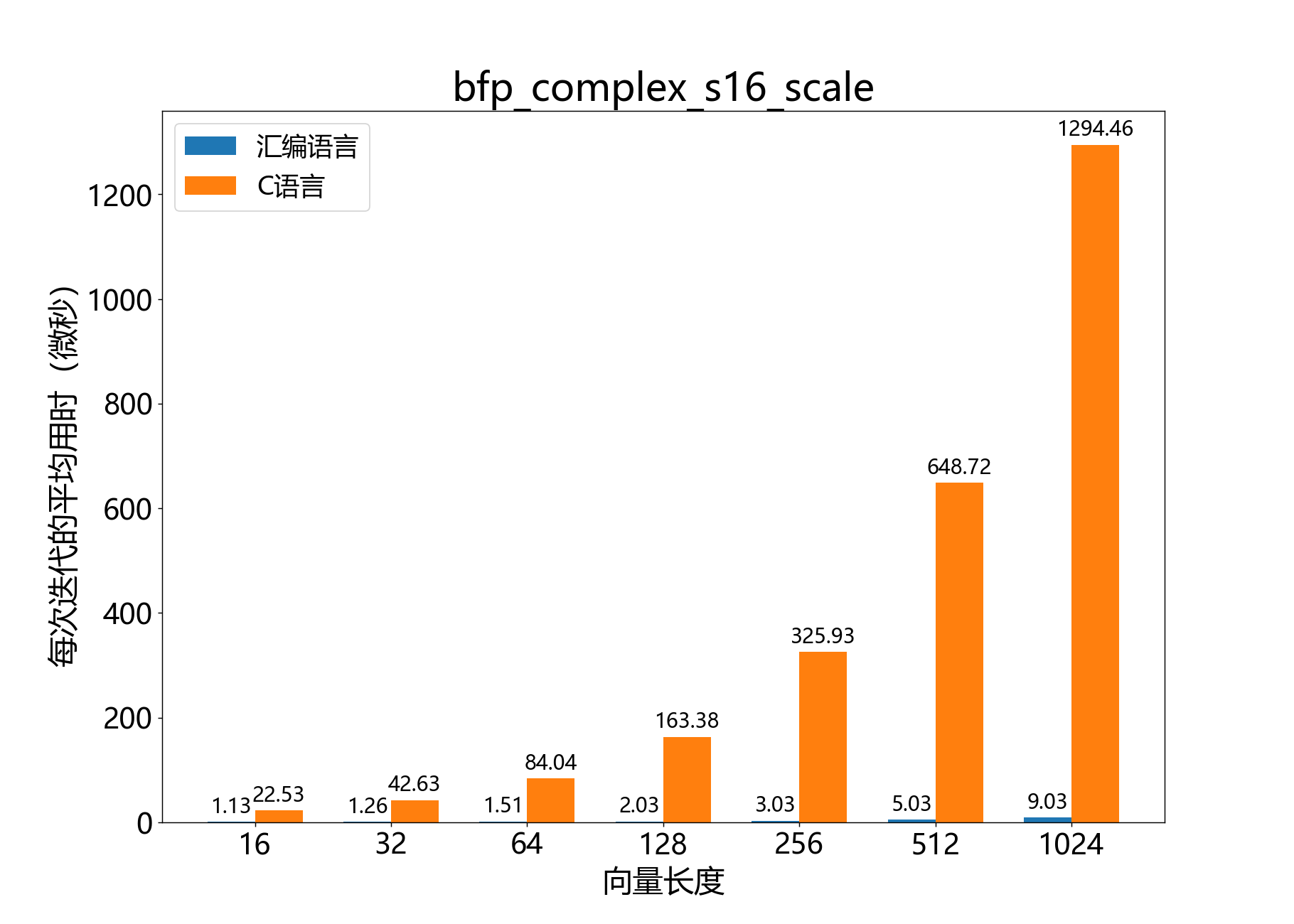
void bfp_complex_s16_scale()​

将一个复数16位BFP向量乘以一个复数标量。

操作：

Aˉ←Bˉ⋅(α⋅2α_exp)\bar{A} \leftarrow \bar{B} \cdot \left( \alpha \cdot 2^{\alpha\_exp} \right)

参数：

  • bfp_complex_s16_t* a – [out] 输出复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const float_complex_s16_t alpha – [in] 乘以 Bˉ\bar{B} 的复数标量 α\alpha

参考性能:

bfp_complex_s16_scale

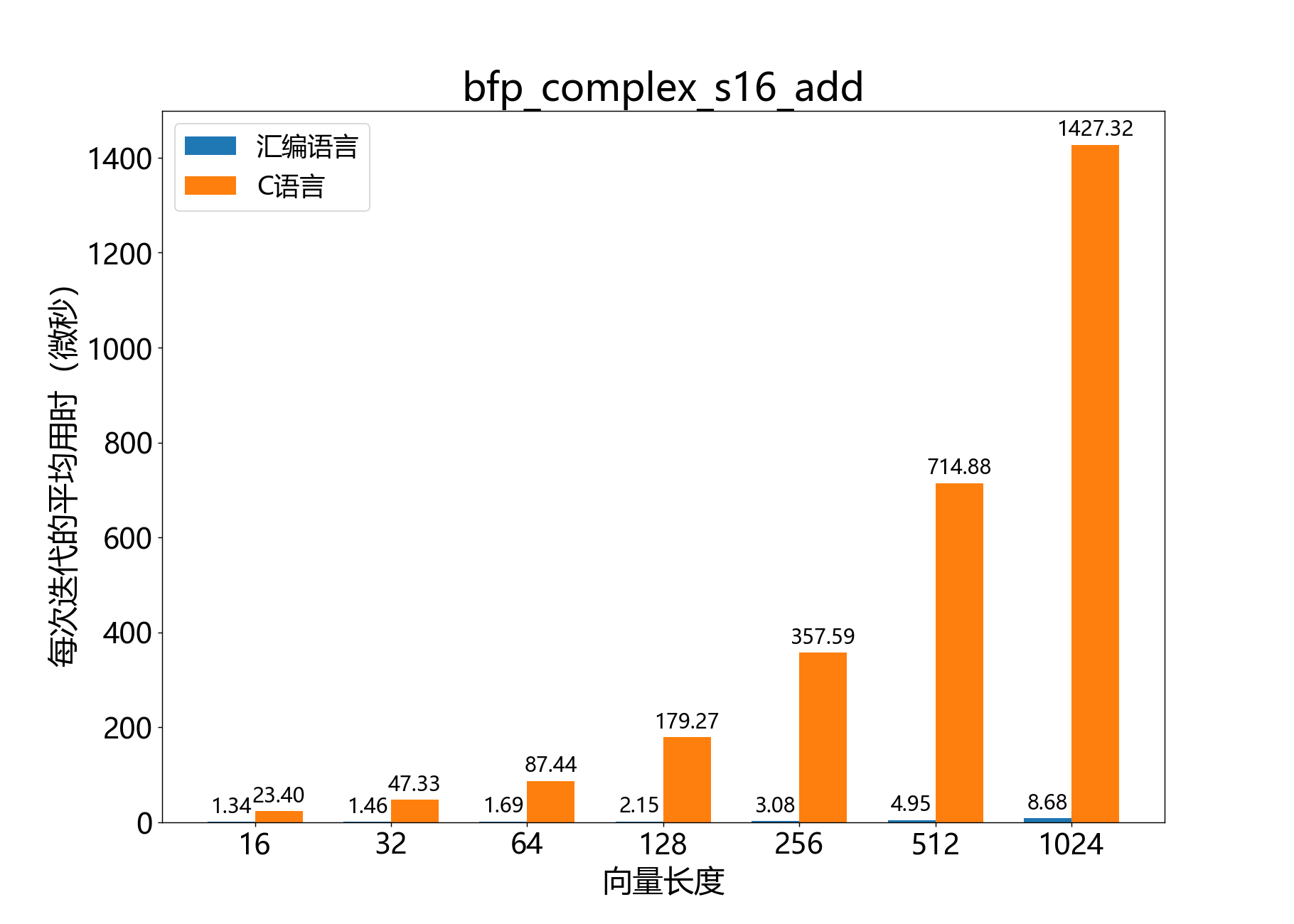
void bfp_complex_s16_add()​

将一个复数16位BFP向量与另一个向量相加。

操作：

Aˉ←Bˉ+Cˉ\bar{A} \leftarrow \bar{B} + \bar{C}

参数：

  • bfp_complex_s16_t* a – [out] 输出复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const bfp_complex_s16_t* c – [in] 输入复数BFP向量 Cˉ\bar{C}

参考性能:

bfp_complex_s16_add

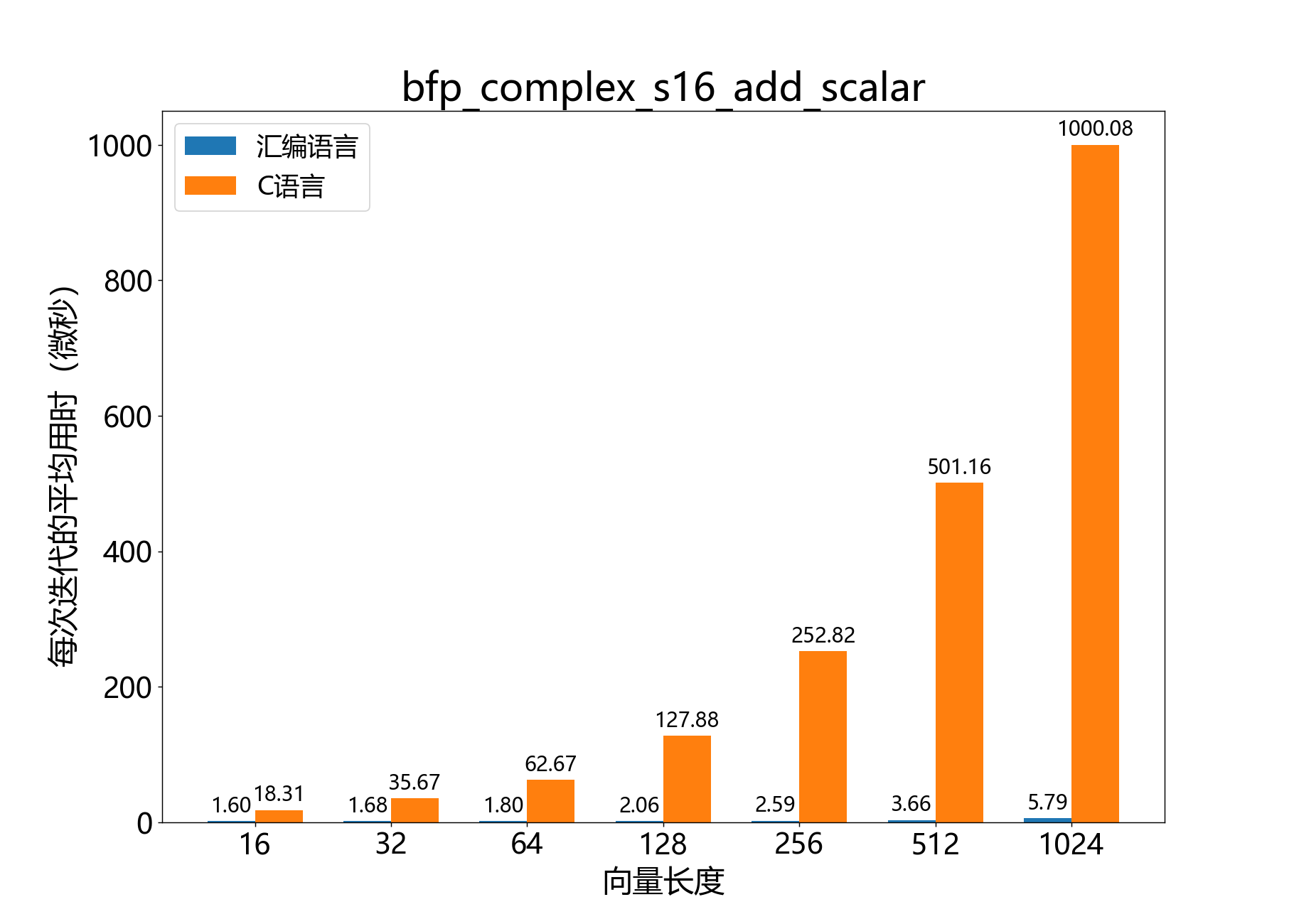
void bfp_complex_s16_add_scalar()​

将一个复数标量加到一个复数16位BFP向量中。

操作：

Aˉ←Bˉ+c\bar{A} \leftarrow \bar{B} + c

参数：

  • bfp_complex_s16_t* a – [out] 输出复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const float_complex_s16_t c – [in] 输入复数标量 cc

参考性能:

bfp_complex_s16_add_scalar

void bfp_complex_s16_sub()​

将一个复数16位BFP向量从另一个向量中减去。

操作：

Aˉ←Bˉ−Cˉ\bar{A} \leftarrow \bar{B} - \bar{C}

参数：

  • bfp_complex_s16_t* a – [out] 输出复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}
  • const bfp_complex_s16_t* c – [in] 输入复数BFP向量 Cˉ\bar{C}

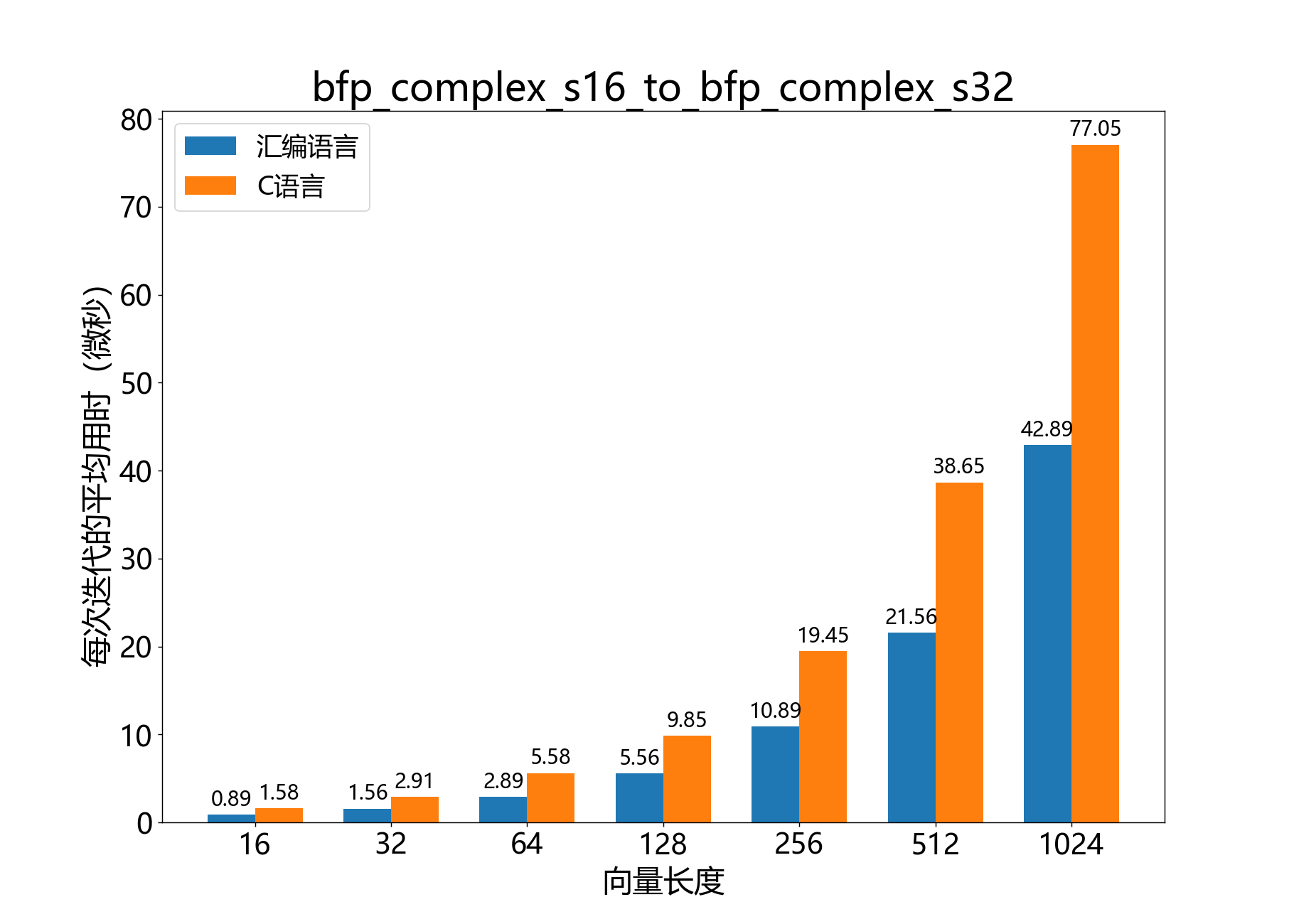
void bfp_complex_s16_to_bfp_complex_s32()​

将一个复数16位BFP向量转换为一个复数32位BFP向量。

操作：

Ak⟵32−bitBk对于 k∈0 ... (N−1)其中 N 是 Bˉ 的长度\begin{align*} A_k &\overset{32-bit}{\longleftarrow} B_k \\ &\text{对于 } k \in 0\ ...\ (N-1) \\ &\text{其中 } N \text{ 是 } \bar{B} \text{ 的长度} \end{align*}

参数：

  • bfp_complex_s32_t* a – [out] 输出复数32位BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数16位BFP向量 Bˉ\bar{B}

参考性能:

bfp_complex_s16_to_bfp_complex_s32

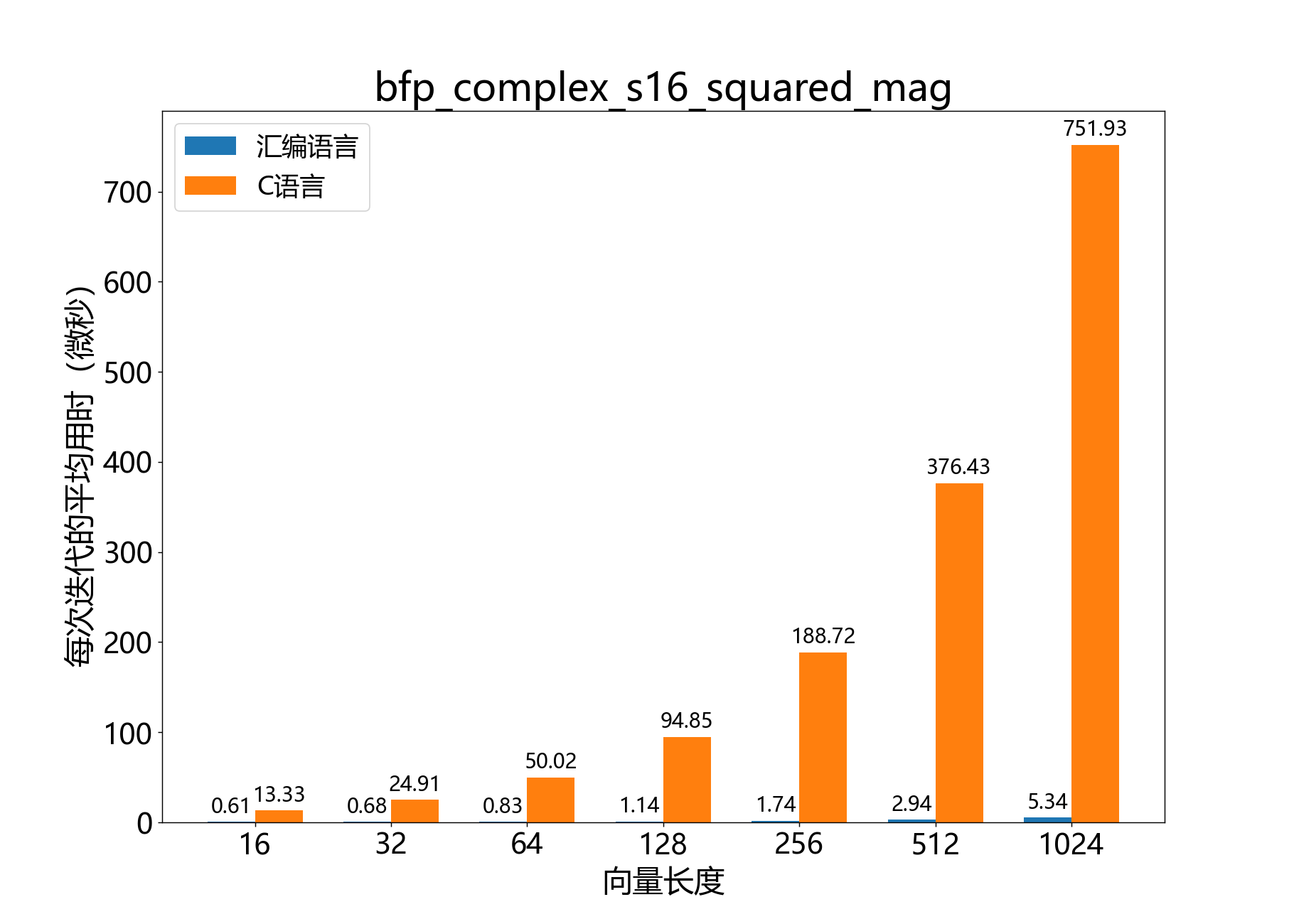
void bfp_complex_s16_squared_mag()​

获取复数16位BFP向量每个元素的平方幅值。

操作：

Ak←Bk⋅(Bk)∗对于 k∈0 ... (N−1)其中 N 是 Bˉ 的长度(Bk)∗ 是 Bk 的复共轭\begin{align*} A_k &\leftarrow B_k \cdot (B_k)^* \\ &\text{对于 } k \in 0\ ...\ (N-1) \\ &\text{其中 } N \text{ 是 } \bar{B} \text{ 的长度} \\ &(B_k)^* \text{ 是 } B_k \text{ 的复共轭} \end{align*}

参数：

  • bfp_s16_t* a – [out] 输出实数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}

参考性能:

bfp_complex_s16_squared_mag

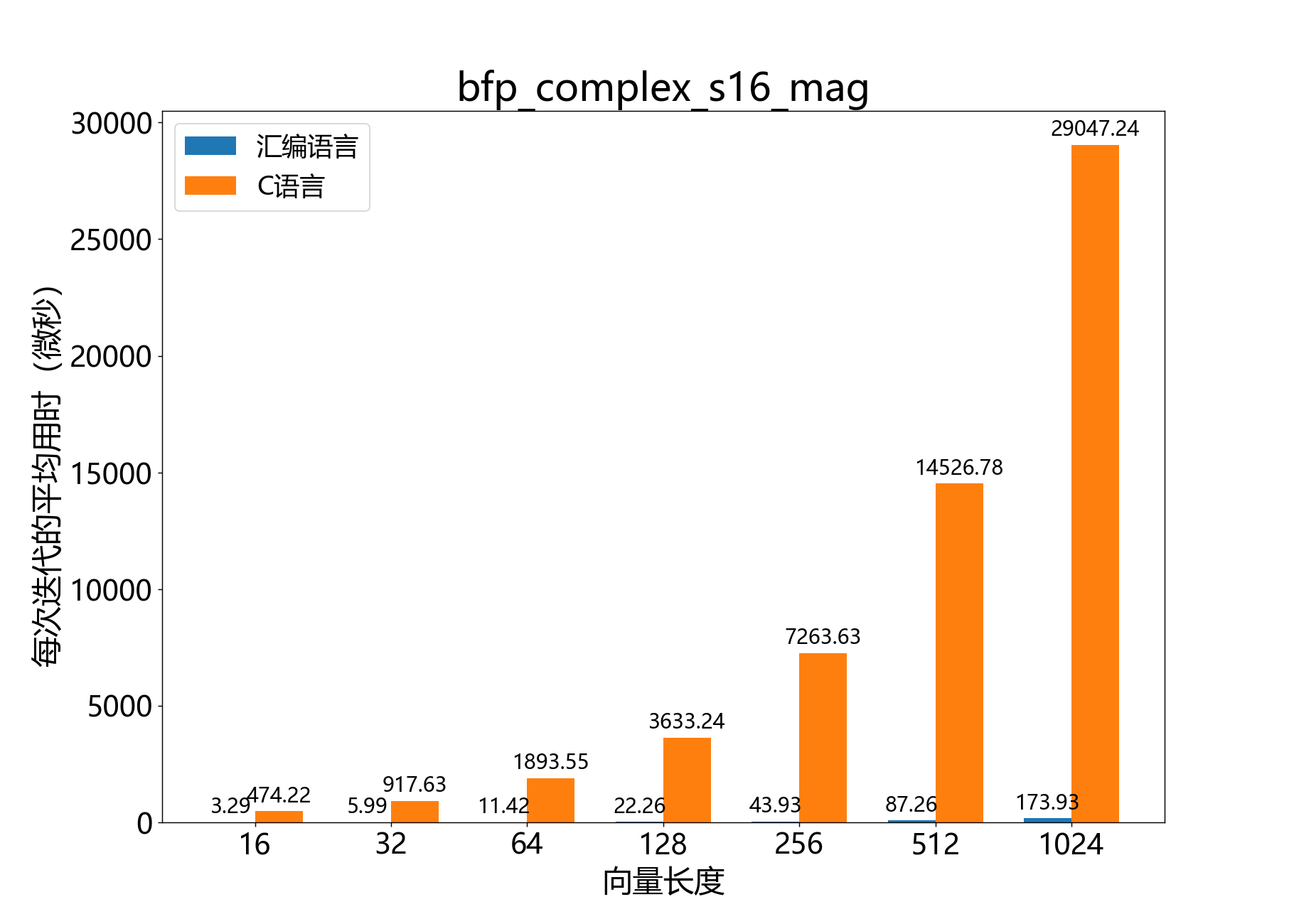
void bfp_complex_s16_mag()​

获取复数16位BFP向量每个元素的幅值。

操作：

Ak←∣Bk∣对于 k∈0 ... (N−1)其中 N 是 Bˉ 的长度\begin{align*} A_k &\leftarrow \left| B_k \right| \\ &\text{对于 } k \in 0\ ...\ (N-1) \\ &\text{其中 } N \text{ 是 } \bar{B} \text{ 的长度} \end{align*}

参数：

  • bfp_s16_t* a – [out] 输出实数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}

参考性能:

bfp_complex_s16_mag

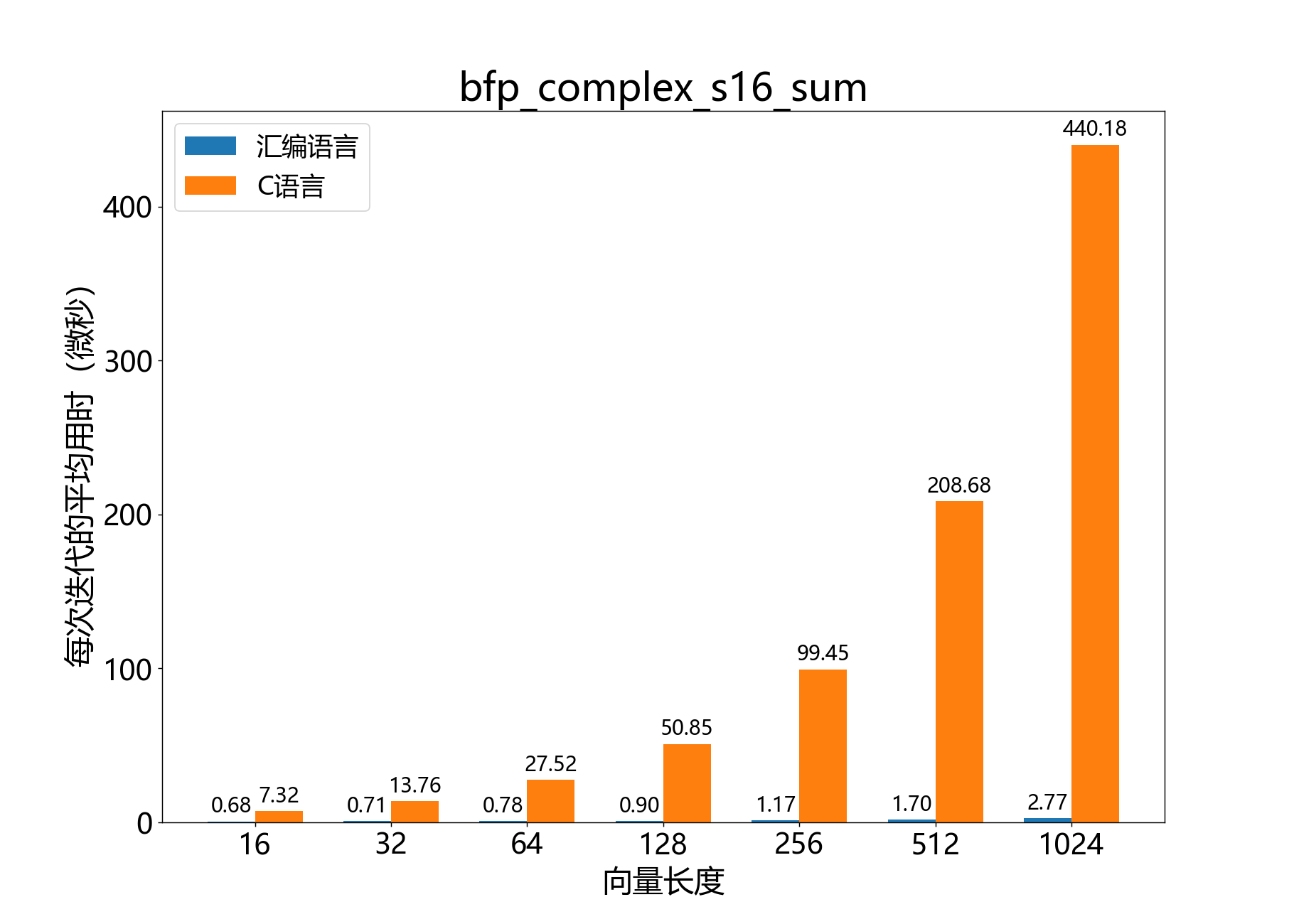
float_complex_s32_t bfp_complex_s16_sum()​

获取复数16位BFP向量的元素之和。

操作：

a←∑k=0N−1(bk⋅2B_exp)对于k∈0 ... (N−1),其中N是Bˉ 的长度。\begin{align*} a &\leftarrow \sum_{k=0}^{N-1} \left( b_k \cdot 2^{B\_exp} \right) \\ &\text{对于} k \in 0\ ...\ (N-1), \\ &\text{其中} N \text{是} \bar{B} \ \text{的长度。} \end{align*}

参数：

  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}

返回值：

  • aa，向量 Bˉ\bar{B} 的元素之和

参考性能:

bfp_complex_s16_sum

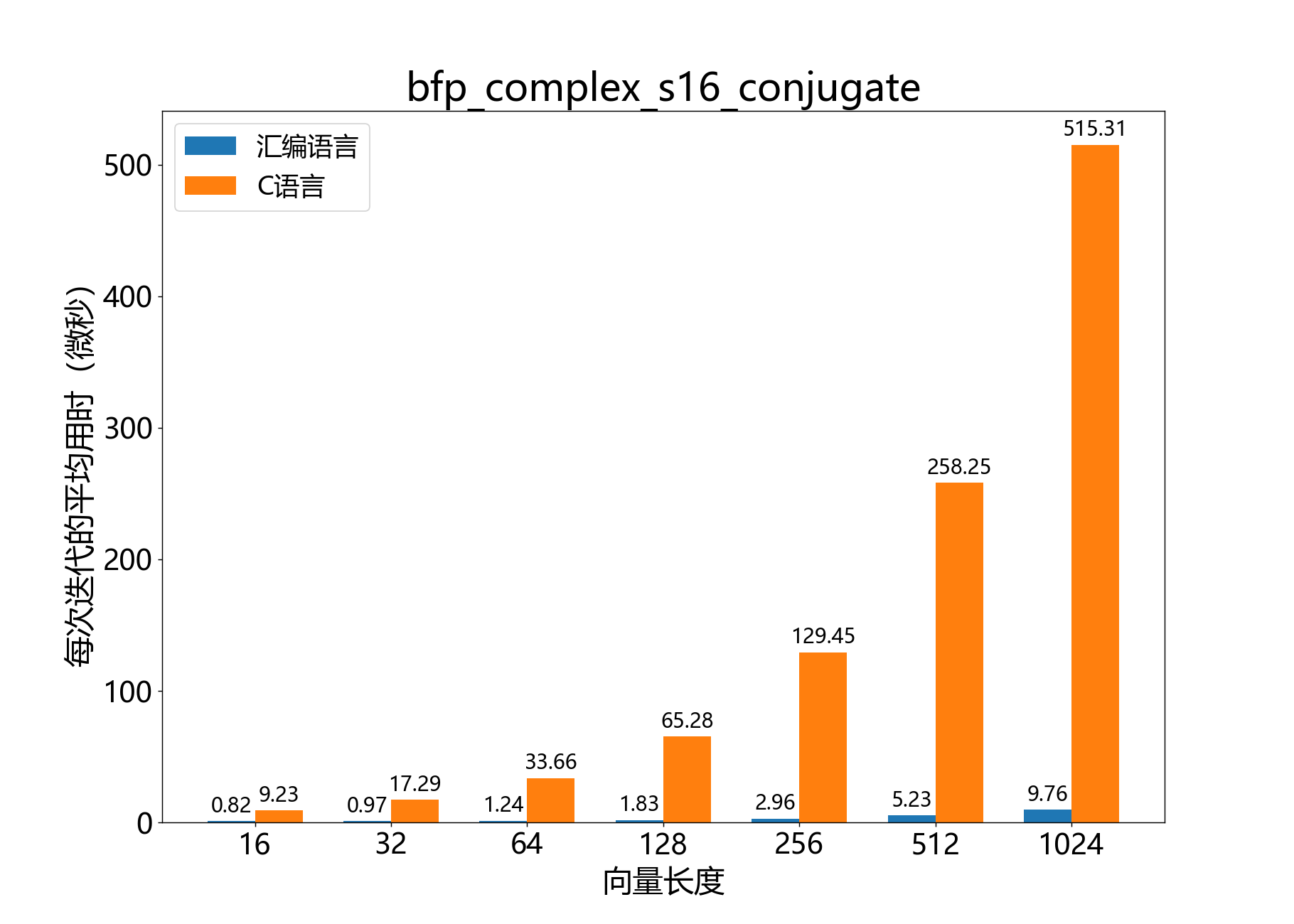
void bfp_complex_s16_conjugate()​

获取复数16位BFP向量每个元素的复共轭。

操作：

Ak←Bk∗对于k∈0 ... (N−1),其中N是Bˉ 的长度。Bk∗是Bk的复共轭。\begin{align*} A_k &\leftarrow B_k^* \\ &\text{对于} k \in 0\ ...\ (N-1), \\ &\text{其中} N \text{是} \bar{B} \ \text{的长度。}\\ &B_k^* \text{是} B_k \text{的复共轭。} \end{align*}

参数：

  • bfp_complex_s16_t* a – [out] 输出复数BFP向量 Aˉ\bar{A}
  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}

参考性能:

bfp_complex_s16_conjugate

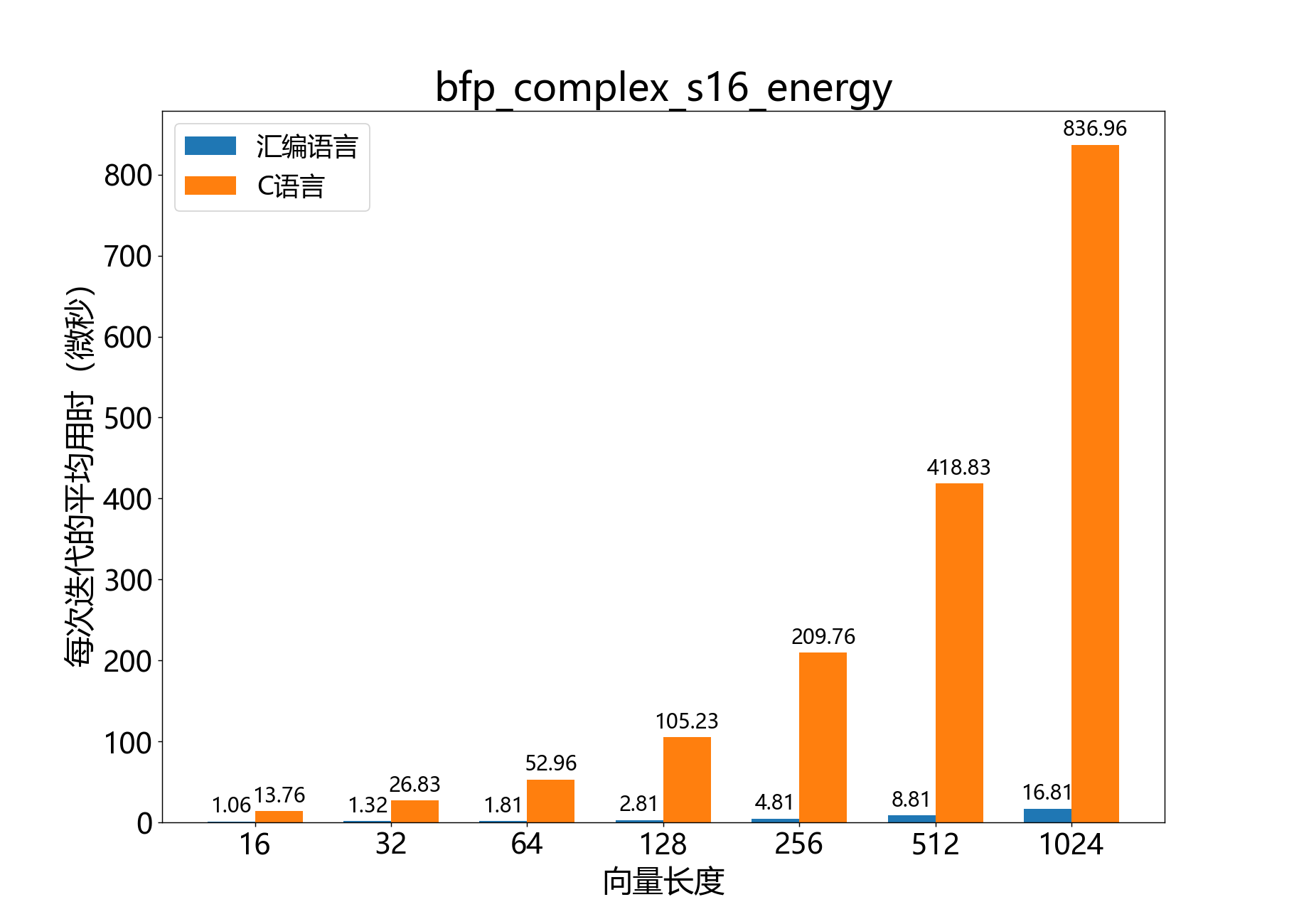
float_s64_t bfp_complex_s16_energy()​

获取复数16位BFP向量的能量。

操作：

a←∑k=0N−1(∣bk⋅2B_exp∣2)对于k∈0 ... (N−1)其中N是Bˉ的长度\begin{align*} a &\leftarrow \sum_{k=0}^{N-1} \left( \left|b_k \cdot 2^{B\_exp}\right|^2 \right) \\ &\text{对于} k \in 0\ ...\ (N-1)\\ &\text{其中} N \text{是} \bar{B} \text{的长度} \end{align*}

参数：

  • const bfp_complex_s16_t* b – [in] 输入复数BFP向量 Bˉ\bar{B}

返回值：

  • aa，向量 Bˉ\bar{B} 的能量

参考性能:

bfp_complex_s16_energy

编辑此页
本文最后由 Vergil Wong 更新于