附录：性能信息

附录：性能信息

本附录提供了与特定感兴趣场景的额外性能信息。这些案例不太适合放在教程的主体部分，但这些信息很可能会有用。从概念角度来讲，这些案例没有进行深入讨论。文档中会提到实现这些案例的代码，但具体的代码分析留给读者自行完成。

用于测量性能的应用程序很小，仅依赖于lib_xcore_math（与第1至4部分的代码没有共享）。

浮点数FIR滤波器，另一种方法

在第1B部分和第1C部分中，我们研究了FIR滤波器的全浮点数实现。本节直接比较了经过优化的全浮点数实现与使用lib_xcore_math的32位数字滤波器API，并使用float包装器将输入从float转换为定点数进行滤波，然后将输出再转换回float的性能。（与第1C部分相反）。

信息

这里使用的“包装”方法仍然对输入和输出样本块进行操作，因为这样可以比逐个样本转换更高效地进行转换。

由于涉及浮点逻辑的代码路径对数据值很敏感，因此使用了随机滤波器权重和输入数据。

本应用程序中创建的滤波器阶数范围从64个抽头到1024个抽头。

FIR结果

以下各节介绍了运行应用程序时的测量结果。在所有情况下，设备的核心时钟频率为600 MHz。

信息

下面图表中的数据是使用xcore内置的100 MHz参考时钟测量的时间。这些测量数据取决于一些细节，包括代码在内存中的放置位置、编译器优化级别等。在实际应用中，性能可能会有所不同。

特别是，我发现在filter_wrapped.c文件中对filter_wrapped()函数进行相对较小的更改可能会导致性能有几个百分点的差异。

样本处理性能

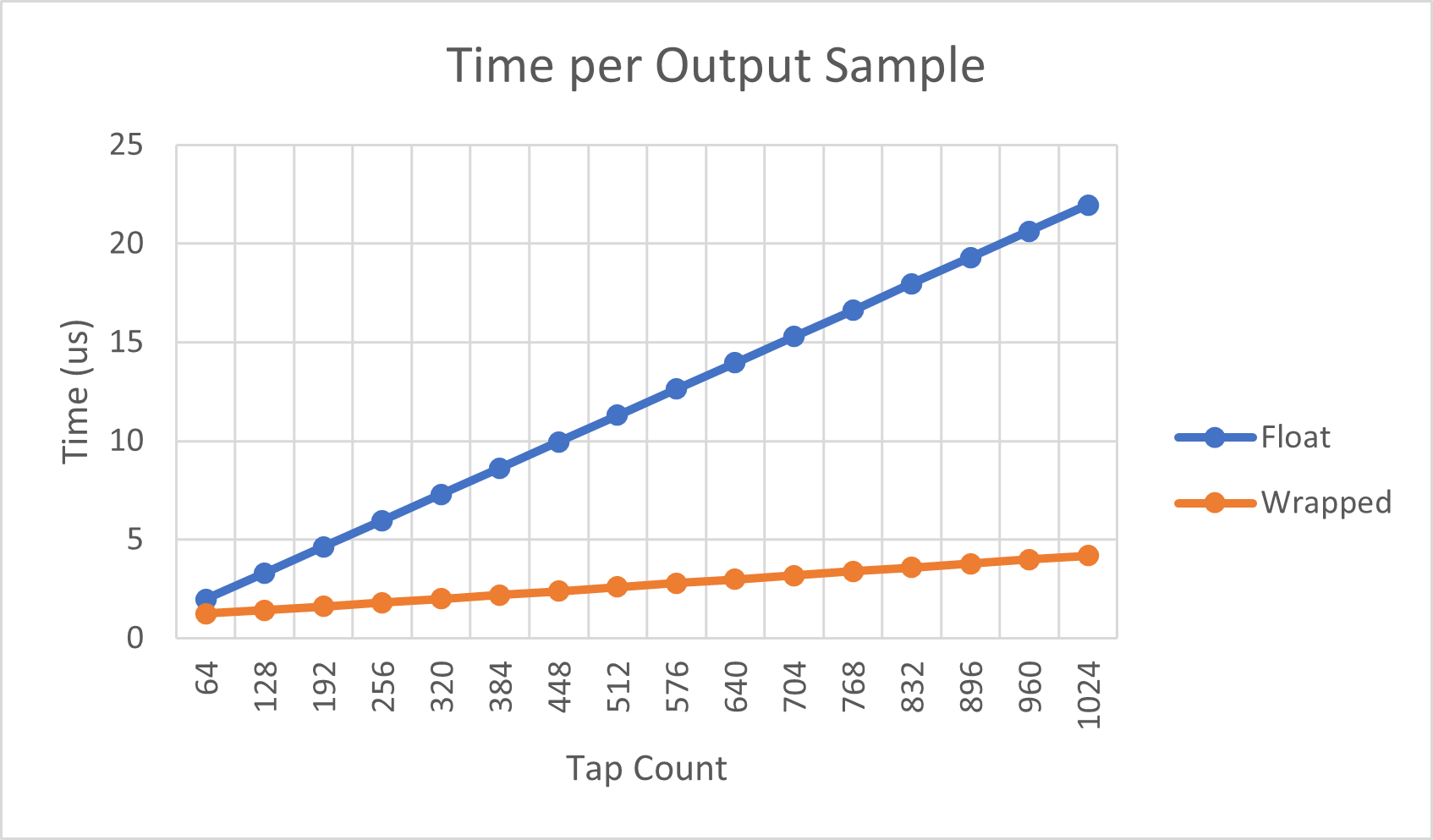
上图比较了每种实现的每个输出样本处理时间（以微秒为单位）与抽头数的关系。"Float"系列是纯浮点数实现，"Wrapped"是使用浮点数包装器的定点数FIR滤波器。如预期的那样，两种实现的时间成本都与抽头数线性增加。纯浮点数实现的每个滤波器抽头的成本增加得更快。

根据计算每个输出样本的时间，我们可以取其倒数，得到每种实现在实时系统中能够处理的最大样本率。

信息

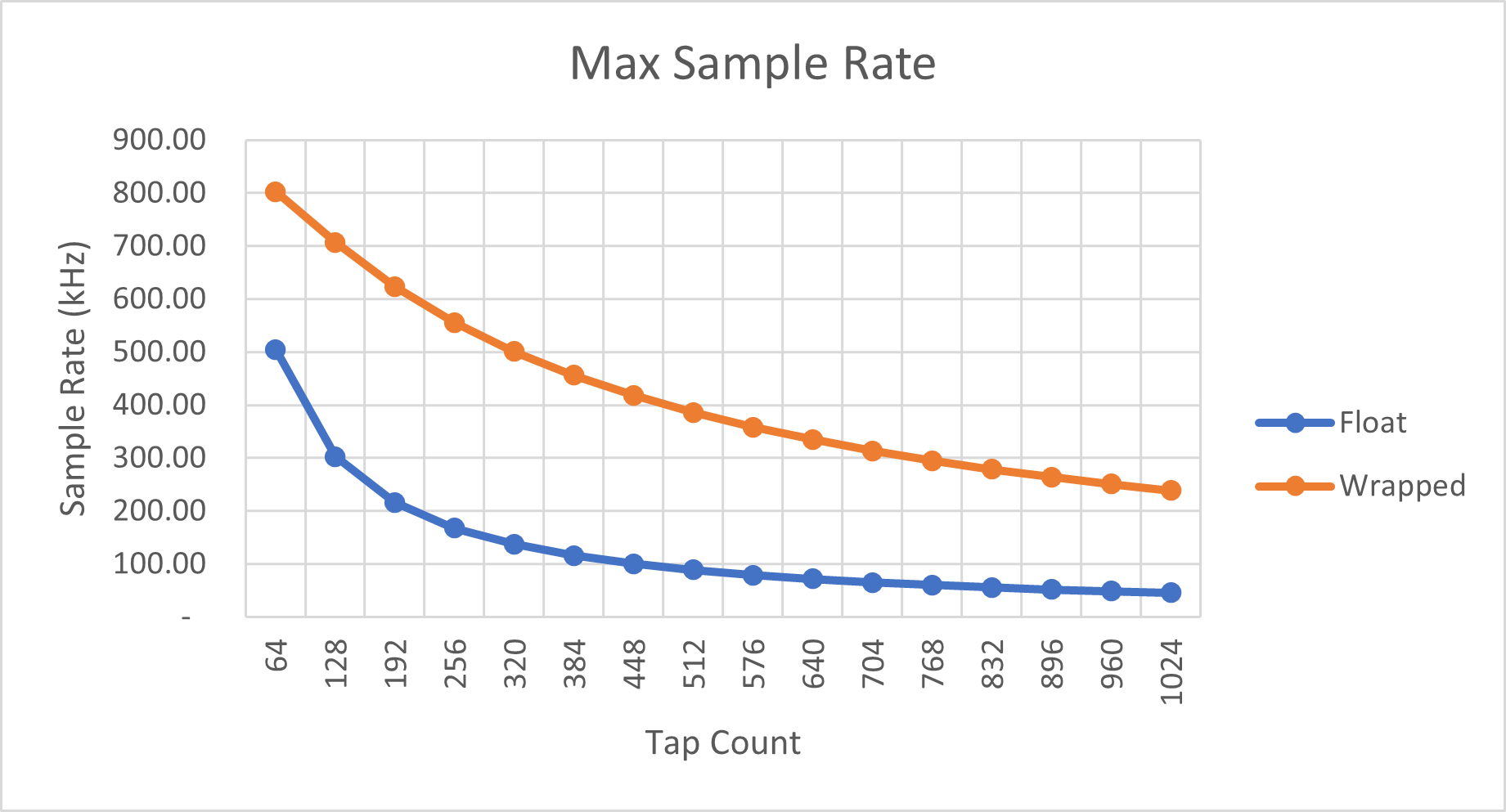
这里描述的最大样本率假设只使用单个线程来处理实时输入流的滤波。通过使用多个硬件核心或 Tile ，仍然可以处理更高的实时样本率。

当抽头数增加时，最大样本率自然会降低。然而，由于随着抽头数增加，包装实现变得相对更高效，对于较大的滤波器来说，它可以处理比浮点数实现更高的样本率。

下图显示了"Float"样本时间与"Wrapped"样本时间的比值，更明确地进行了比较。

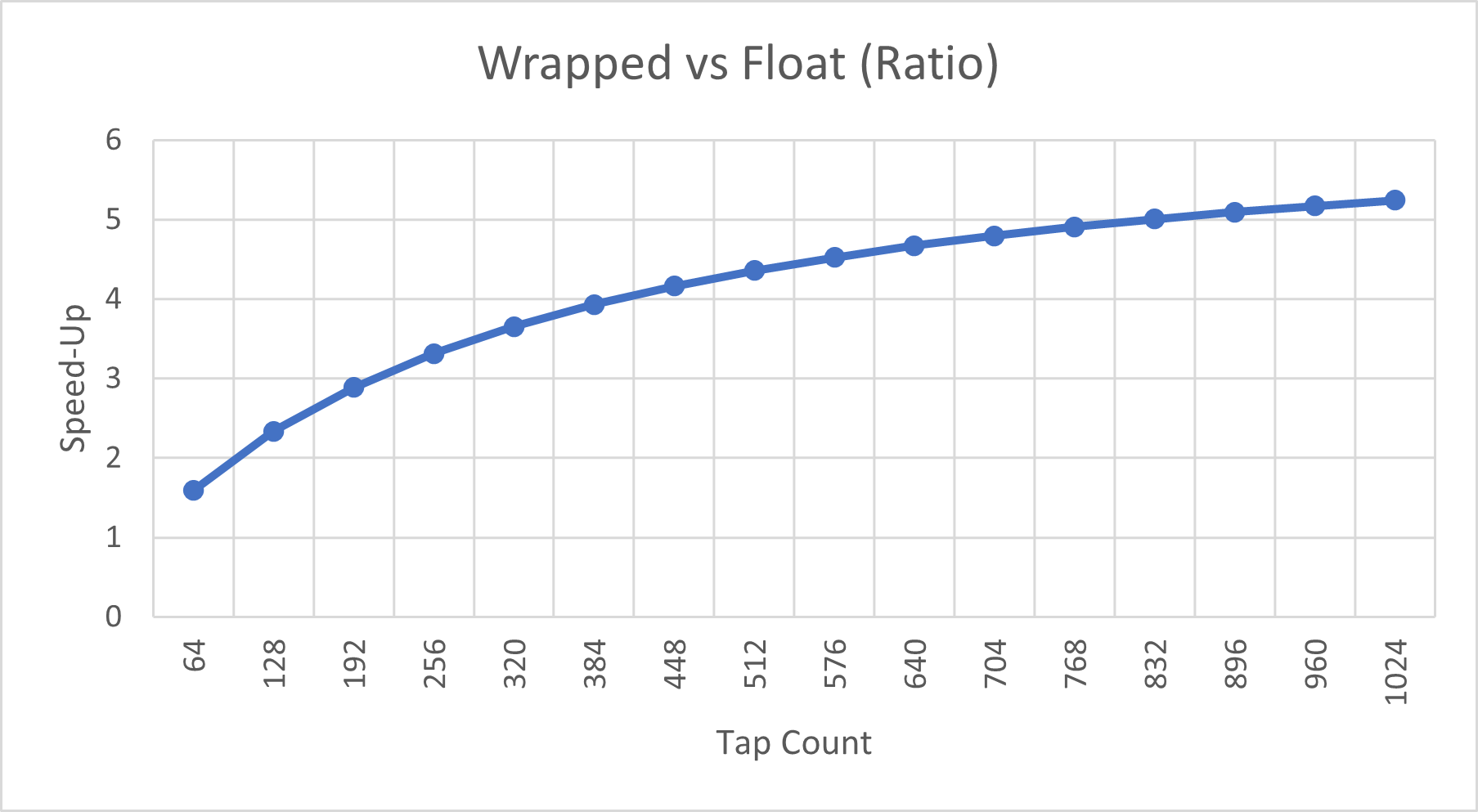
累加速率

下图比较了浮点数和包装实现的累加速率。这里的"累加速率"定义为每秒发生的（有用的）等效标量乘-加操作的数量。这里的"有用"仅包括计算输出样本所需的乘-加操作。例如，一个128抽头的FIR滤波器每个输出样本恰好有128个"有用"的乘-加操作。

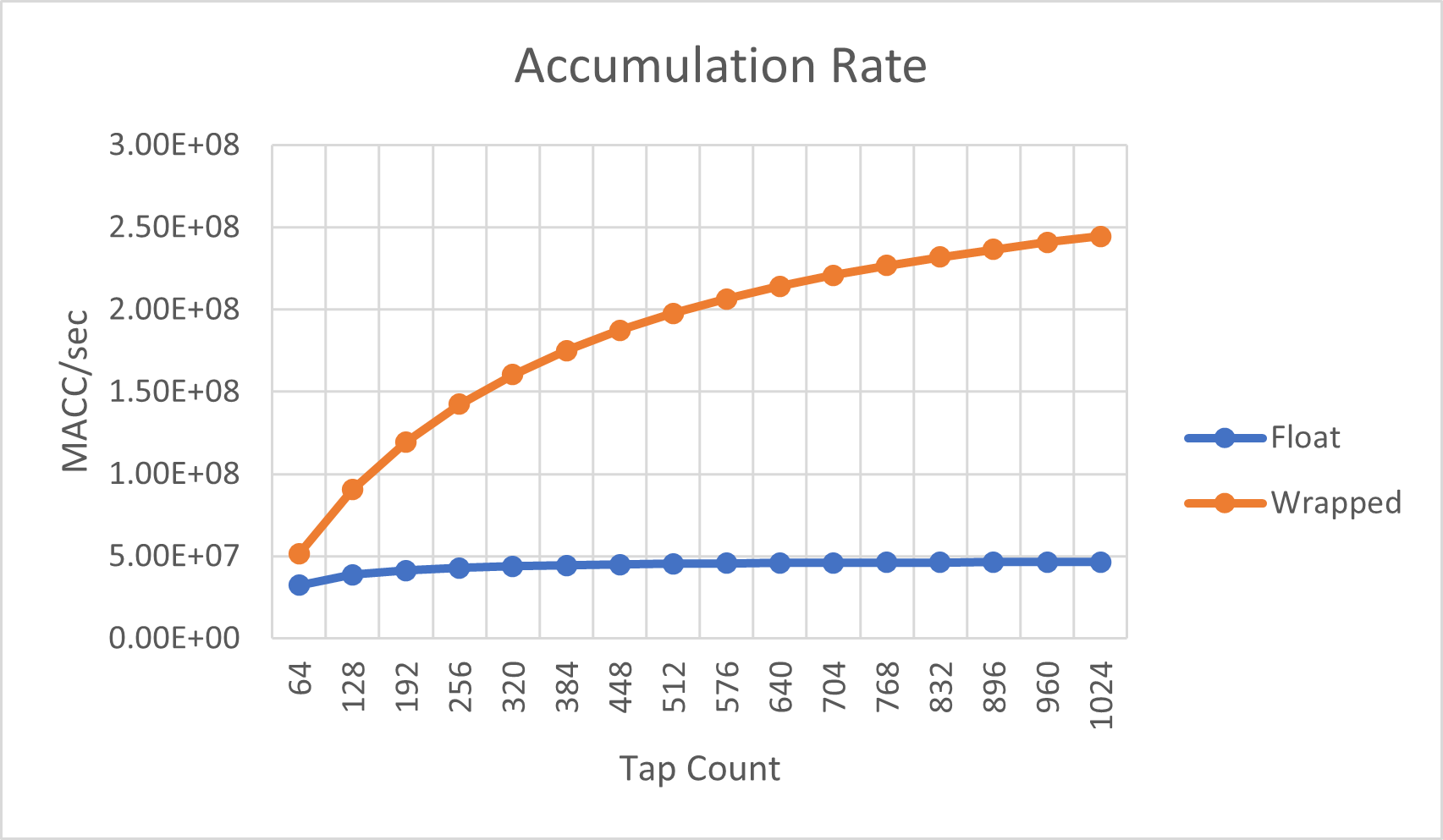
在Float和Wrapped实现之间，我们可以看到性能上的重大差异。每个实现都使用了lib_xcore_math库函数，内部循环针对大型滤波器进行了优化。但是，每个实现在优化循环之外还有一些固定的开销。

浮点数滤波器实现的开销相对较小，这就是为什么其累加速率从64个抽头的约32.3 MMACCs/秒增加到1024个抽头的约46.7 MMACCs/秒。另一方面，包装实现可以处理约51.4 MMACCs/秒的64个抽头，而在1024个抽头时则增加到约245 MMACCs/秒。这就是为什么包装实现在处理较大的滤波器时效率更高的原因。

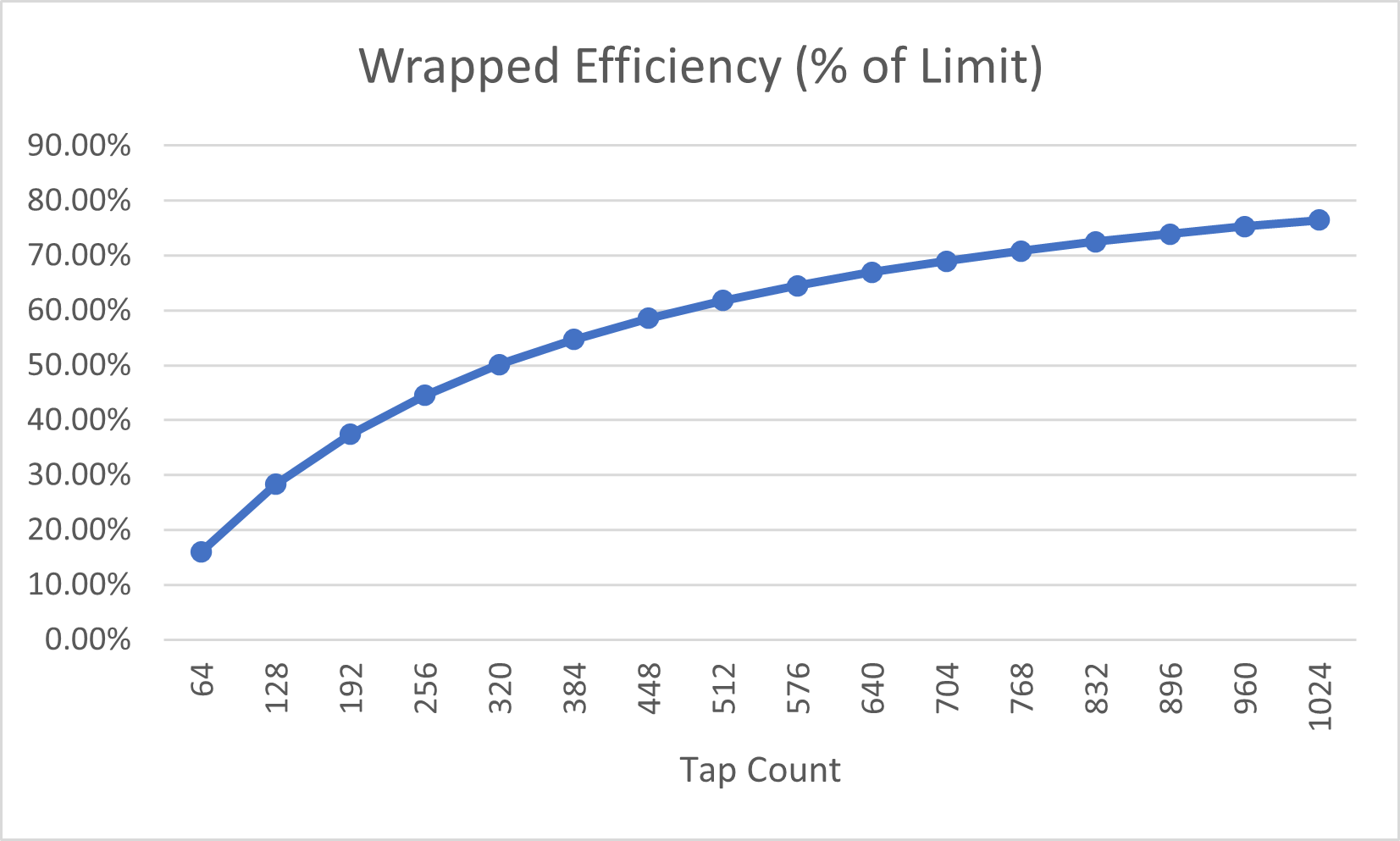
最后一个图表显示了包装实现的效率与抽头数的关系。这里的效率是累加速率除以随着抽头数增加趋近于无穷大时的累加速率。

累加速率的理论极限是滤波器在内部循环中花费100%的时间时达到的速率。因此，它是几个因素的函数：$F$，核心CPU时钟频率；$I$，内部循环指令数（或在双发射（dual-issue）模式下的指令束数）；$M$，每次循环迭代中执行的MACC数。

$$\begin{aligned} F &= 600 \text{ MHz} \\ M &= 8 \text{ MACC} \\ I &= 3 \text{ Inst} \\ r^* &= \frac{F}{5 \text{ Inst}^{-1}} \cdot \frac{M}{I} \\ &= \frac{600 \text{ MHz}}{5 \text{ Inst}^{-1}} \cdot \frac{8 \text{ MACC}}{3 \text{ Inst}} \\ &= 120 \text{ (MInst/s)} \cdot \frac{8}{3} \text{ (MACC/Inst)} \\ &= 3.2 \cdot 10^8 \text{ MACC/s} \end{aligned}$$

除以5是因为核心流水线有5个阶段，因此单个硬件线程每5个核心时钟周期才能发出一次指令。

快速傅里叶变换

本节比较了各种快速傅里叶变换（FFT）操作的三个版本。其中一种方案是纯浮点数实现。另一种与前一节类似，使用float API，但在内部将浮点数向量转换为BFP，使用BFP进行FFT，然后将结果的BFP向量转换回浮点数。这被称为“包装”实现，因为它是BFP在浮点数API中的“包装”。最后一个版本是纯BFP实现（使用BFP API）。

对于每种方案，测量的操作包括正向实数FFT、反向实数FFT、正向复数FFT和反向复数FFT。每个操作使用长度为$16, 32, 64, 128, 256, 512$和$1024$的输入序列进行测量。

FFT结果

所有结果是在单个硬件线程上运行，核心时钟频率为600MHz。

实数FFT

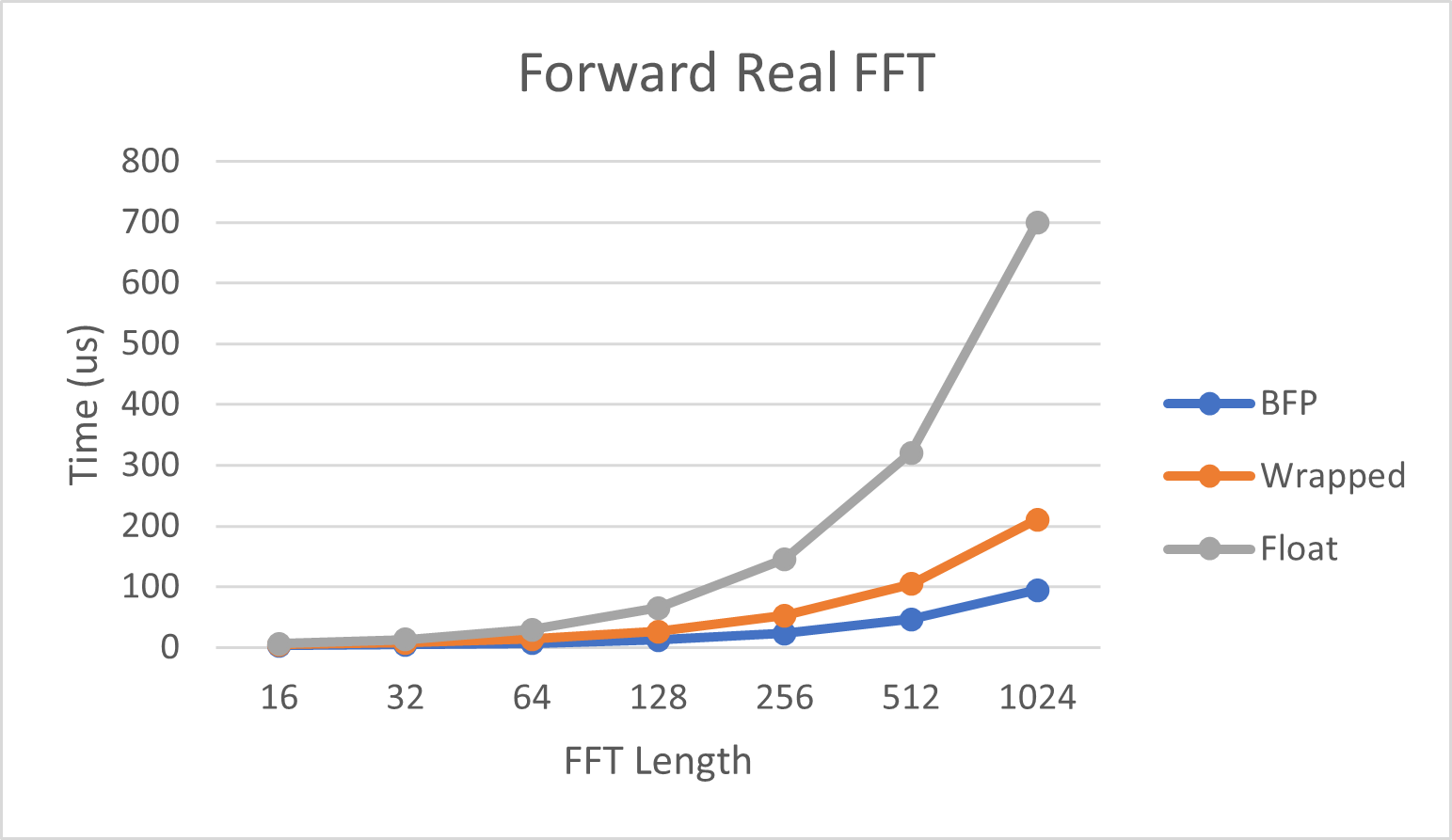
下图显示了执行正向实数FFT所需的时间。实数FFT是单个实值信号的FFT。FFT的特性使得可以使用一个$N$点复数FFT计算一个实值信号的$2N$点FFT，从而加快计算速度。

长度	BFP	Wrapped	Float
16	2.28 us	4.61 us	6.22 us
32	4.29 us	7.89 us	13.67 us
64	6.84 us	14.06 us	30.14 us
128	12.24 us	26.73 us	66.74 us
256	23.31 us	52.34 us	147.1 us
512	46.58 us	104.77 us	323.1 us
1024	94.64 us	210.89 us	705.0 us

实数iFFT

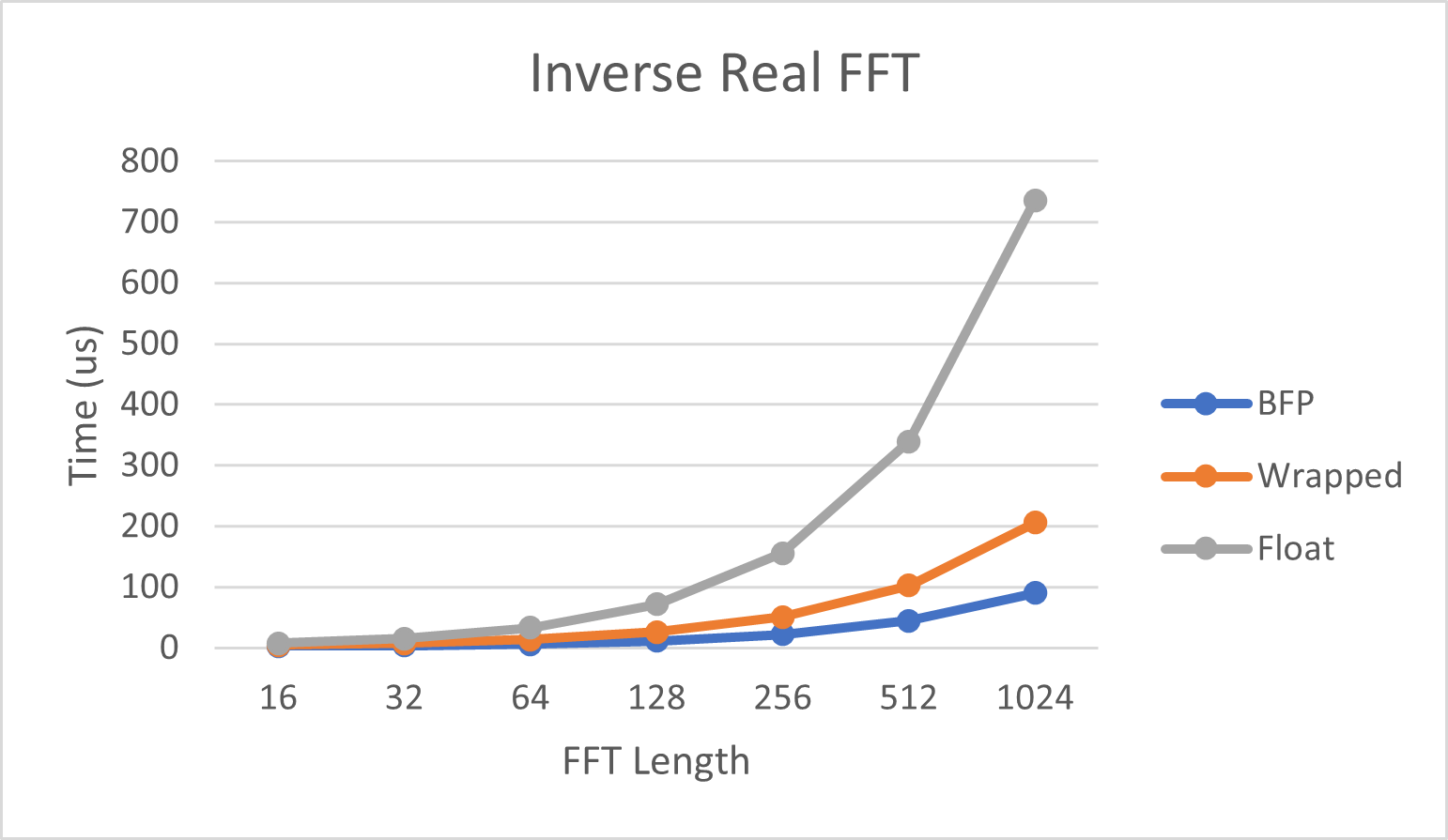
下图显示了执行反向实数FFT所需的时间。实数iFFT是单个实值信号的逆FFT。FFT的特性使得可以使用一个$N$点复数逆FFT计算一个实值$2N$点信号的逆FFT，从而加快计算速度。

长度	BFP	Wrapped	Float
16	2.64 us	4.61 us	7.47 us
32	4.03 us	7.81 us	15.46 us
64	6.44 us	13.88 us	32.97 us
128	11.57 us	26.23 us	71.58 us
256	22.11 us	51.12 us	155.85 us
512	44.31 us	102.39 us	339.33 us
1024	90.24 us	205.80 us	735.60 us

复数FFT

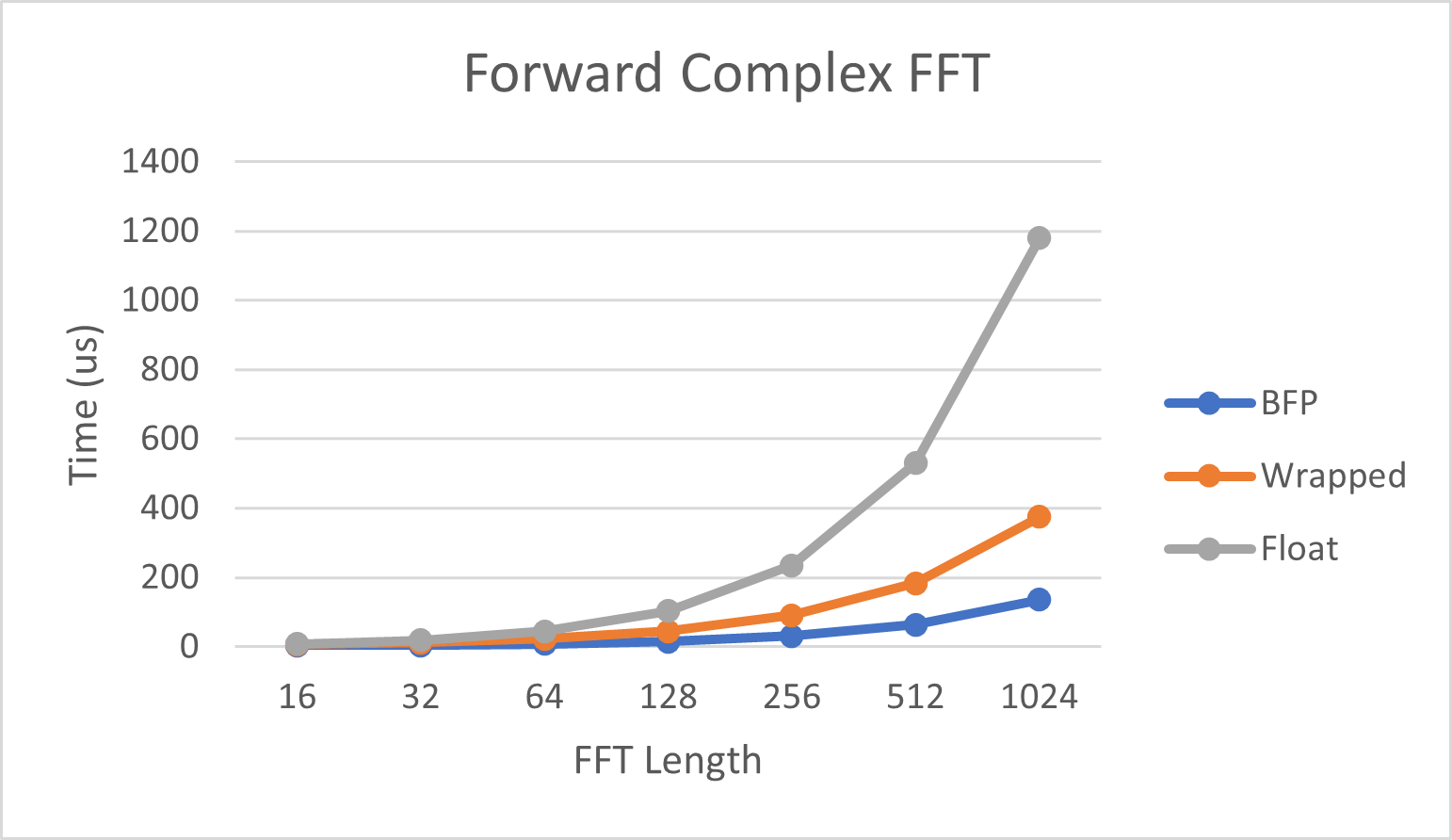
下图显示了执行正向复数FFT所需的时间。

长度	BFP	Wrapped	Float
16	2.34 us	6.23 us	8.17 us
32	3.98 us	11.61 us	19.17 us
64	7.54 us	22.65 us	44.83 us
128	14.94 us	44.97 us	103.37 us
256	30.87 us	90.73 us	235.63 us
512	64.28 us	183.79 us	530.03 us
1024	135.27 us	374.56 us	1179.90 us

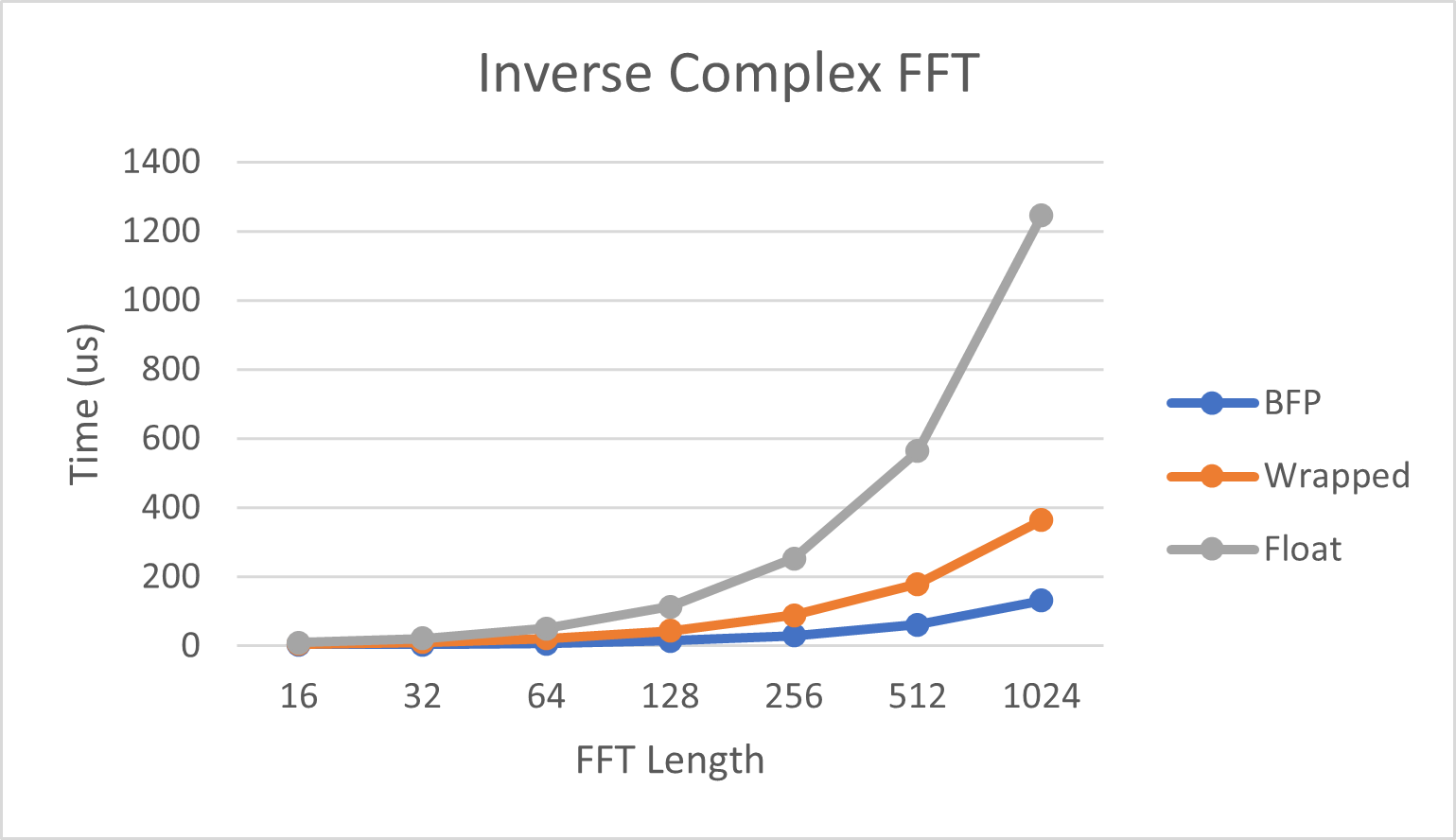
复数iFFT

下图显示了执行反向复数FFT所需的时间。

长度	BFP	Wrapped	Float
16	2.24 us	6.12 us	9.90 us
32	3.81 us	11.38 us	21.87 us
64	7.43 us	22.10 us	49.41 us
128	14.54 us	43.80 us	111.56 us
256	30.36 us	88.48 us	250.77 us
512	61.55 us	178.89 us	558.51 us
1024	130.98 us	364.71 us	1233.98 us