32-Bit Vector Chunk (8-Element) API
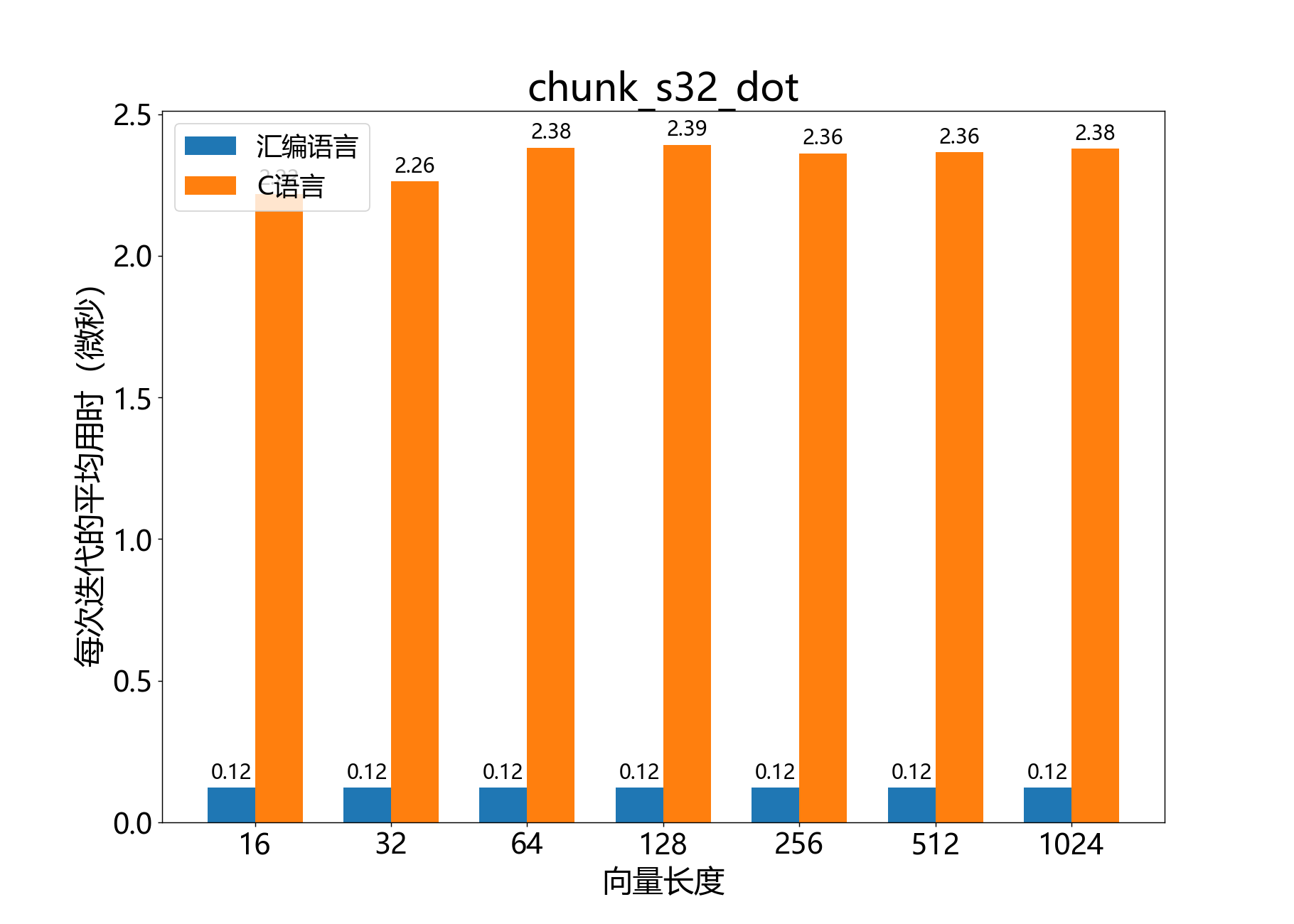
int32_t chunk_s32_dot()
计算两个向量块的内积。
该函数计算向量块 bˉ 和 cˉ 的内积。
从概念上讲,bˉ 的元素可以具有任意数量的小数位(整数、定点数、BFP向量的尾数),只要它们都是相同的。cˉ 的元素是Q2.30的定点数值。返回的值 a 的小数位数与 bˉ 相同。
仅返回和的最低32位。
操作:
a←k=0∑VPU_INT32_EPV−1(round(230bk⋅ck))
参数:
const int32_t b[VPU_INT32_EPV] – [in] 输入块 bˉconst q2_30 c[VPU_INT32_EPV] – [in] 输入块 cˉ
返回值: a
参考性能:
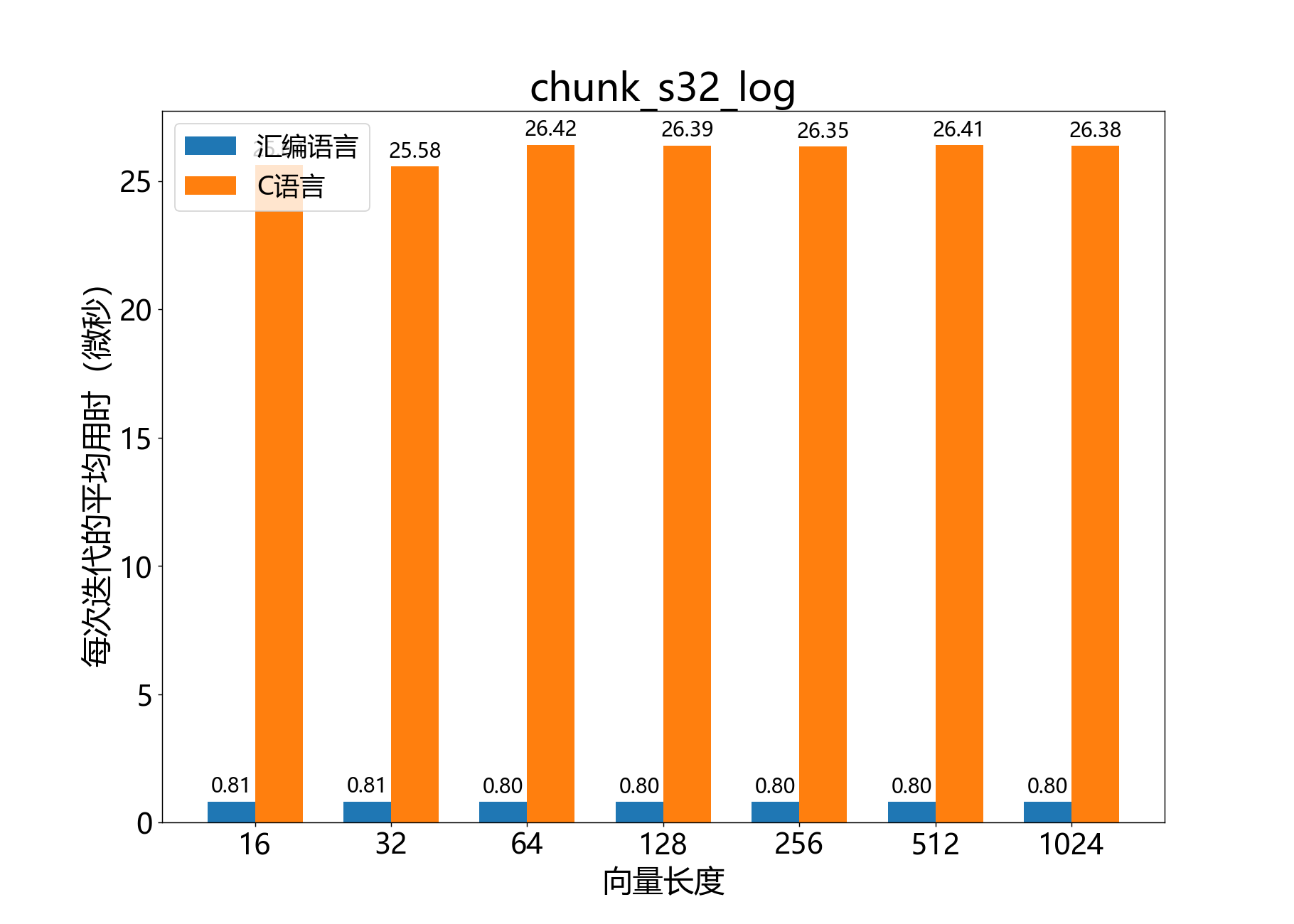
void chunk_s32_log()
计算32位值的向量块的自然对数。
该函数计算向量块 bˉ 中的每个元素的自然对数。结果以Q8.24值的8个元素块 aˉ 形式返回。
b\_exp 是与 bˉ 元素关联的指数。
任何输入 bk≤0 将导致相应的输出 ak=INT32_MIN。
操作:
ak←{log(bk⋅2b_exp)INT32_MINbk>0否则其中 k∈{0..VPU_INT32_EPV−1}
参数:
q8_24 a[VPU_INT32_EPV] – [out] 输出向量块 aˉconst int32_t b[VPU_INT32_EPV] – [in] 输入向量块 bˉconst exponent_t b_exp – [in] 与 bˉ 关联的指数
异常: 如果 b 或 a 不是双字对齐的,则引发 ET_LOAD_STORE 异常。
参考性能:
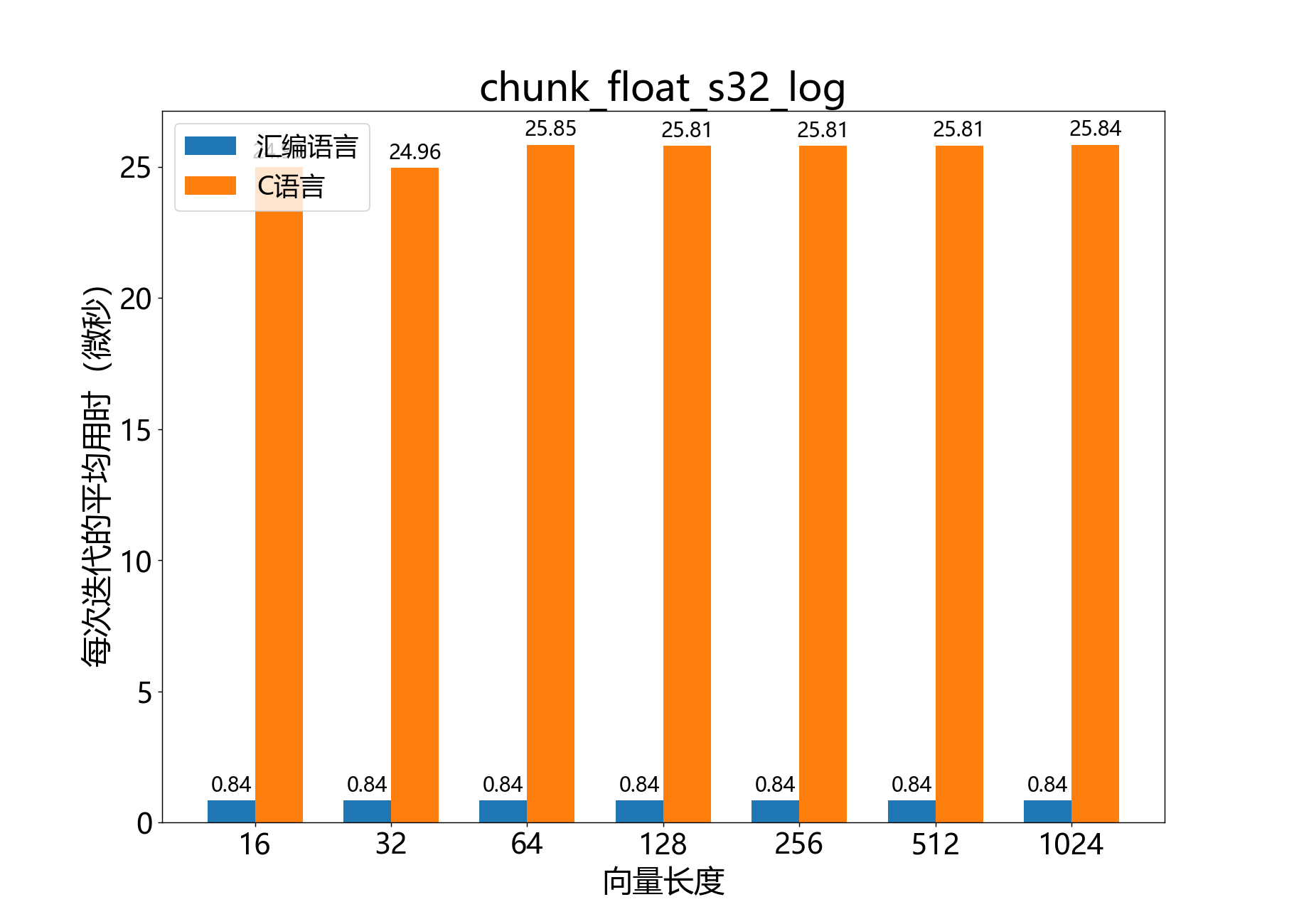
void chunk_float_s32_log()
计算 float_s32_t 向量块的自然对数。
该函数计算向量块 bˉ 中的每个 VPU_INT32_EPV 元素的自然对数。结果以Q8.24值的8个元素块 aˉ 形式返回。
任何输入 bk≤0 将导致相应的输出 ak=INT32_MIN。
操作:
ak←{log(bk)INT32_MINbk>0否则其中 k∈{0..VPU_INT32_EPV−1}
参数:
q8_24 a[VPU_INT32_EPV] – [out] 输出向量块 aˉconst float_s32_t b[VPU_INT32_EPV] – [in] 输入向量块 bˉ
异常: 如果 b 或 a 不是双字对齐的,则引发 ET_LOAD_STORE 异常。
参考性能:
void chunk_q30_power_series()
在Q2.30值的向量块上计算幂级数。
该函数用于计算向量块(VPU_INT32_EPV 元素向量) bˉ 的幂级数求和。bˉ 包含Q2.30值。cˉ 是一个包含要与 bˉ 的幂相乘的系数的向量,并且可以具有任何关联的指数。输出是向量块 aˉ,其指数与 cˉ 相同。
c[] 是一个形状为 (term_count, VPU_INT32_EPV) 的数组,其中第二个轴上的值在所有 VPU_INT32_EPV 元素中都是相同的。也就是说,对于性能原因,c[k][i] = c[k][j] 对于 i 和 j 在 0..(VPU_INT32_EPV-1)。这是为了性能而做的简化。(为了说明问题,cˉ 被认为是单维的,没有冗余。)
操作:
bk,0bk,iak=230=round(230bk,i−1⋅bk)for i∈{1..(N−1)}=i=0∑N−1round(230bk,i⋅ci)for k∈{0..VPU_INT32_EPV−1}
参数:
int32_t a[VPU_INT32_EPV] – [out] 输出向量块 aˉconst q2_30 b[VPU_INT32_EPV] – [in] 输入向量块 bˉconst int32_t c[] – [in] 系数向量 cˉconst unsigned term_count – [in] 幂级数项的数量 N
参考性能:
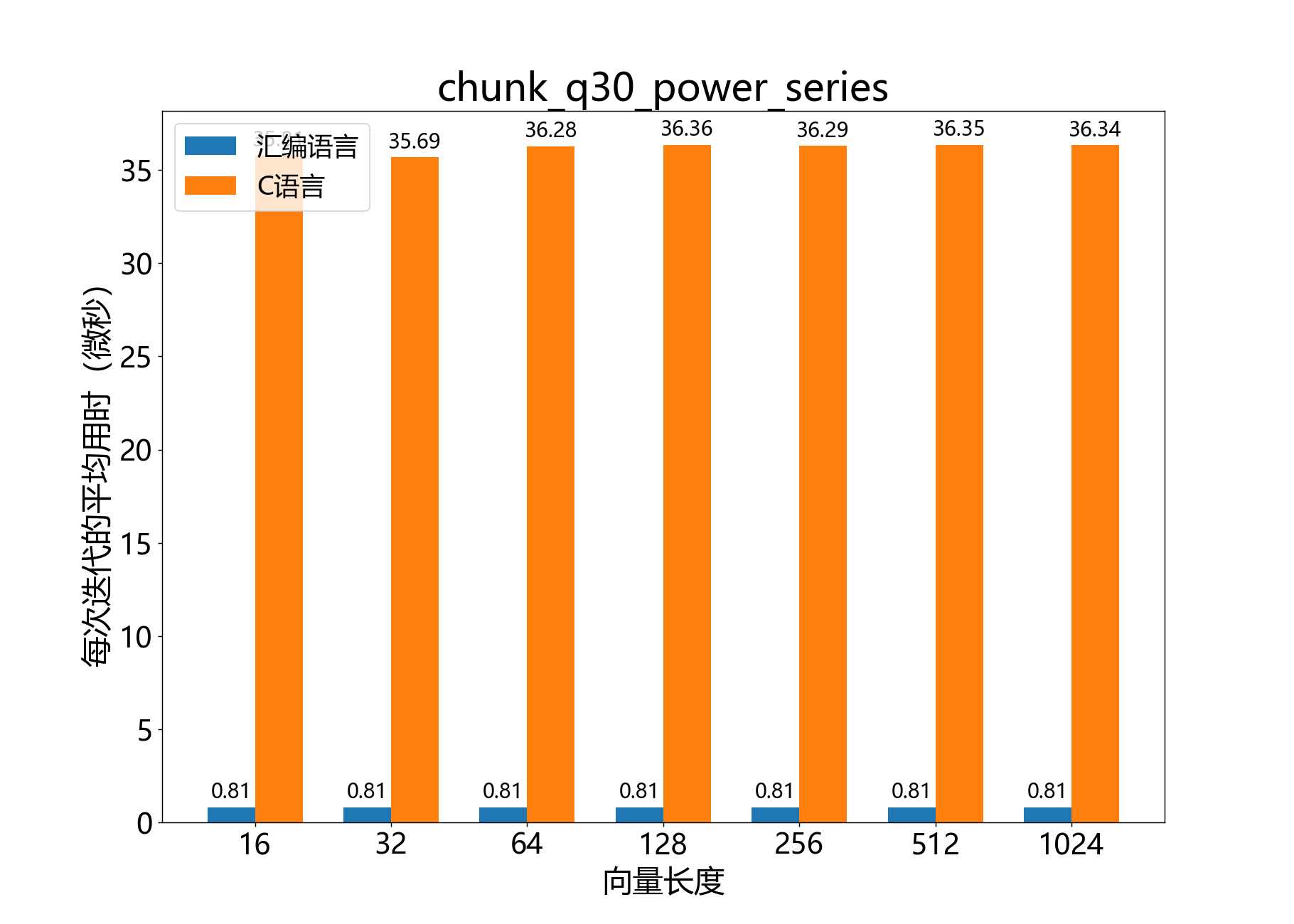
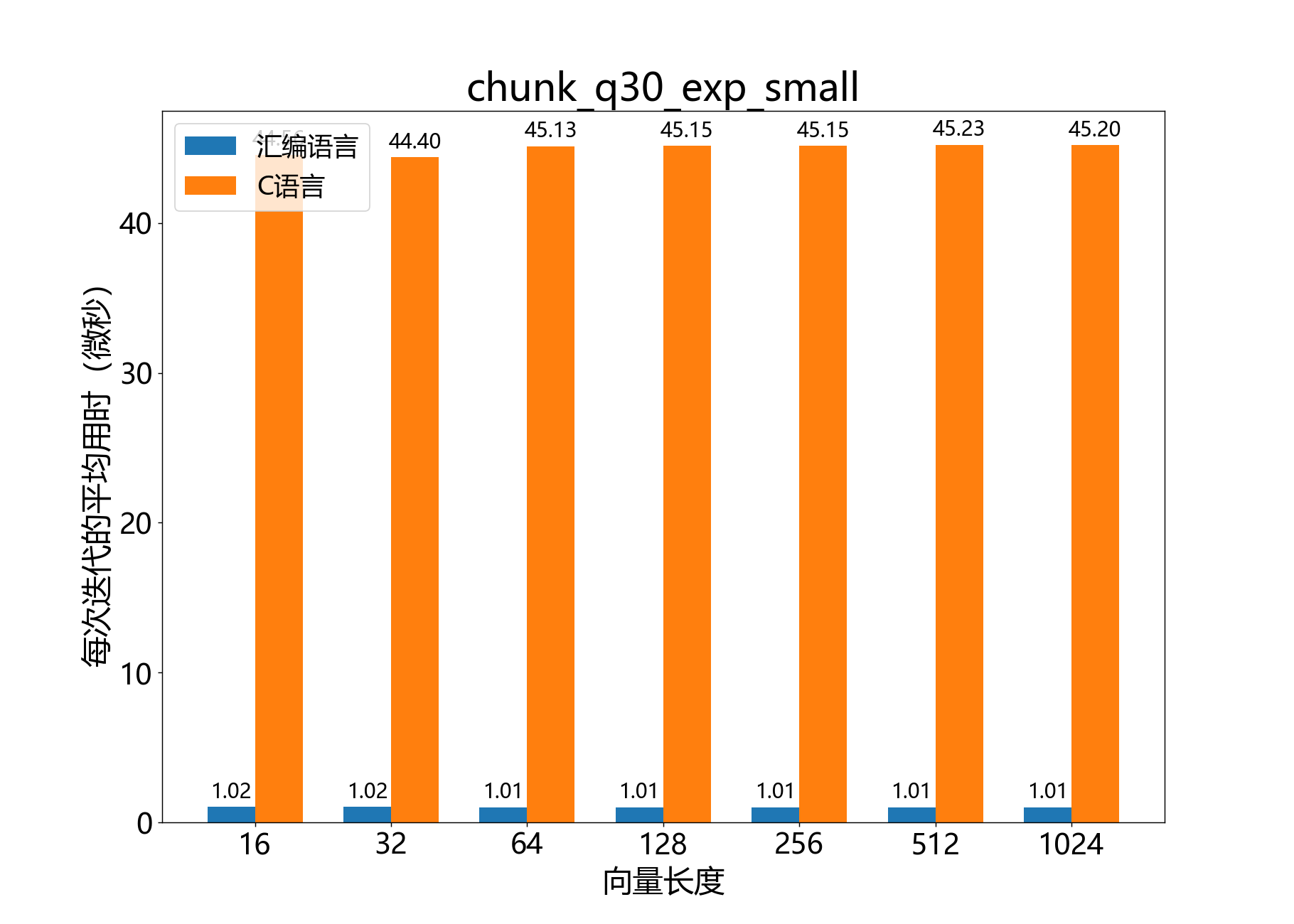
void chunk_q30_exp_small()
计算Q2.30值的向量块 bˉ 的 eb。
该函数计算向量块 bˉ 的每个元素的 ebk,其中 bˉ 是Q2.30值,接近0。结果使用 ex 在零附近的幂级数近似计算。建议仅在 −0.5≤bk⋅2−30≤0.5 时使用该函数。
输出向量块 aˉ 也以Q2.30格式表示。
操作:
ak←ebk⋅2−30for k∈{0..VPU_INT32_EPV}
参数:
q2_30 a[VPU_INT32_EPV] – [out] 输出向量块 aˉconst q2_30 b[VPU_INT32_EPV] – [in] 输入向量块 bˉ
参考性能: