Complex 16-bit Vector API
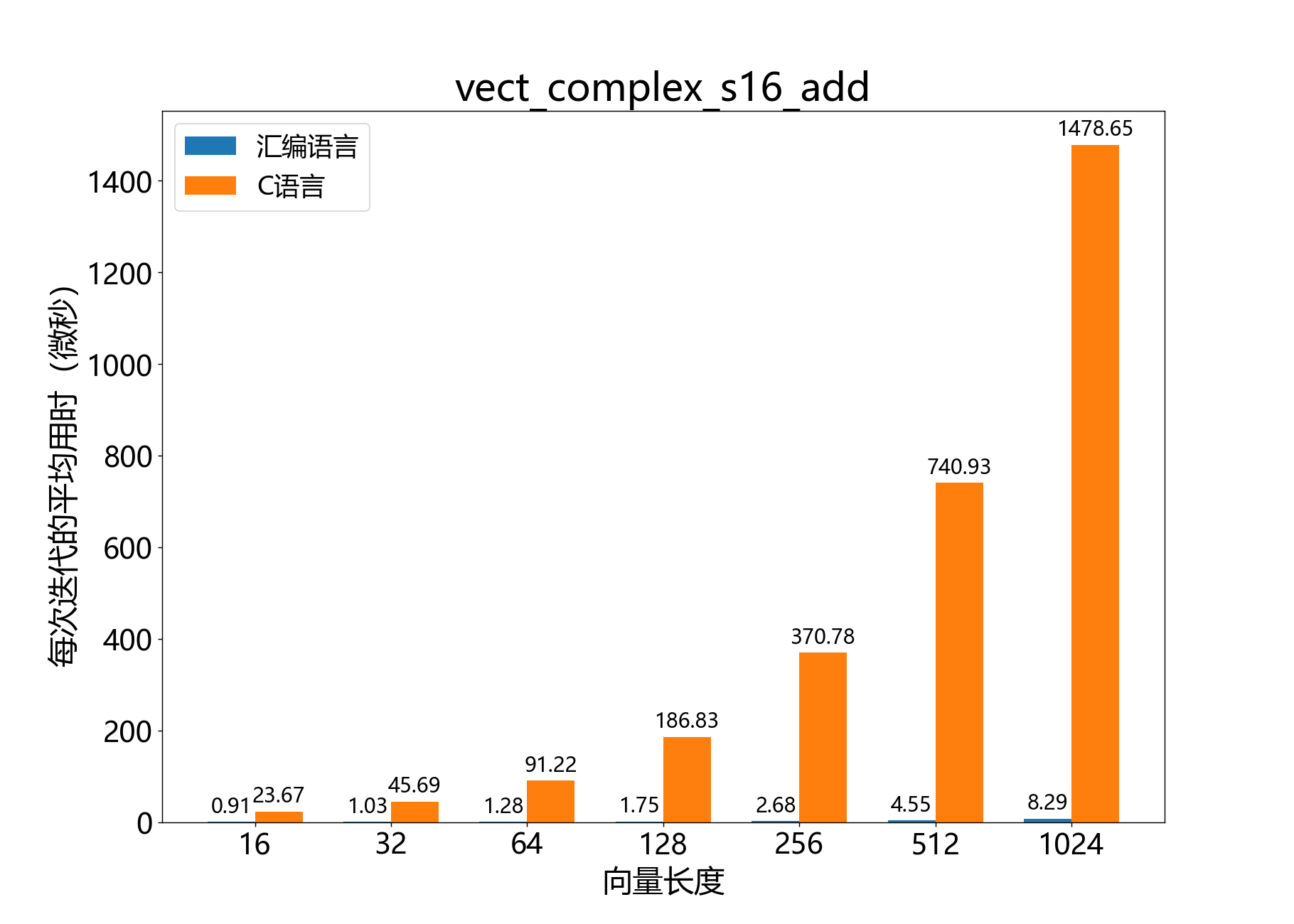
headroom_t vect_complex_s16_add()
将一个复合16位向量与另一个相加。
a_real[] 和 a_imag[] 共同表示复合16位输出尾数向量 aˉ。其中 Re{ak} 是 a_real[k],Im{ak} 是 a_imag[k]。
b_real[] 和 b_imag[] 共同表示复合16位输入尾数向量 bˉ。其中 Re{bk} 是 b_real[k],Im{bk} 是 b_imag[k]。
c_real[] 和 c_imag[] 共同表示复合16位输入尾数向量 cˉ。其中 Re{ck} 是 c_real[k],Im{ck} 是 c_imag[k]。
每个输入向量必须从字对齐的地址开始。该操作可以在输入 b_real[]、b_imag[]、c_real[] 和 c_imag[] 上安全地原地执行。
length 是每个向量中的元素数量。
b_shr 和 c_shr 是应用于 bˉ 和 cˉ 的有符号算术右移。
操作:
bk′←sat16(⌊bk⋅2−b_shr⌋)ck′←sat16(⌊ck⋅2−c_shr⌋)Re{ak}←Re{bk′}+Re{ck′}Im{ak}←Im{bk′}+Im{ck′} for k∈0 ... (length−1)
块浮点数:
如果 bˉ 和 cˉ 是BFP向量 bˉ⋅2b_exp 和 cˉ⋅2c_exp 的复合16位尾数,则结果向量 aˉ 是BFP向量 aˉ⋅2a_exp 的复合16位尾数。
在这种情况下,必须选择 bshr 和 cshr,使得 a_exp=b_exp+b_shr=c_exp+c_shr。只有当尾数与相同的指数关联时,才有意义地相加或相减。
函数 vect_complex_s16_add_prepare() 可以根据输入指数 b_exp 和 c_exp 以及输入头空间 b_hr 和 c_hr 来获取 a_exp、b_shr 和 c_shr 的值。
参数:
-
int16_t a_real[] – [out] 复合输出向量 aˉ 的实部
-
int16_t a_imag[] – [out] 复合输出向量 aˉ 的虚部
-
const int16_t b_real[] – [in] 复合输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复合输入向量 bˉ 的虚部
-
const int16_t c_real[] – [in] 复合输入向量 cˉ 的实部
-
const int16_t c_imag[] – [in] 复合输入向量 cˉ 的虚部
-
const unsigned length – [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量
-
const right_shift_t b_shr – [in] 应用于 bˉ 的右移量
-
const right_shift_t c_shr – [in] 应用于 cˉ 的右移量
返回值:
输出向量 aˉ 的头空间。
异常:
如果 a_real、a_imag、b_real、b_imag、c_real 或 c_imag 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐)。
另��请参阅:
vect_complex_s16_add_prepare()
参考性能:
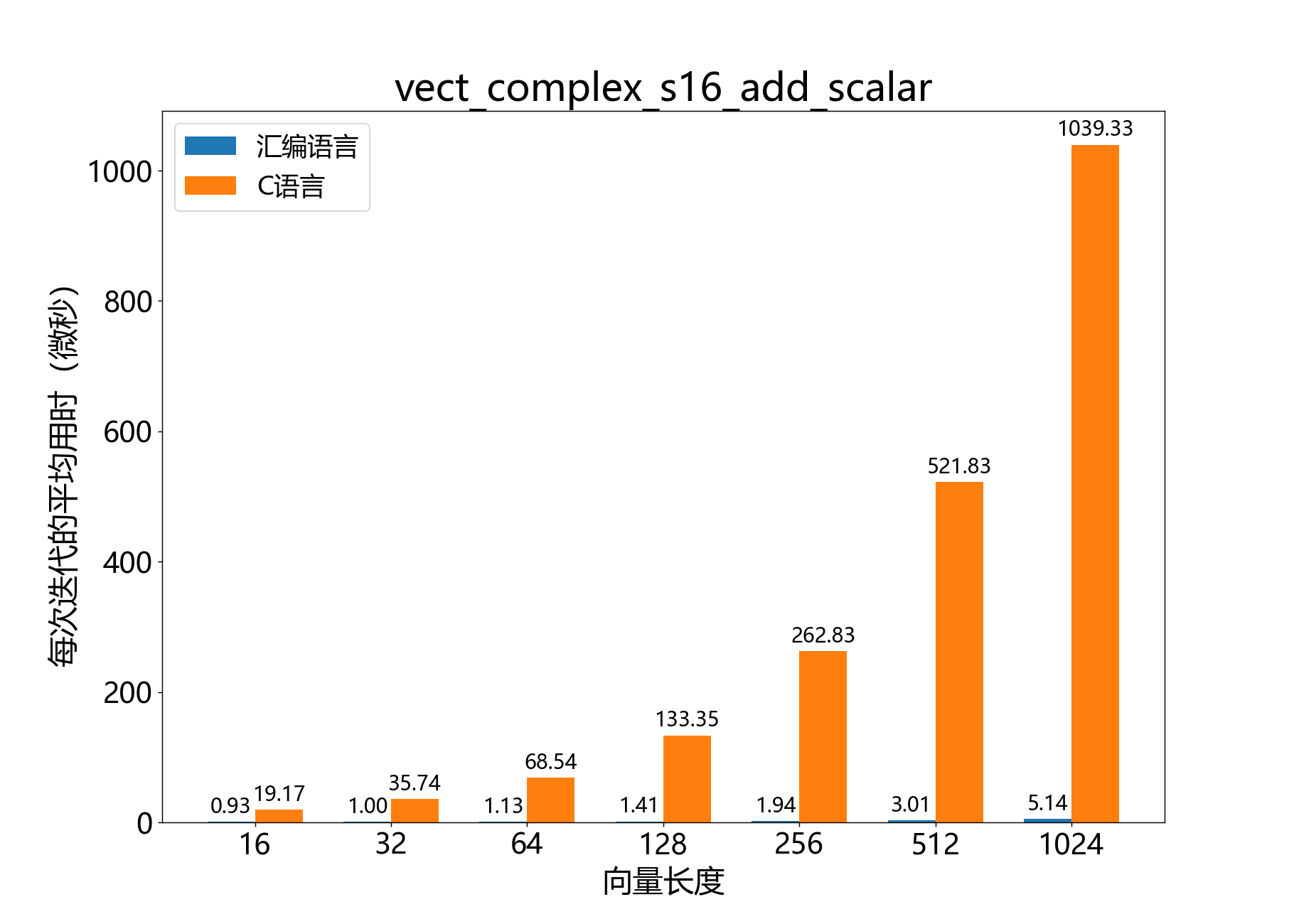
headroom_t vect_complex_s16_add_scalar()
将一个标量添加到复数16位向量中。
a[]和b[]分别表示复数16位尾数向量 aˉ 和 bˉ。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行。
c是要添加到 bˉ 的每个元素的复数标量 c。
length是每个向量中的元素数量。
b_shr是应用于 bˉ 的带符号算术右移位数。
该操作可以描述如下:
bk′←sat16(⌊bk⋅2−b_shr⌋)Re{ak}←Re{bk′}+Re{c}Im{ak}←Im{bk′}+Im{c} 其中 k∈0 ... (length−1)
块浮点数:
如果 bˉ 的元素是BFP向量 bˉ⋅2b_exp 的复数尾数,并且 c 是浮点数 c⋅2c_exp 的尾数,则结果向量 aˉ 是BFP向量 aˉ⋅2a_exp 的尾数。
在这种情况下,必须选择 b_shr 和 c_shr 使得 a_exp=b_exp+b_shr=c_exp+c_shr。只有当尾数与相同的指数相关联时,加法或减法才有意义。
函数 vect_complex_s16_add_scalar_prepare() 可以根据输入的指数 b_exp 和 c_exp 以及输入的头空间 b_hr 和 c_hr 来获取 a_exp、b_shr 和 c_shr 的值。
注意,c_shr 是 vect_complex_s16_add_scalar_prepare() 的输出,但它不是此函数的参数。由 vect_complex_s16_add_scalar_prepare() 产生的 c_shr 应由用户应用,并将结果作为输入 c 传递。
参数:
-
int16_t a_real[] – [out] 复数输出向量 aˉ 的实部
-
int16_t a_imag[] – [out] 复数输出向量 aˉ 的虚部
-
const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部
-
const complex_s16_t c – [in] 复数输入标量 c
-
const unsigned length – [in] 向量 aˉ 和 bˉ 中的元素数量
-
const right_shift_t b_shr – [in] 应用于 bˉ 的右移位数
返回值:
异常:
ET_LOAD_STORE 如果 a 或 b 不是字对齐的(参见 笔记:向量对齐)
参见:
vect_complex_s16_add_scalar_prepare()
参考性能:
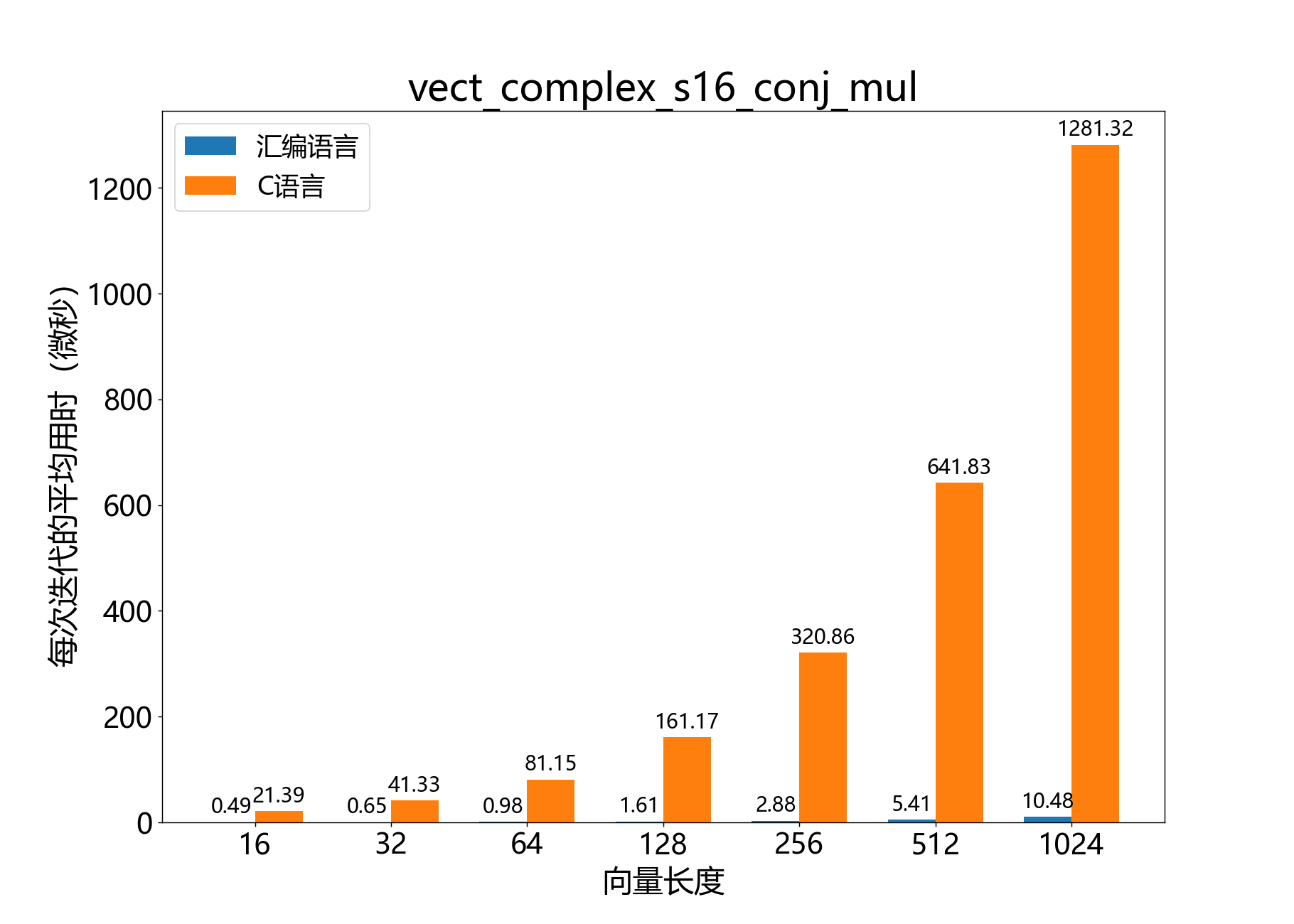
headroom_t vect_complex_s16_conj_mul()
逐元素将一个复数16位向量与另一个的共轭相乘。
a_real[] 和 a_imag[] 一起表示复数16位输出尾数向量 aˉ。每个 Re{ak} 是 a_real[k],每个 Im{ak} 是 a_imag[k]。
b_real[] 和 b_imag[] 一起表示复数16位输入尾数向量 bˉ。每个 Re{bk} 是 b_real[k],每个 Im{bk} 是 b_imag[k]。
c_real[] 和 c_imag[] 一起表示复数16位输入尾数向量 cˉ。每个 Re{ck} 是 c_real[k],每个 Im{ck} 是 c_imag[k]。
每个输入向量必须从字对齐的地址开始。该操作可以在输入 b_real[]、b_imag[]、c_real[] 和 c_imag[] 上安全地原地执行。
length 是向量中的元素数量。
a_shr 是应用于保存倒数第二个结果的32位累加器的无符号算术右移。
操作:
vk=←Re{bk}⋅Re{ck}+Im{bk}⋅Im{ck}sk=←Im{bk}⋅Re{ck}−Re{bk}⋅Im{ck}Re{ak}←round(sat16(vk��⋅2−a_shr))Im{ak}←round(sat16(sk⋅2−a_shr)) 其中 k∈0 ... (length−1)
参数:
int16_t a_real[] – [out] 复数输出向量 aˉ 的实部int16_t a_imag[] – [out] 复数输出向量 aˉ 的虚部const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部const int16_t c_real[] – [in] 复数输入向量 cˉ 的实部const int16_t c_imag[] – [in] 复数输入向量 cˉ 的虚部const unsigned length– [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量const right_shift_t a_shr – [in] 应用于32位中间结果的右移量
返回值:
异常:
- ET_LOAD_STORE 如果
a_real、a_imag、b_real、b_imag、c_real或c_imag不是字对齐的(参见笔记:向量对齐)
参见:
- vect_complex_s16_mul_prepare
参考性能:
headroom_t vect_complex_s16_headroom()
计算复数16位数组的头空间。
N位整数的头空间是整数值左移而不丢失任何信息的位数。等效地,它比领先的符号位少一位。
complex_s16_t 结构体的头空间是其16位字段 re 和 im 的头空间的最小值。
complex_s16_t 数组的头空间是其每个 complex_s16_t 元素的头空间的最小值。
该函数高效地遍历 xˉ 的元素以确定其头空间。
b_real[] 和 b_imag[] 一起表示复数16位输入尾数向量 bˉ。
length 是 b_real[] 和 b_imag[] 中的元素数量。
操作:
min{HR16(x0),HR16(x1),...,HR16(xlength−1)}
参数:
const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部const unsigned length– [in] 向量 xˉ 中的元素数量
返回值:
参见:
- vect_s16_headroom
- vect_s32_headroom
- vect_complex_s32_headroom
参考性能:
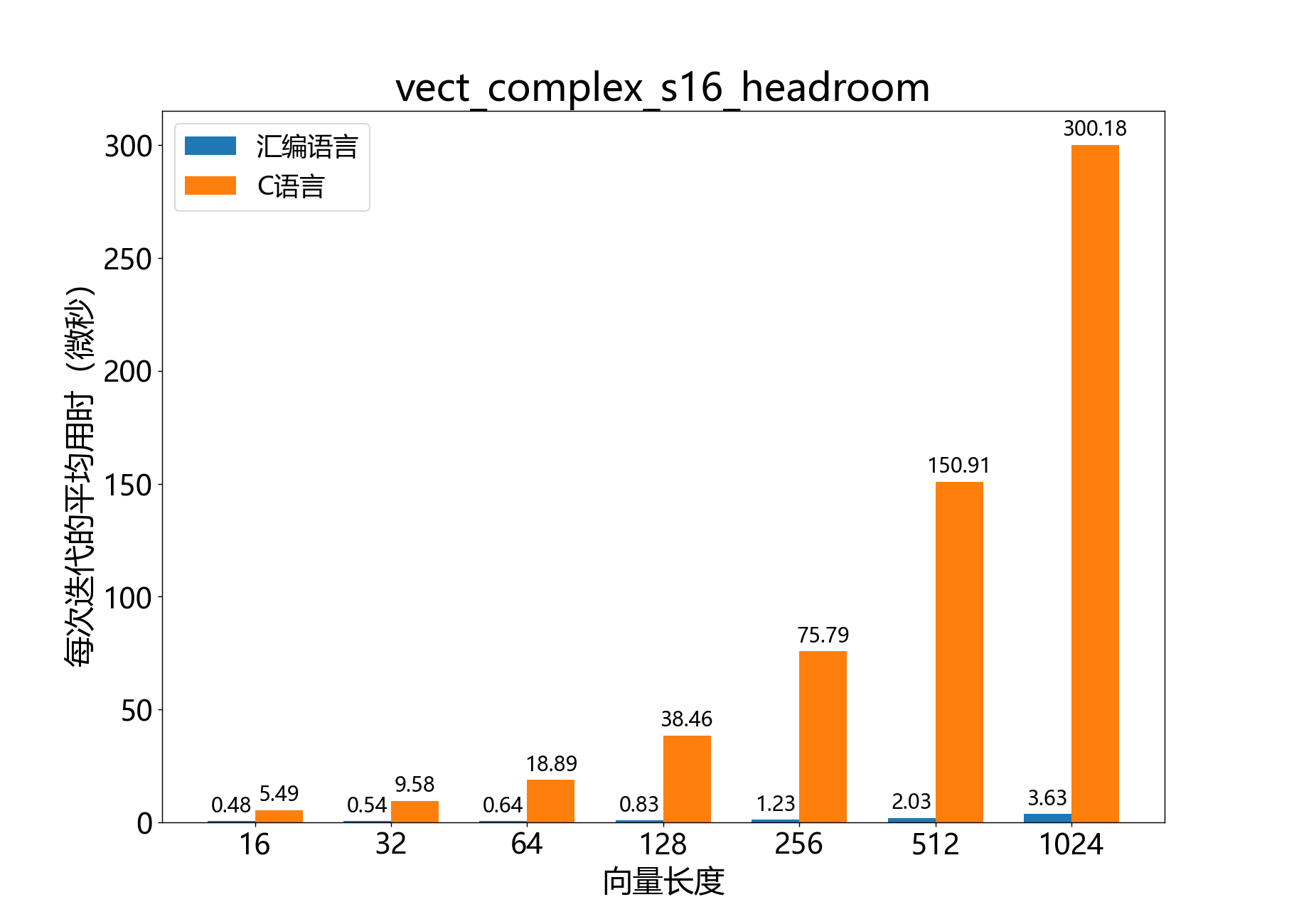
headroom_t vect_complex_s16_mag()
计算复合16位向量每个元素的幅值。
a[] 表示实部的16位输出尾数向量 aˉ。
b_real[] 和 b_imag[] 一起表示复合16位输入尾数向量 bˉ。每个 Re{bk} 是 b_real[k],每个 Im{bk} 是 b_imag[k]。
每个输入向量必须从字对齐的地址开始。此操作可以安全地原地执行在输入 b_real[] 或 b_imag[] 上。
length 是向量中的元素数量。
b_shr 是应用于 bˉ 元素的有符号算术右移。
rot_table 必须指向预先计算的用于计算幅值的复合向量表。table_rows 是表中的行数。
此函数执行的操作如下:
vkak其中 k←bk⋅2−b_shr←(Re{vk})2+(Im{vk})2∈0…(length−1)
参数:
-
int16_t a[] – [out] 实部输出向量 aˉ
-
const int16_t b_real[] – [in] 复合输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复合输入向量 bˉ 的虚部
-
const unsigned length – [in] 向量 aˉ 和 bˉ 中的元素数量
-
const right_shift_t b_shr – [in] 应用于 bˉ 的右移量
-
const int16_t* rot_table – [in] 计算幅值所需的预先计算的旋转表
-
const unsigned table_rows – [in] rot_table 中的行数
返回值:
headroom_t - 输出向量 aˉ 的头空间。
参考性能:
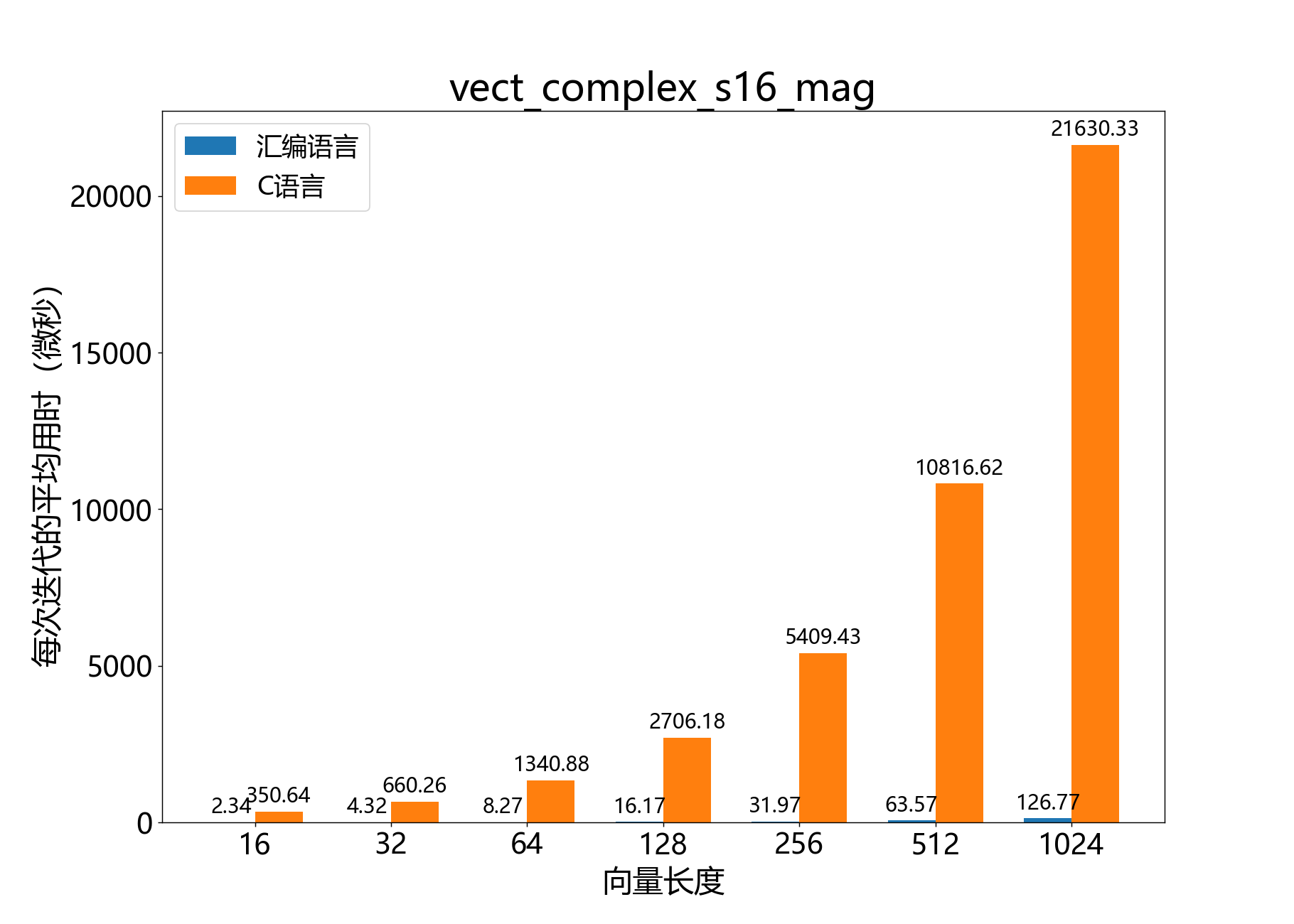
headroom_t vect_complex_s16_macc()
逐元素将一个复合16位向量与另一个向量相乘,并将结果累加到累加器中。
acc_real[] 和 acc_imag[] 一起表示复合16位累加器尾数向量 aˉ。每个 Re{ak} 是 acc_real[k],每个 Im{ak} 是 acc_imag[k]。
b_real[] 和 b_imag[] 一起表示复合16位输入尾数向量 bˉ。每个 Re{bk} 是 b_real[k],每个 Im{bk} 是 b_imag[k]。
c_real[] 和 c_imag[] 一起表示复合16位输入尾数向量 cˉ。每个 Re{ck} 是 c_real[k],每个 Im{ck} 是 c_imag[k]。
每个输入向量必须从字对齐的地址开始。
length 是向量中的元素数量。
acc_shr 是应用于累加器元素 ak 的有符号算术右移。
bc_sat 是应用于 bk 和 ck 的乘积后添加到累加器的无符号算术右移。
此函数执行的操作如下:
vk←Re{bk}⋅Re{ck}−Im{bk}⋅Im{ck}sk←Im{bk}⋅Re{ck}+Re{bk}⋅Im{ck}a^k←sat16(ak⋅2−acc_shr)Re{ak}←sat16(Re{a^k}+round(sat16(vk⋅2−bc_sat)))Im{ak}←sat16(Im{a^k}+round(sat16(sk⋅2−bc_sat))) 其中 k∈0 ... (length−1)
参数:
-
int16_t acc_real[] – [inout] 复合累加器 aˉ 的实部
-
int16_t acc_imag[] – [inout] 复合累加器 aˉ 的虚部
-
const int16_t b_real[] – [in] 复合输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复合输入向量 bˉ 的虚部
-
const int16_t c_real[] – [in] 复合输入向量 cˉ 的实部
-
const int16_t c_imag[] – [in] 复合输入向量 cˉ 的虚部
-
const unsigned length – [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量
-
const right_shift_t acc_shr – [in] 应用于累加器元素的有符号算术右移
-
const right_shift_t bc_sat – [in] 应用于元素 bk 和 ck 乘积的无符号算术右移
返回值:
headroom_t - 输出向量 aˉ 的头空间。
参考性能:
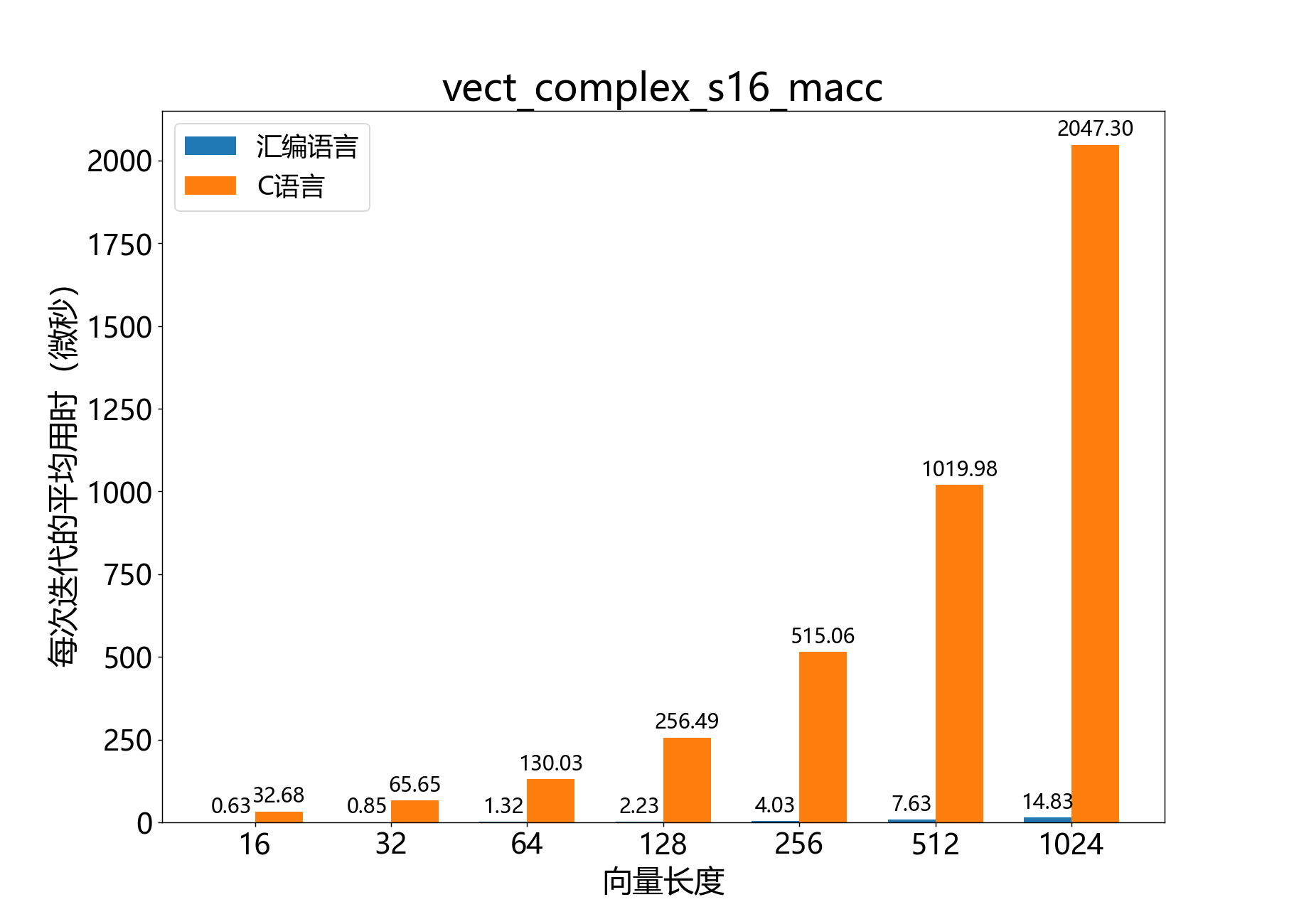
headroom_t vect_complex_s16_nmacc()
逐元素将一个复数16位向量与另一个相乘,并从累加器中减去结果。
acc_real[]和acc_imag[]一起表示复数16位累加器的尾数向量 aˉ。其中 Re{ak} 是 acc_real[k],Im{ak} 是 acc_imag[k]。
b_real[]和b_imag[]一起表示复数16位输入的尾数向量 bˉ。其中 Re{bk} 是 b_real[k],Im{bk} 是 b_imag[k]。
c_real[]和c_imag[]一起表示复数16位输入的尾数向量 cˉ。其中 Re{ck} 是 c_real[k],Im{ck} 是 c_imag[k]。
输入向量的每个元素必须从字对齐的地址开始。
length是每个向量中的元素数量。
acc_shr是应用于累加器 ak 的有符号算术右移。
bc_sat是应用于 bk 和 ck 的乘积后从累加器中减去之前的无符号算术右移。
操作:
vk←Re{bk}⋅Re{ck}−Im{bk}⋅Im{ck}sk←Im{bk}⋅Re{ck}+Re{bk}⋅Im{ck}a^k←sat16(ak⋅2−acc_shr)Re{ak}←sat16(Re{a^k}−round(sat16(vk⋅2−bc_sat)))Im{ak}←sat16(Im{a^k}−round(sat16(sk⋅2−bc_sat))) 其中 k∈0 ... (length−1)
块浮点数:
如果输入 bˉ 和 cˉ 是BFP向量 bˉ⋅2b_exp 和 cˉ⋅2c_exp 的尾数,并且输入 aˉ 是累加器BFP向量 aˉ⋅2a_exp,则输出的 aˉ 的值具有指数 2a_exp+acc_shr。
为了使累加在数学上有意义,必须选择 bc_sat 使得 a_exp+acc_shr=b_exp+c_exp+bc_sat。
函数 vect_complex_s16_nmacc_prepare() 可以根据输入的指数 a_exp、b_exp 和 c_exp 以及输入的头空间 a_hr、b_hr 和 c_hr 来获取 a_exp、acc_shr 和 bc_sat 的值。
参数:
-
int16_t acc_real[] – [inout] 复数累加器 aˉ 的实部
-
int16_t acc_imag[] – [inout] 复数累加器 aˉ 的虚部
-
const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部
-
const int16_t c_real[] – [in] 复数输入向量 cˉ 的实部
-
const int16_t c_imag[] – [in] 复数输入向量 cˉ 的虚部
-
const unsigned length – [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量
-
const right_shift_t acc_shr – [in] 应用于累加器元素的有符号算术右移
-
const right_shift_t bc_sat – [in] 应用于元素 bk 和 ck 乘积后从累加器中减去的无符号算术右移
返回值:
异常:
- 如果
acc_real、acc_imag、b_real、b_imag、c_real或c_imag不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐)
另请参阅:
vect_complex_s16_nmacc_prepare
参考性能:
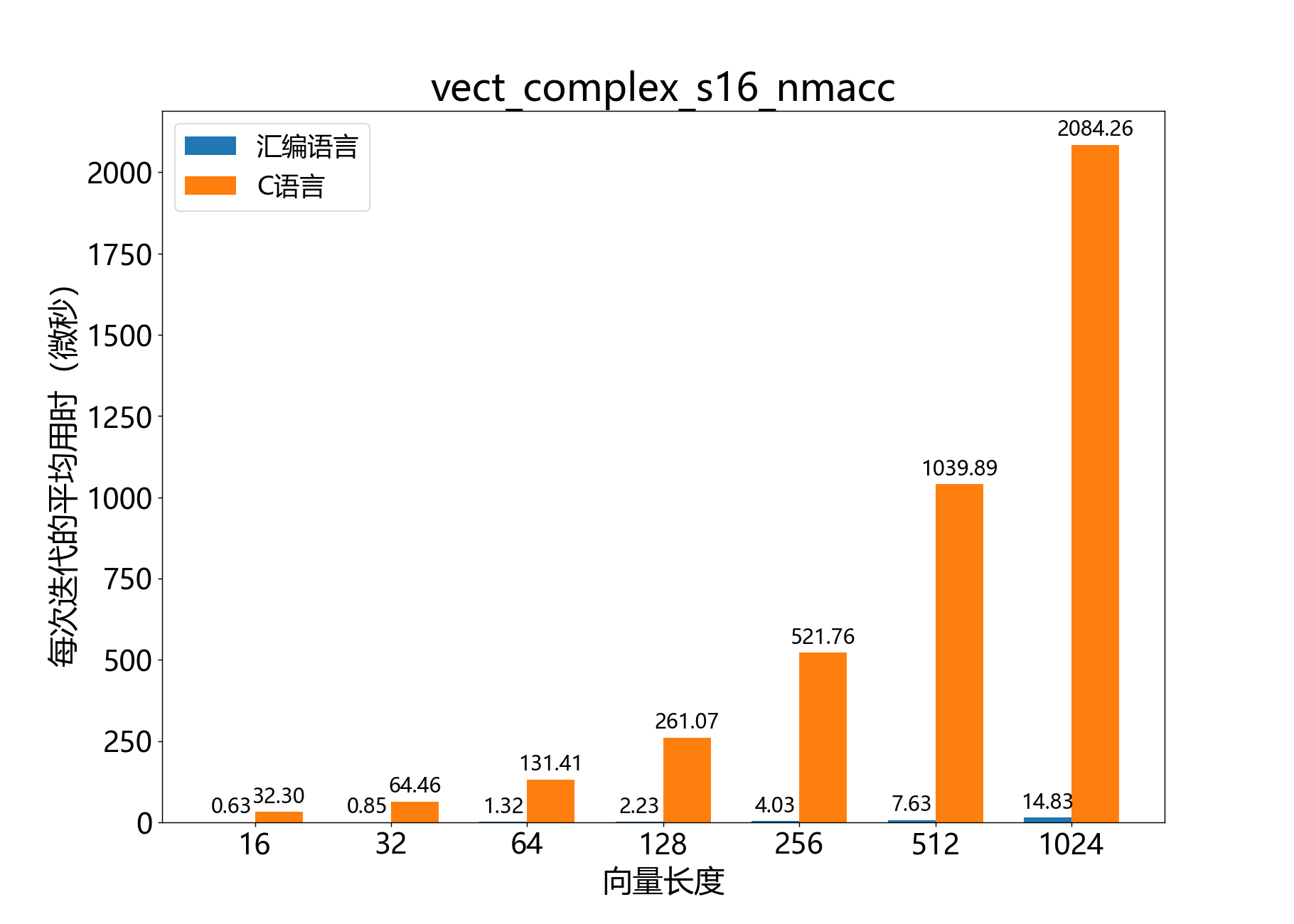
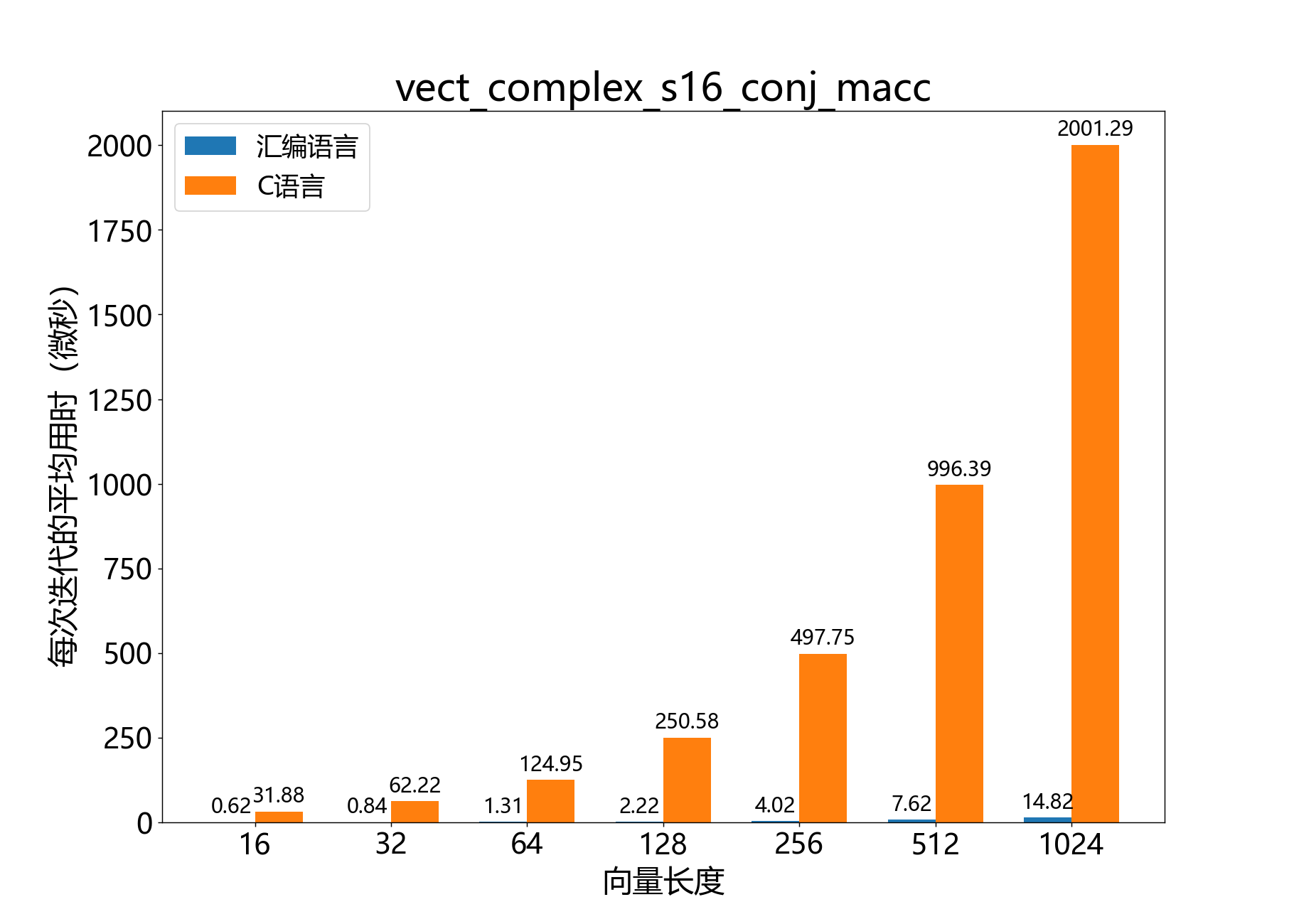
headroom_t vect_complex_s16_conj_macc()
逐元素将一个复数16位向量与另一个复数的共轭相乘,并将结果加到累加器中。
acc_real[]和acc_imag[]共同表示复数16位累加器尾数向量 aˉ。每个 Re{ak} 是 acc_real[k],每个 Im{ak} 是 acc_imag[k]。
b_real[]和b_imag[]共同表示复数16位输入尾数向量 bˉ。每个 Re{bk} 是 b_real[k],每个 Im{bk} 是 b_imag[k]。
c_real[]和c_imag[]共同表示复数16位输入尾数向量 cˉ。每个 Re{ck} 是 c_real[k],每个 Im{ck} 是 c_imag[k]。
每个输入向量必须从字对齐的地址开始。
length 是向量中的元素数量。
acc_shr 是应用于累加器 ak 的有符号算术右移。
bc_sat 是应用于 bk 和 ck∗ 的乘积后加到累加器中的无符号算术右移。
操作:
vk←Re{bk}⋅Re{ck}+Im{bk}⋅Im{ck}sk←Im{bk}⋅Re{ck}−Re{bk}��⋅Im{ck}a^k←sat16(ak⋅2−acc_shr)Re{ak}←sat16(Re{a^k}+round(sat16(vk⋅2−bc_sat)))Im{ak}←sat16(Im{a^k}+round(sat16(sk⋅2−bc_sat))) 其中 k∈0 ... (length−1)
块浮点数:
如果输入 bˉ 和 cˉ 是BFP向量 bˉ⋅2b_exp 和 cˉ⋅2c_exp 的尾数,并且输入 aˉ 是累加器BFP向量 aˉ⋅2a_exp,那么 aˉ 的输出值具有指数 2a_exp+acc_shr。
为了使累加在数学上有意义,必须选择 bc_sat ,使得 a_exp+acc_shr=b_exp+c_exp+bc_sat。
可以使用函数 vect_complex_s16_macc_prepare() 根据输入指数 a_exp、b_exp 和 c_exp 以及输入头空间 a_hr、b_hr 和 c_hr 来获取 a_exp、acc_shr 和 bc_sat 的值。
参数:
int16_t acc_real[] – [inout] 复数累加器 aˉ 的实部int16_t acc_imag[] – [inout] 复数累加器 aˉ 的虚部const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部const int16_t c_real[] – [in] 复数输入向量 cˉ 的实部const int16_t c_imag[] – [in] 复数输入向量 cˉ 的虚部const unsigned length – [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量const right_shift_t acc_shr – [in] 应用于累加器元素的有符号算术右移const right_shift_t bc_sat – [in] 应用于元素 bk 和 ck∗ 的乘积后加到累加器中的无符号算术右移
返回值:
异常:
- ET_LOAD_STORE 如果
acc_real、acc_imag、b_real、b_imag、c_real 或 c_imag 不是字对齐的(参见 笔记:向量对齐)
参见:
vect_complex_s16_conj_macc_prepare
参考性能:
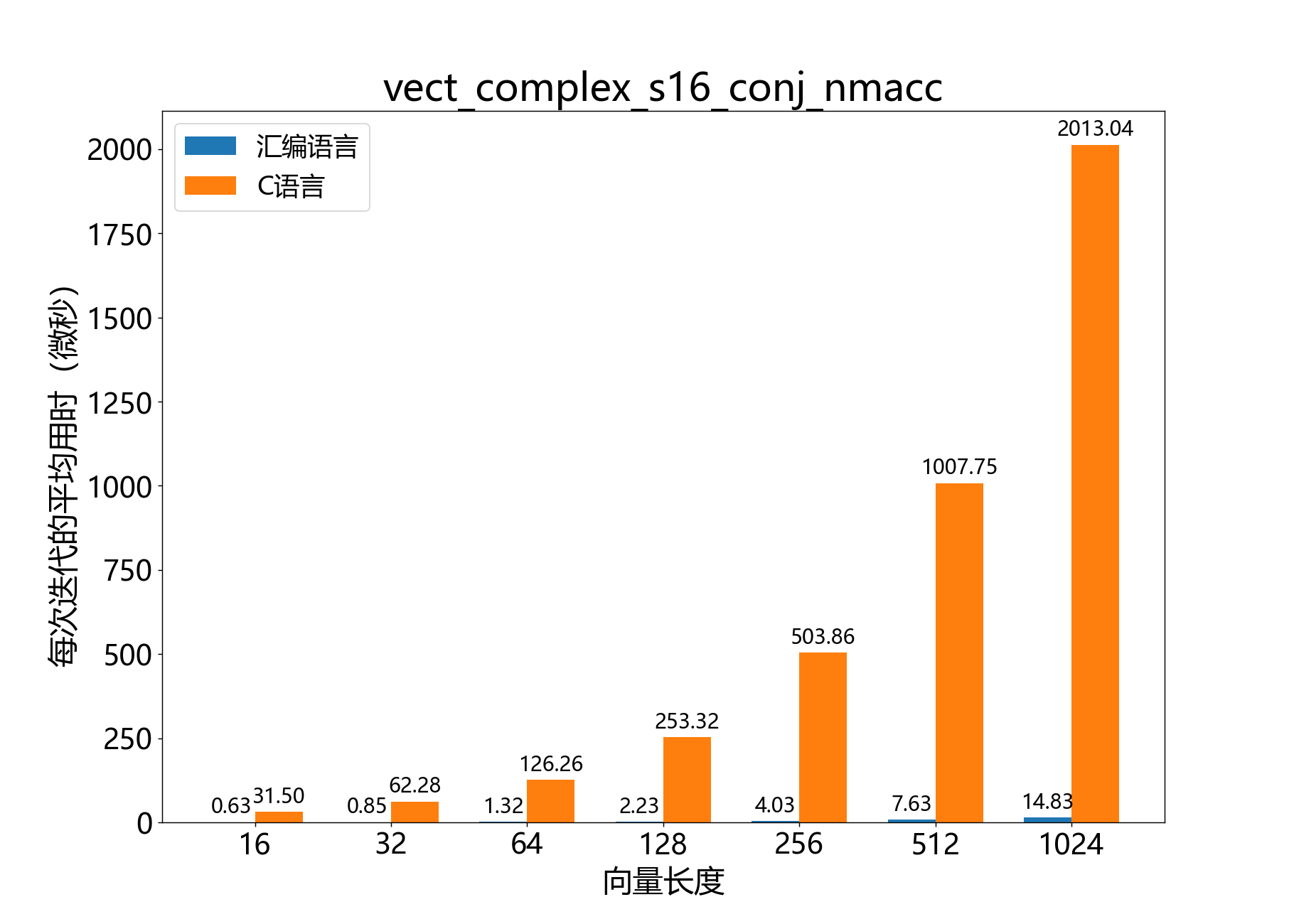
headroom_t vect_complex_s16_conj_nmacc()
逐元素将一个复数16位向量乘以另一个复数的共轭,并从累加器中减去结果。
acc_real[] 和 acc_imag[] 分别表示复数16位累加器的实部向量 aˉ。每个 Re{ak} 对应 acc_real[k],每个 Im{ak} 对应 acc_imag[k]。
b_real[] 和 b_imag[] 分别表示复数16位输入的实部向量 bˉ。每个 Re{bk} 对应 b_real[k],每个 Im{bk} 对应 b_imag[k]。
c_real[] 和 c_imag[] 分别表示复数16位输入的实部向量 cˉ。每个 Re{ck} 对应 c_real[k],每个 Im{ck} 对应 c_imag[k]。
输入向量的每个元素必须从字对齐的地址开始。
length 是向量中的元素数量。
acc_shr 是应用于累加器 ak 的有符号算术右移量。
bc_sat 是应用于 bk 和 ck∗ 的乘积后从累加器中减去之前的无符号算术右移量。
操作:
vk←Re{bk}⋅Re{ck}+Im{bk}⋅Im{ck}sk←Im{bk}⋅Re{ck}−Re{bk}⋅Im{ck}a^k←sat16(ak⋅2−acc_shr)Re{ak}←sat16(Re{a^k}−round(sat16(vk⋅2−bc_sat)))Im{ak}←sat16(Im{a^k}−round(sat16(sk⋅2−bc_sat))) 其中 k∈0 ... (length−1)
块浮点数:
如果输入 bˉ 和 cˉ 是 BFP 向量 bˉ⋅2b_exp 和 cˉ⋅2c_exp 的尾数,并且输入 aˉ 是累加器 BFP 向量 aˉ⋅2a_exp,则输出向量 aˉ 的指数为 2a_exp+acc_shr。
为了使数学上的累加有意义,必须选择 bc_sat,使得 a_exp+acc_shr=b_exp+c_exp+bc_sat。
函数 vect_complex_s16_macc_prepare() 可以根据输入的指数 a_exp、b_exp 和 c_exp 以及输入的头空间 a_hr、b_hr 和 c_hr 来获取 a_exp、acc_shr 和 bc_sat 的值。
参数:
int16_t acc_real[] – [inout] 复数累加器的实部 aˉint16_t acc_imag[] – [inout] 复数累加器的虚部 aˉconst int16_t b_real[] – [in] 复数输入向量的实部 bˉconst int16_t b_imag[] – [in] 复数输入向量的虚部 bˉconst int16_t c_real[] – [in] 复数输入向量的实部 cˉconst int16_t c_imag[] – [in] 复数输入向量的虚部 cˉconst unsigned length – [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量const right_shift_t acc_shr – [in] 应用于累加器元素的有符号算术右移量const right_shift_t bc_sat – [in] 应用于 bk 和 ck∗ 的乘积从累加器中减去之前的无符号算术右移量
返回值: 输出向量 aˉ 的头空间。
异常: 如果 acc_real、acc_imag、b_real、b_imag、c_real 或 c_imag 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐)
参考性能:
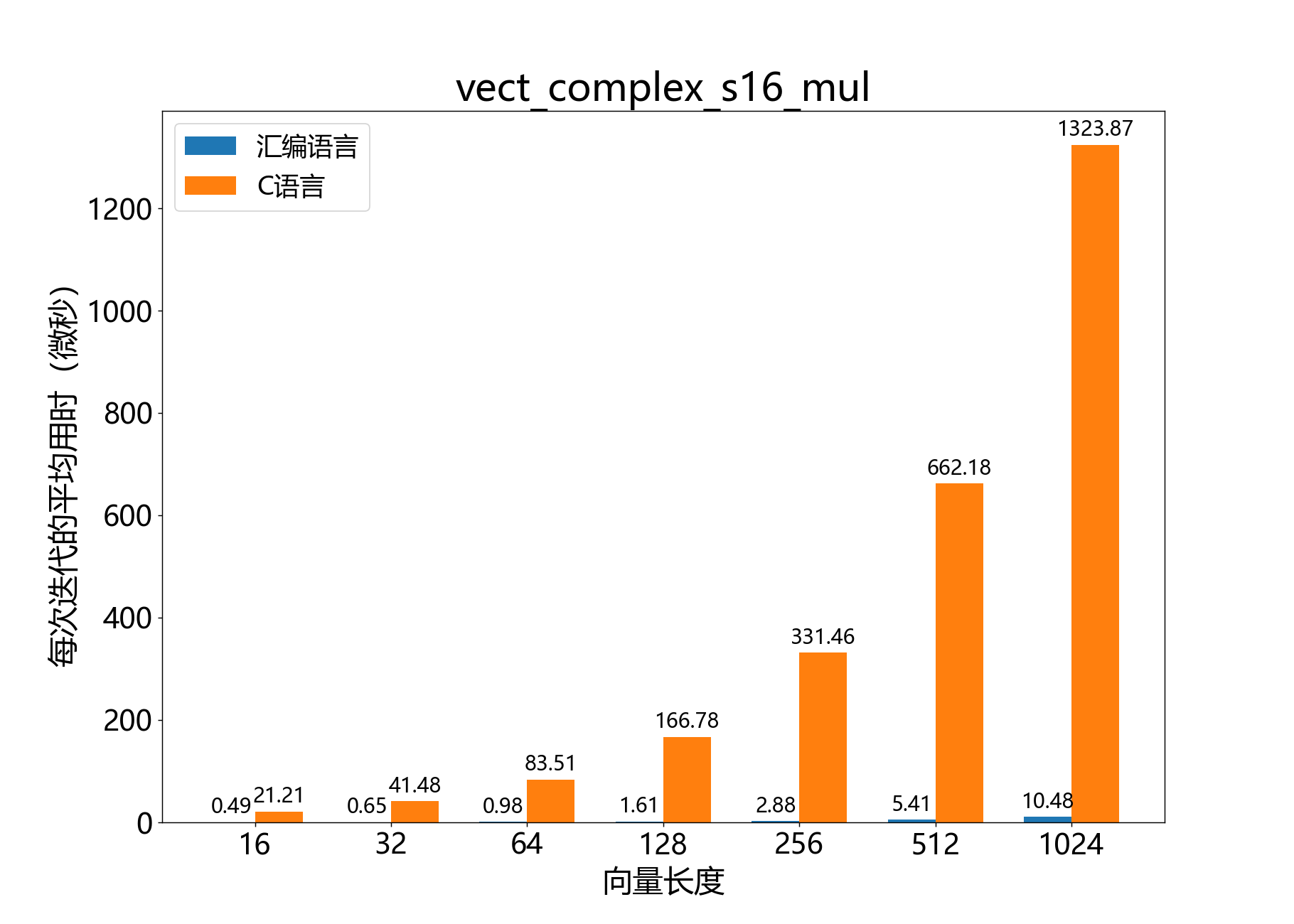
headroom_t vect_complex_s16_mul()
逐元素将一个复数16位向量乘以另一个复数16位向量。
a_real[] 和 a_imag[] 分别表示复数16位输出的实部向量 aˉ。每个 Re{ak} 对应 a_real[k],每个 Im{ak} 对应 a_imag[k]。
b_real[] 和 b_imag[] 分别表示复数16位输入的实部向量 bˉ。每个 Re{bk} 对应 b_real[k],每个 Im{bk} 对应 b_imag[k]。
c_real[] 和 c_imag[] 分别表示复数16位输入的实部向量 cˉ。每个 Re{ck} 对应 c_real[k],每个 Im{ck} 对应 c_imag[k]。
输入向量的每个元素必须从字对齐的地址开始。该操作可以在输入的 b_real[]、b_imag[]、c_real[] 和 c_imag[] 上安全地原地执行。
length 是向量中的元素数量。
a_shr 是应用于保存中间结果的32位累加器的无符号算术右移量。
操作:
vk=←Re{bk}⋅Re{ck}−Im{bk}⋅Im{ck}sk=←Im{bk}⋅Re{ck}+Re{bk}⋅Im{ck}Re{ak}←round(sat16(vk⋅2−a_shr))Im{ak}←round(sat16(sk⋅2−a_shr)) 其中 k∈0 ... (length−1)
块浮点数:
如果 bˉ 是复数16位向量 bˉ⋅2b_exp 的尾数,cˉ 是复数16位向量 cˉ⋅2c_exp 的尾数,aˉ 是复数16位向量 aˉ⋅2a_exp 的尾数,则输出向量 aˉ 的指数为 2a_exp+a_shr。
函数 vect_complex_s16_mul_prepare() 可以根据输入的指数 b_exp 和 c_exp 以及输入的头空间 b_hr 和 c_hr 来获取 a_exp 和 a_shr 的值。
参数:
int16_t a_real[] – [out] 复数输出向量的实部 aˉint16_t a_imag[] – [out] 复数输出向量的虚部 aˉconst int16_t b_real[] – [in] 复数输入向量的实部 bˉconst int16_t b_imag[] – [in] 复数输入向量的虚部 bˉconst int16_t c_real[] – [in] 复数输入向量的实部 cˉconst int16_t c_imag[] – [in] 复数输入向量的虚部 cˉconst unsigned length – [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量const right_shift_t a_shr – [in] 应用于保存中间结果的32位累加器的右移量
返回值:
异常:
- 如果
a_real、a_imag、b_real、b_imag、c_real 或 c_imag 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐)
参见:
vect_complex_s16_mul_prepare
参考性能:
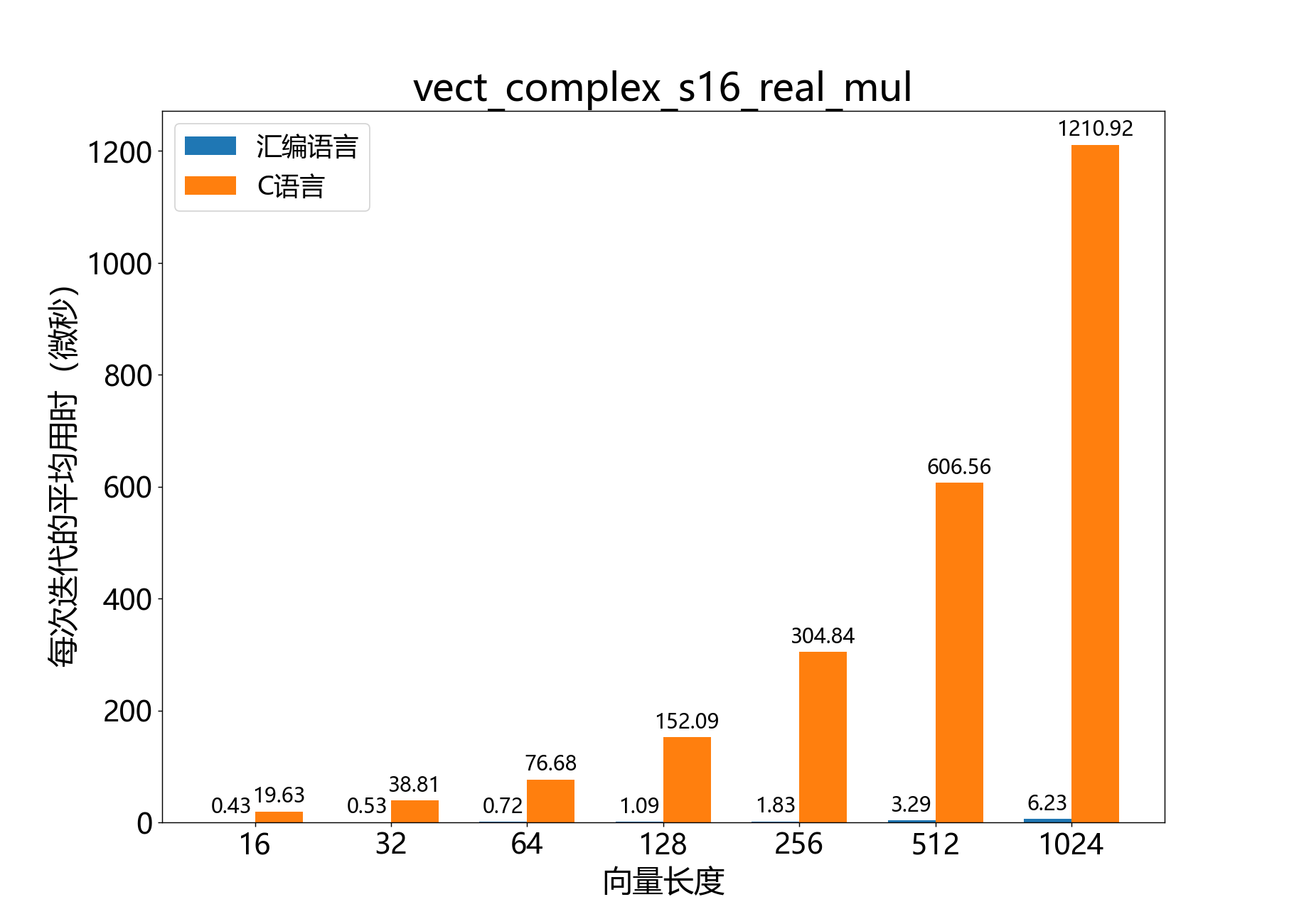
headroom_t vect_complex_s16_real_mul()
逐元素将复数16位向量与实数16位向量相乘。
a_real[] 和 a_imag[] 共同表示复数16位输出尾数向量 aˉ。其中 Re{ak} 对应 a_real[k],Im{ak} 对应 a_imag[k]。
b_real[] 和 b_imag[] 共同表示复数16位输入尾数向量 bˉ。其中 Re{bk} 对应 b_real[k],Im{bk} 对应 b_imag[k]。
c_real[] 表示实数16位输入尾数向量 cˉ。
每个输入向量必须从字对齐的地址开始。这个操作可以在 b_real[]、b_imag[] 和 c_real[] 上安全地原地执行。
length 是向量中的元素数量。
a_shr 是应用于保存倒数第二个结果的32位累加器的无符号算术右移。
该操作由以下方程描述:
vkskRe{ak}Im{ak}=Re{bk}⋅ck=Im{bk}⋅ck=round(sat16(vk⋅2−a_shr))=round(sat16(sk⋅2−a_shr))
其中 k 的取值范围为 0 ... (length−1)。
如果 bˉ 是复数16位BFP向量 bˉ⋅2b_exp 的尾数,并且 cˉ 是浮点值 c⋅2c_exp 的复数16位尾数,则结果向量 aˉ 是BFP向量 aˉ⋅2a_exp 的尾数,其中 a_exp=b_exp+c_exp+a_shr。
函数 vect_s16_real_mul_prepare() 可以根据输入的指数 b_exp 和 c_exp 以及输入的头空间 b_hr 和 c_hr 来获取 a_exp 和 a_shr 的值。
参数:
-
int16_t a_real[] – [out] 复数输出向量 aˉ 的实部
-
int16_t a_imag[] – [out] 复数输出向量 aˉ 的虚部
-
const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部
-
const int16_t c_real[] – [in] 实数输入向量 cˉ
-
const unsigned length – [in] 向量 aˉ、bˉ 和 cˉ 中的元素数量
-
const right_shift_t a_shr – [in] 应用于32位中间结果的右移量
返回值:
异常:
- 如果
a_real、a_imag、b_real、b_imag 或 c_real 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐)
参考性能:
headroom_t vect_complex_s16_real_scale()
将复�数16位向量乘以实数标量。
a_real[] 和 a_imag[] 共同表示复数16位输出尾数向量 aˉ。其中 Re{ak} 对应 a_real[k],Im{ak} 对应 a_imag[k]。
b_real[] 和 b_imag[] 共同表示复数16位输入尾数向量 bˉ。其中 Re{bk} 对应 b_real[k],Im{bk} 对应 b_imag[k]。
每个输入向量必须从字对齐的地址开始。这个操作可以在 b_real[] 和 b_imag[] 上安全地原地执行。
c 是实数16位输入尾数 c。
length 是向量中的元素数量。
a_shr 是应用于保存倒数第二个结果的32位累加器的无符号算术右移。
该操作由以下方程描述:
vkskRe{ak}Im{ak}=Re{bk}⋅c=Im{bk}⋅c=round(sat16(vk⋅2−a_shr))=round(sat16(sk⋅2−a_shr))
其中 k 的取值范围为 0 ... (length−1)。
如果 bˉ 是复数16位BFP向量 bˉ⋅2b_exp 的尾数,并且 c 是浮点值 c⋅2c_exp 的复数16位尾数,则结果向量 aˉ 是BFP向量 aˉ⋅2a_exp 的尾数,其中 a_exp=b_exp+c_exp+a_shr。
函数 vect_complex_s16_real_scale_prepare() 可以根据输入的指数 b_exp 和 c_exp 以及输入的头空间 b_hr 和 c_hr 来获取 a_exp 和 a_shr 的值。
参数:
-
int16_t a_real[] – [out] 复数输出向量 aˉ 的实部
-
int16_t a_imag[] – [out] 复数输出向量 aˉ 的虚部
-
const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部
-
const int16_t c – [in] 实数输入尾数 c
-
const unsigned length – [in] 向量 aˉ 和 bˉ 中的元素数量
-
const right_shift_t a_shr – [in] 应用于32位中�间结果的右移量
返回值:
异常:
- 如果
a_real、a_imag、b_real、b_imag 或 c 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐)
参考性能:
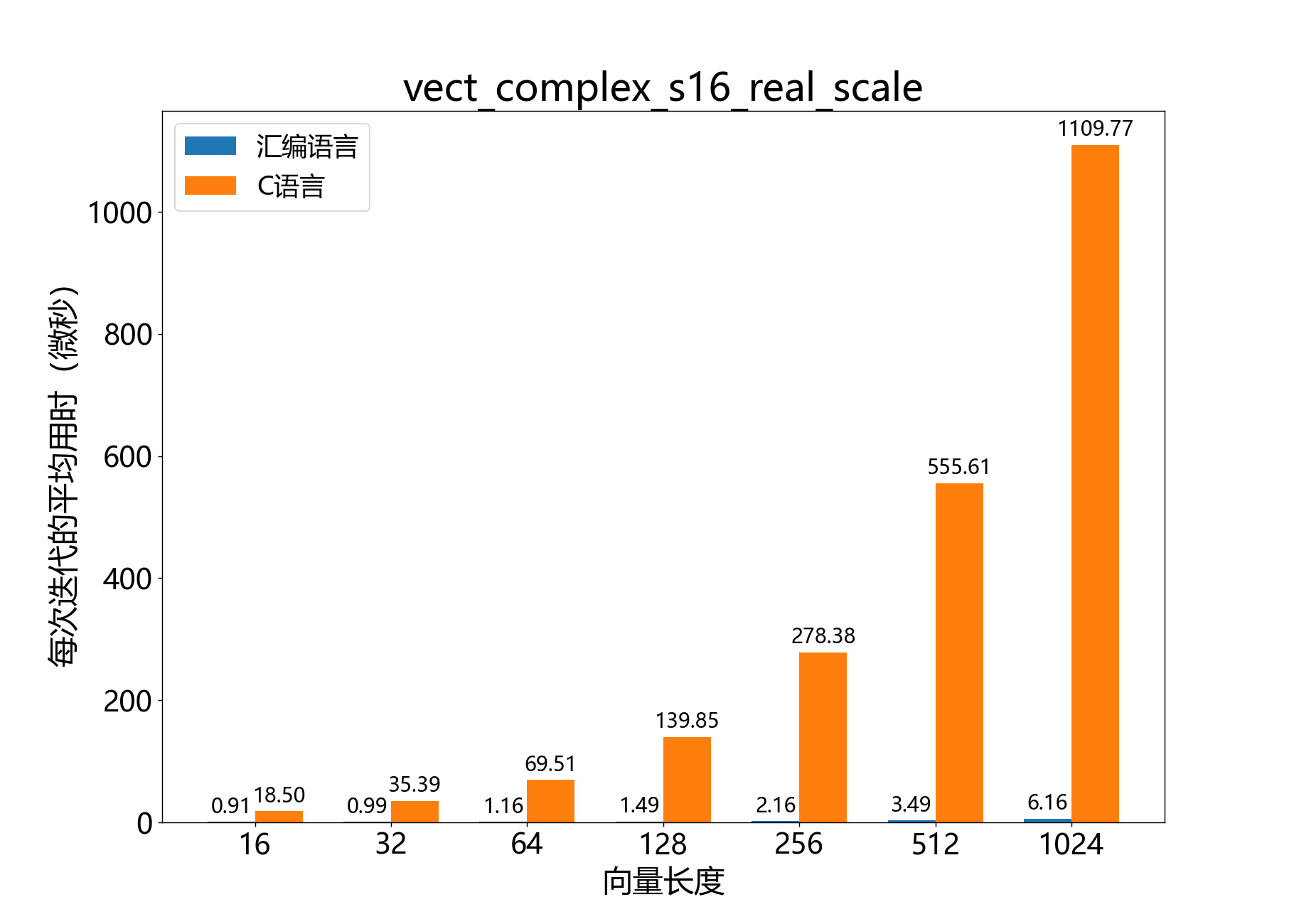
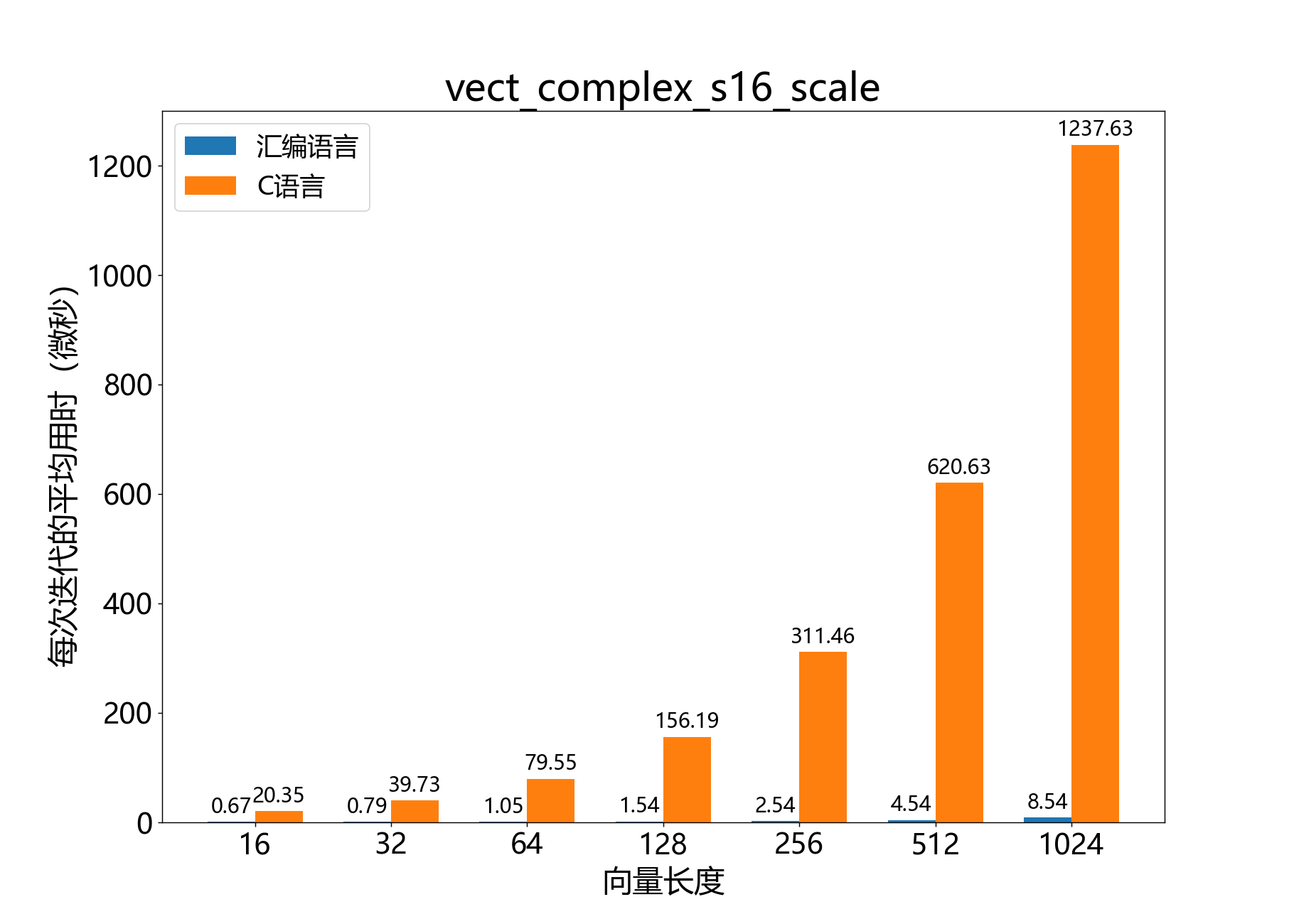
headroom_t vect_complex_s16_scale()
将复数16位向量乘以复数16位标量。
a_real[] 和 a_imag[] 共同表示复数16位输出尾数向量 aˉ。其中 Re{ak} 对应 a_real[k],Im{ak} 对应 a_imag[k]。
b_real[] 和 b_imag[] 共同表示复数16位输入尾数向量 bˉ。其中 Re{bk} 对应 b_real[k],Im{bk} 对应 b_imag[k]。
每个输入向量必须从字对齐的地址开始。这个操作可以在 b_real[] 和 b_imag[] 上安全地原地执行。
c_real 和 c_imag 是复数16位输入尾数 c 的实部和虚部。
length 是向量中的元素数量。
a_shr 是应用于保存倒数第二个结果的32位累加器的无符号算术右移。
该操作由以下方程描述:
vkskRe{ak}Im{ak}=Re{bk}⋅Re{c}−Im{bk}⋅Im{c}=Im{bk}⋅Re{c}+Re{bk}⋅Im{c}=round(sat16(vk⋅2−a_shr))=round(sat16(sk⋅2−a_shr))
其中 k 的取值范围为 0 ... (length−1)。
如果 bˉ 是复数16位BFP向量 bˉ⋅2b_exp 的尾数,并且 c 是浮点值 c⋅2c_exp 的复数16位尾数,则结果向量 aˉ 是BFP向量 aˉ⋅2a_exp 的尾数,其中 a_exp=b_exp+c_exp+a_shr。
函数 vect_complex_s16_scale_prepare() 可以根据输入的指数 b_exp 和 c_exp 以及输入的头空间 b_hr 和 c_hr 来获取 a_exp 和 a_shr 的值。
参数:
-
int16_t a_real[] – [out] 复数输出向量 aˉ 的实部
-
int16_t a_imag[] – [out] 复数输出向量 aˉ 的虚部
-
const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部
-
const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部
-
const int16_t c_real – [in] 复数输入尾数 c 的实部
-
const int16_t c_imag – [in] 复数输入尾数 c 的虚部
-
const unsigned length – [in] 向量 aˉ 和 bˉ 中的元素数量
-
const right_shift_t a_shr – [in] 应用于32位中间结果的右移量
返回值:
异常:
- 如果
a_real、a_imag、b_real、b_imag、c_real 或 c_imag 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐)
参考性能:
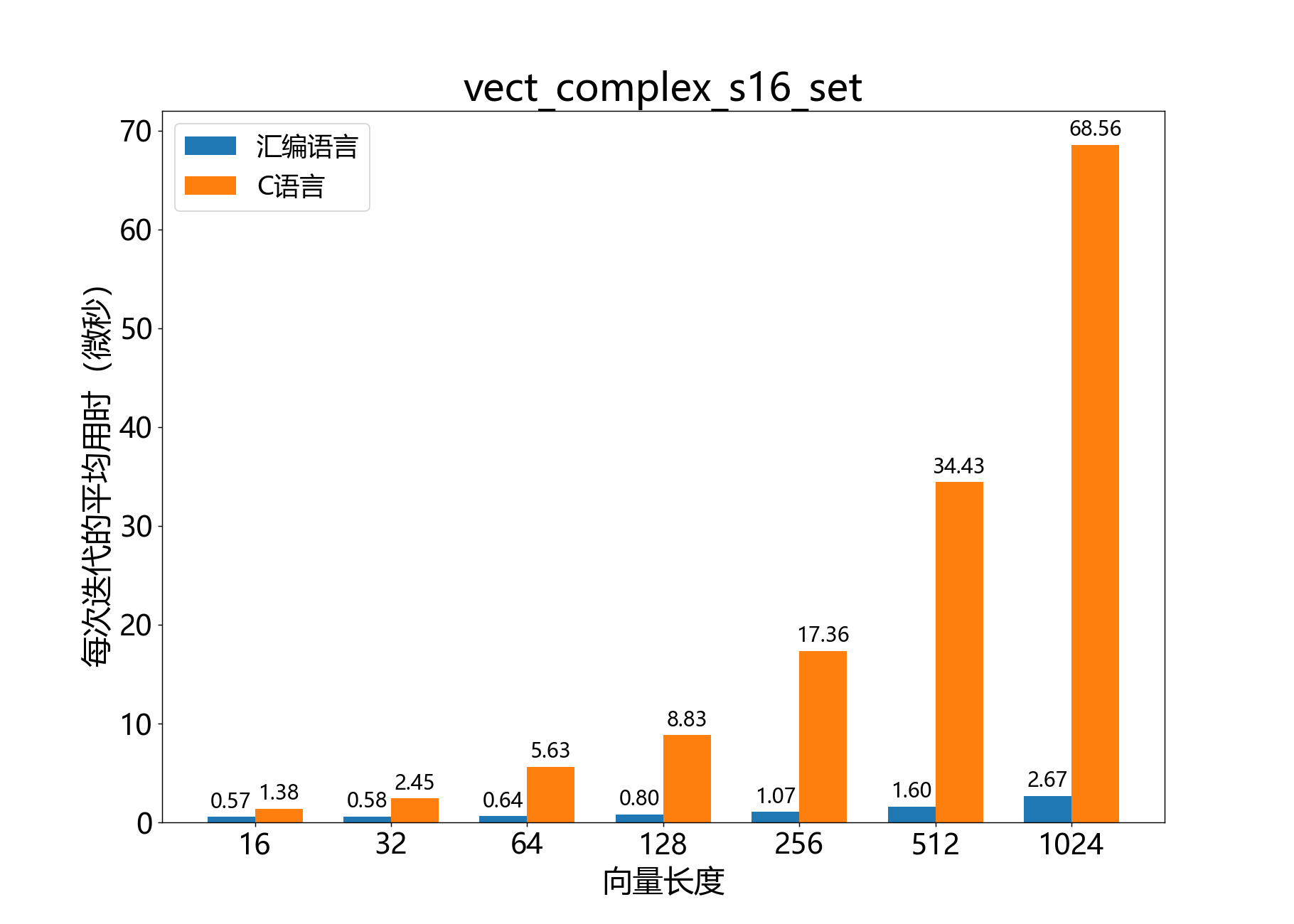
void vect_complex_s16_set()
将复数16位向量的每个元素设置为指定的值。
a_real[] 和 a_imag[] 共同表示复数16位输出尾数向量 aˉ。其中 Re{ak} 是 a_real[k],Im{ak} 是 a_imag[k]。每个向量必须从字对齐的地址开始。
b_real 和 b_imag 是复数16位输入尾数 b 的实部和虚部。每个 a_real[k] 将被设置为 b_real。每个 a_imag[k] 将被设置为 b_imag。
length 是 a_real[] 和 a_imag[] 中的元素数量。
操作:
Re{ak}Im{ak}←Re{b}←Im{b} for k∈0 ... (length−1)
块浮点数:
如果 b 是浮点值 b⋅2b_exp 的尾数,则输出向量 aˉ 是BFP向量 aˉ⋅2a_exp 的尾数,其中 a_exp=b_exp。
参数:
int16_t a_real[] – [out] 复数输出向量 aˉ 的实部int16_t a_imag[] – [out] 复数输出向量 aˉ 的虚部const int16_t b_real – [in] 复数输入标量 b 的实部const int16_t b_imag – [in] 复数输入标量 b 的虚部const unsigned length – [in] 向量 aˉ 和 bˉ 中的元素数量
参考性能:
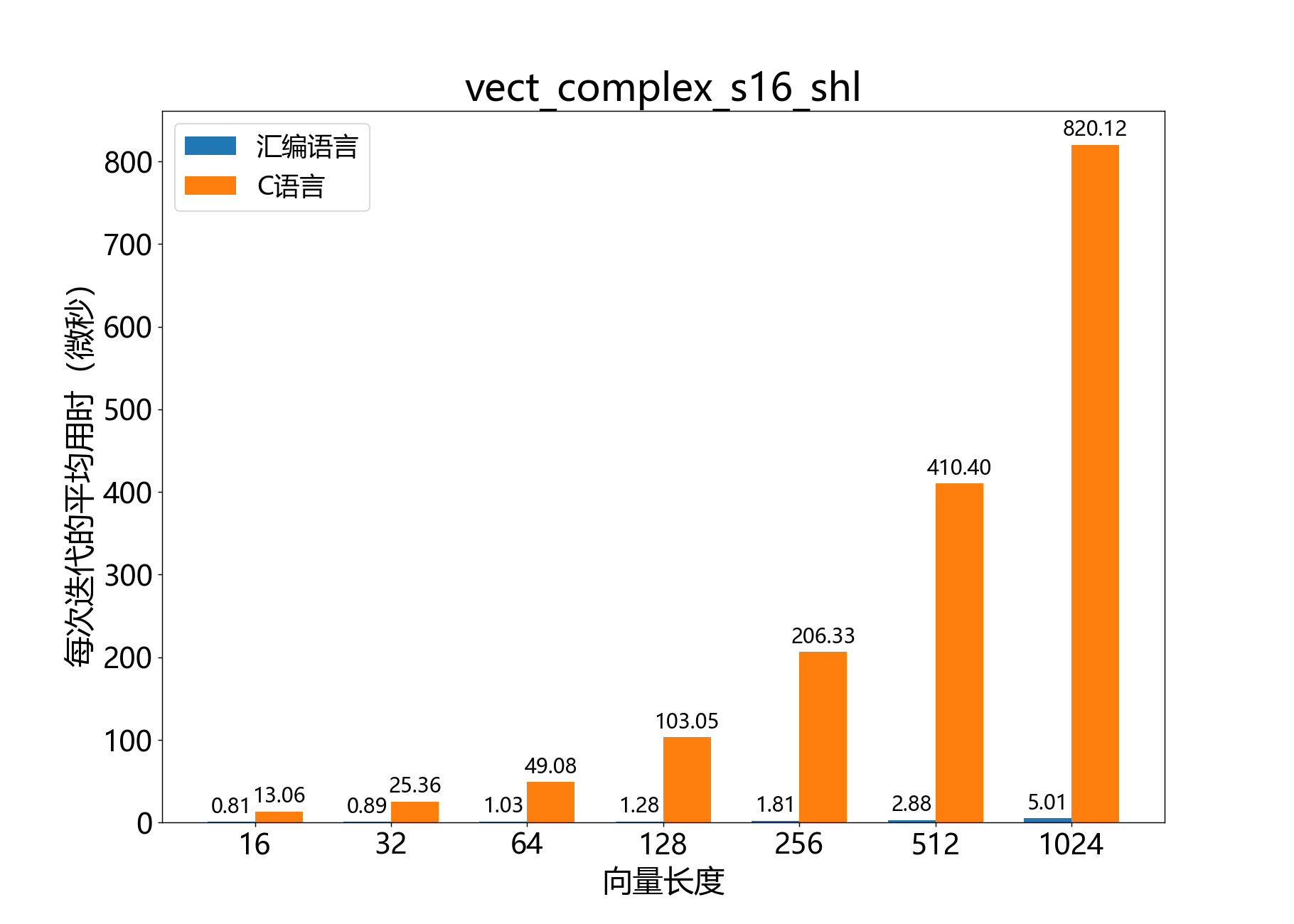
headroom_t vect_complex_s16_shl()
将复数16位向量的每个元素左移指定的位数。
a_real[] 和 a_imag[] 共同表示复数16位输出尾数向量 aˉ。其中 Re{ak} 是 a_real[k],Im{ak} 是 a_imag[k]。
b_real[] 和 b_imag[] 共同表示复数16位输入尾数向量 bˉ。其中 Re{bk} 是 b_real[k],Im{bk} 是 b_imag[k]。
输入向量必须从字对齐的地址开始。此操作可以在输入 b_real[] 和 b_imag[] 上安全地原地执行。
length 是 aˉ 和 bˉ 中的元素数量。
b_shl 是应用于 bˉ 的有符号算术左移。
操作:
Re{ak}←sat16(⌊Re{bk}⋅2b_shl⌋)Im{ak}←sat16(⌊Im{bk}⋅2b_shl⌋) for k∈0 ... (length−1)
块浮点数:
如果 bˉ 是复数16位BFP向量 bˉ⋅2b_exp 的尾数,则结果向量 aˉ 是复数16位BFP向量 aˉ⋅2a_exp 的尾数,其中 aˉ=bˉ⋅2b_shl,a_exp=b_exp。
参数:
int16_t a_real[] – [out] 复数输出向量 aˉ 的实部int16_t a_imag[] – [out] 复数输出向量 aˉ 的虚部const int16_t b_real[] – [in] 复数输入向量 bˉ 的实部const int16_t b_imag[] – [in] 复数输入向量 bˉ 的虚部const unsigned length – [in] 向量 aˉ 和 bˉ 中的元素数量const left_shift_t b_shl – [in] 应用于 bˉ 的左移量
返回值:
headroom_t – 输出向量 aˉ 的头空间
参考性能:
headroom_t vect_complex_s16_shr()
将复合16位向量的每个元素向右移动指定的位数。
a_real[]和a_imag[]一起表示复合16位输出尾数向量 aˉ。每个 Re{ak} 是 a_real[k],每个 Im{ak} 是 a_imag[k]。
b_real[]和b_imag[]一起表示复合16位输入尾数向量 bˉ。每个 Re{bk} 是 b_real[k],每个 Im{bk} 是 b_imag[k]。
输入向量必须从字对齐的地址开始。该操作可以在输入 b_real[] 和 b_imag[] 上安全地原地执行。
length 是 aˉ 和 bˉ 中的元素数量。
b_shr 是应用于 bˉ 的有符号算术右移位数。
操作:
Re{ak}←sat16(⌊Re{bk}⋅2−b_shr⌋)Im{ak}←sat16(⌊Im{bk}⋅2−b_shr⌋) 其中 k∈0 ... (length−1)
块浮点数:
如果 bˉ 是复合16位BFP向量 bˉ⋅2b_exp 的尾数,则结果向量 aˉ 是复合16位BFP向量 aˉ⋅2a_exp 的尾数,其中 aˉ=bˉ⋅2−b_shr,a_exp=b_exp。
参数:
int16_t a_real[] – [out] 复合输出向量 aˉ 的实部int16_t a_imag[] – [out] 复合输出向量 aˉ 的虚部const int16_t b_real[] – [in] 复合输入向量 bˉ 的实部const int16_t b_imag[] – [in] 复合输入向量 bˉ 的虚部const unsigned length – [in] 向量 aˉ 和 bˉ 的元素数量const right_shift_t b_shr – [in] 应用于 bˉ 的右移位数
返回值:
异常:
- ET_LOAD_STORE 如果
a_real、a_imag、b_real 或 b_imag 不是字对齐的,将引发该异常。
参考性能:
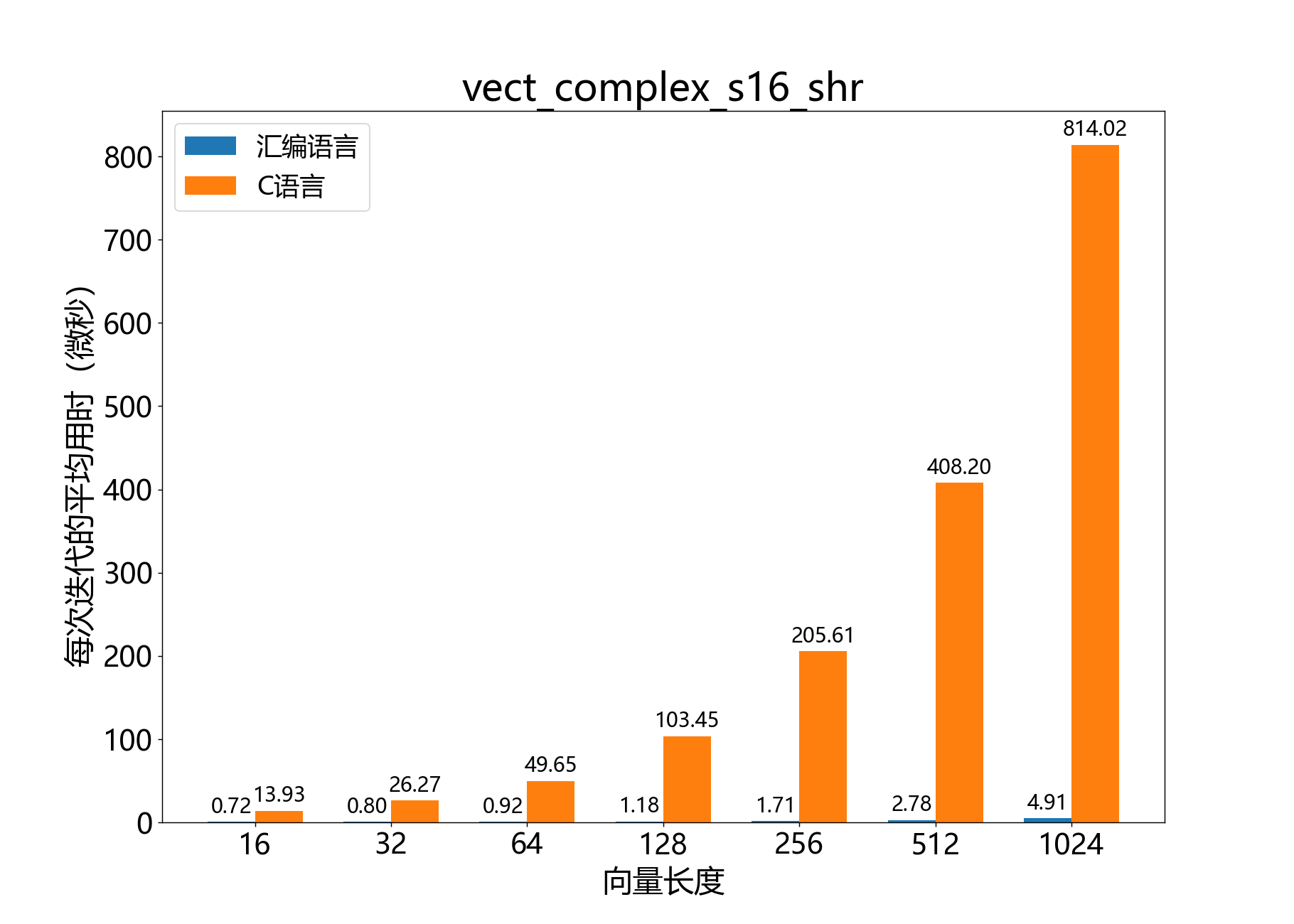
headroom_t vect_complex_s16_squared_mag()
获取复合16位向量元素的平方幅值。
a[] 表示实部16位输出尾数向量 aˉ。
b_real[] 和 b_imag[] 一起表示复合16位输入尾数向量 bˉ。每个 Re{bk} 是 b_real[k],每个 Im{bk} 是 b_imag[k]。
输入向量必须从字对齐的地址开始。
length 是向量 aˉ 和 bˉ 中的元素数量。
a_shr 是应用于保存倒数第二个结果的32位累加器的无符号算术右移位数。
操作:
ak←((Re{bk′})2+(Im{bk′})2)⋅2−a_shr 其中 k∈0 ... (length−1)
块浮点数:
如果 bˉ 是复合16位BFP向量 bˉ⋅2b_exp 的尾数,则结果向量 aˉ 是实部16位BFP向量 aˉ⋅2a_exp 的尾数,其中 a_exp=2⋅b_exp+a_shr。
函数 vect_complex_s16_squared_mag_prepare() 可以根据输入指数 b_exp 和头空间 b_hr 获取 a_exp 和 a_shr 的值。
参数:
int16_t a[] – [out] 实部输出向量 aˉconst int16_t b_real[] – [in] 复合输入向量 bˉ 的实部const int16_t b_imag[] – [in] 复合输入向量 bˉ 的虚部const unsigned length – [in] 向量 aˉ 和 bˉ 中的元素数量const right_shift_t a_shr – [in] 应用于32位中间结果的右移位数
异常:
- ET_LOAD_STORE 如果
a、b_real 或 b_imag 不是字对齐的,将引发该异常。
参见:
vect_complex_s16_squared_mag_prepare
参考性能:

headroom_t vect_s32_abs()
计算32位向量的逐元素绝对值。
a[]和b[]分别表示32位向量aˉ和bˉ。每个向量必须从字对齐的地址开始。此操作可以安全地原地执行在b[]上。
length是向量中的元素数量。
操作:
ak←sat32(∣bk∣)对于k∈0 ... (length−1)
块浮点数:
如果bˉ是BFP向量bˉ⋅2b_exp的尾数,则输出向量aˉ是BFP向量aˉ⋅2a_exp的尾数,其中a_exp=b_exp。
参数:
int32_t a[] – [out] 输出向量aˉconst int32_t b[] – [in] 输入向量bˉconst unsigned length – [in] 向量aˉ和bˉ中的元素数量
返回值: 输出向量aˉ的头空间。
异常: 如果a或b不是字对齐的(参见 笔记:向量对齐),则引发ET_LOAD_STORE异常。
相关文档: vect_s32_abs_prepare
参考性能:
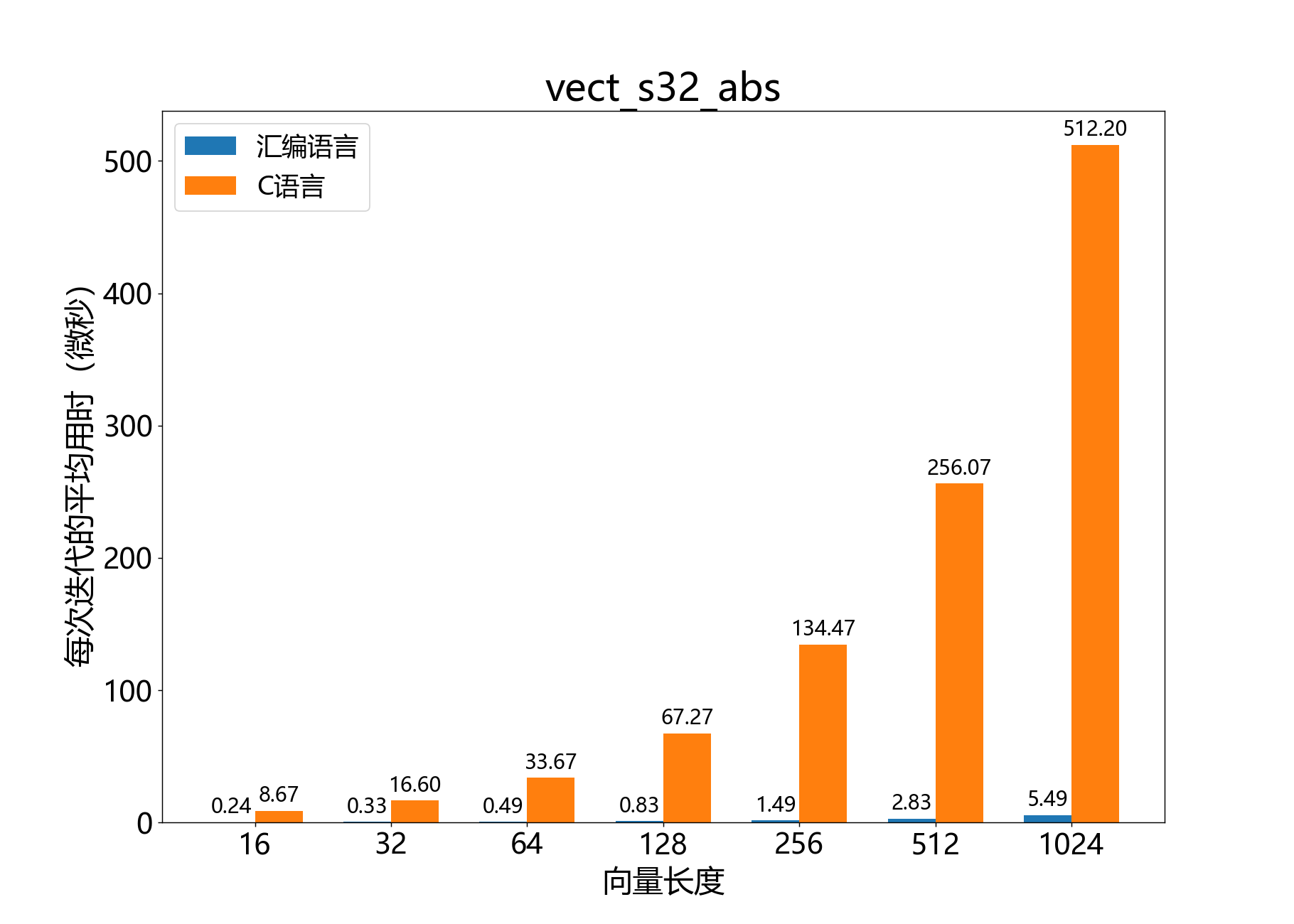
headroom_t vect_complex_s16_sub()
从一个复数16位向量中减去另一个复数16位向量。
a_real[]和a_imag[]一起表示复数16位输出尾数向量aˉ。每个Re{ak}是a_real[k],每个Im{ak}是a_imag[k]。
b_real[]和b_imag[]一起表示复数16位输入尾数向量bˉ。每个Re{bk}是b_real[k],每个Im{bk}是b_imag[k]。
c_real[]和c_imag[]一起表示复数16位输入尾数向量cˉ。每个Re{ck}是c_real[k],每个Im{ck}是c_imag[k]。
输入向量的每个元素必须从字对齐的地址开始。此操作可以在输入b_real[]、b_imag[]、c_real[]和c_imag[]上安全地原地执行。
length是向量中的元素数量。
b_shr和c_shr是应用于bˉ和cˉ的有符号算术右移。
操作:
bk′←sat16(⌊bk⋅2−b_shr⌋)ck′←sat16(⌊ck⋅2−c_shr⌋)Re{ak}←Re{bk′}−Re{ck′}Im{ak}←Im{bk′}−Im{ck′}对于k∈0 ... (length−1)
块浮点数:
如果bˉ和cˉ是BFP向量bˉ⋅2b_exp和cˉ⋅2c_exp的复数16位尾数,则结果向量aˉ是BFP向量aˉ⋅2a_exp的复数16位尾数。
在此情况下,必须选择b_shr和c_shr,使得a_exp=b_exp+b_shr=c_exp+c_shr。只有当尾数关联到相同的指数时,才有加法或减法的意义。
函数vect_complex_s16_sub_prepare()可以根据输入指数b_exp和c_exp以及输入头空间b_hr和c_hr来获取a_exp、b_shr和c_shr的值。
参数:
int16_t a_real[] – [out] 复数输出向量aˉ的实部int16_t a_imag[] – [out] 复数输出向量aˉ的虚部const int16_t b_real[] – [in] 复数输入向量bˉ的实部const int16_t b_imag[] – [in] 复数输入向量bˉ的虚部const int16_t c_real[] – [in] 复数输入向量cˉ的实部const int16_t c_imag[] – [in] 复数输入向量cˉ的虚部const unsigned length – [in] 向量aˉ、bˉ和cˉ中的元素数量const right_shift_t b_shr – [in] 应用于bˉ的右移const right_shift_t c_shr – [in] 应用于cˉ的右移
返回值:
异常:
- 如果
a_real、a_imag、b_real、b_imag、c_real或c_imag不是字对齐的,则引发ET_LOAD_STORE异常。 参见笔记:向量对齐。
相关文档: vect_complex_s16_sub_prepare
参考性能:
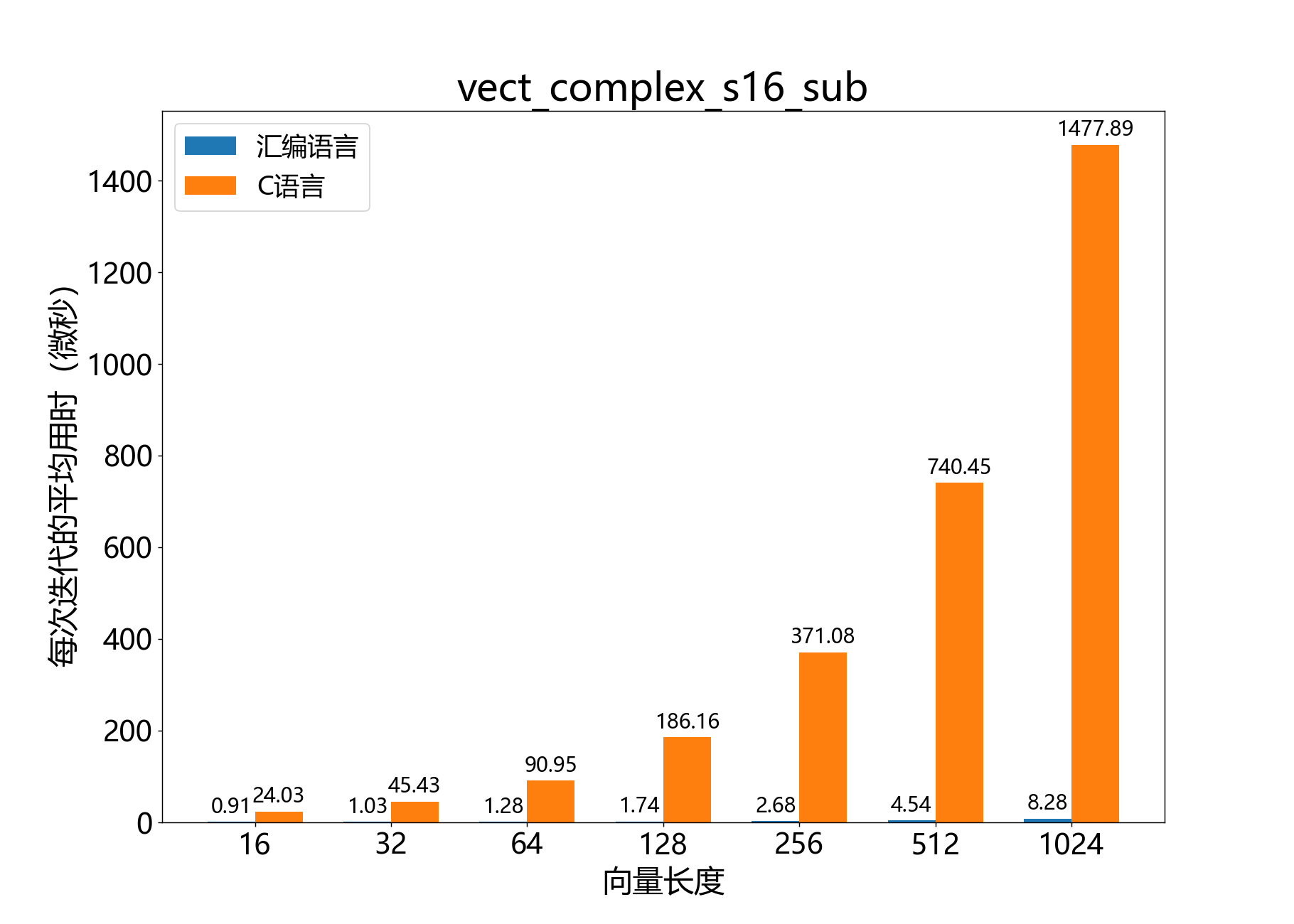
complex_s32_t vect_complex_s16_sum()
获取复数16位向量的元素和。
b_real[]和b_imag[]一起表示复数16位输入尾数向量bˉ,并且必须从字对齐的地址开始。每个Re{bk}是b_real[k],每个Im{bk}是b_imag[k]。
length是向量bˉ中的元素数量。
操作:
Re{a}←k=0∑length−1(Re{bk})Im{a}←k=0∑length−1(Im{bk})
块浮点数:
如果bˉ是BFP向量bˉ⋅2b_exp的尾数,则返回的值a是浮点值a⋅2a_exp的复数32位尾数,其中a_exp=b_exp。
参数:
const int16_t b_real[] – [in] 复数输入向量bˉ的实部const int16_t b_imag[] – [in] 复数输入向量bˉ的虚部const unsigned length – [in] 向量bˉ中的元素数量
返回值:
异常:
- 如果
b_real或b_imag不是字对齐的,则引发ET_LOAD_STORE异常。 参见笔记:向量对齐。
参考性能:
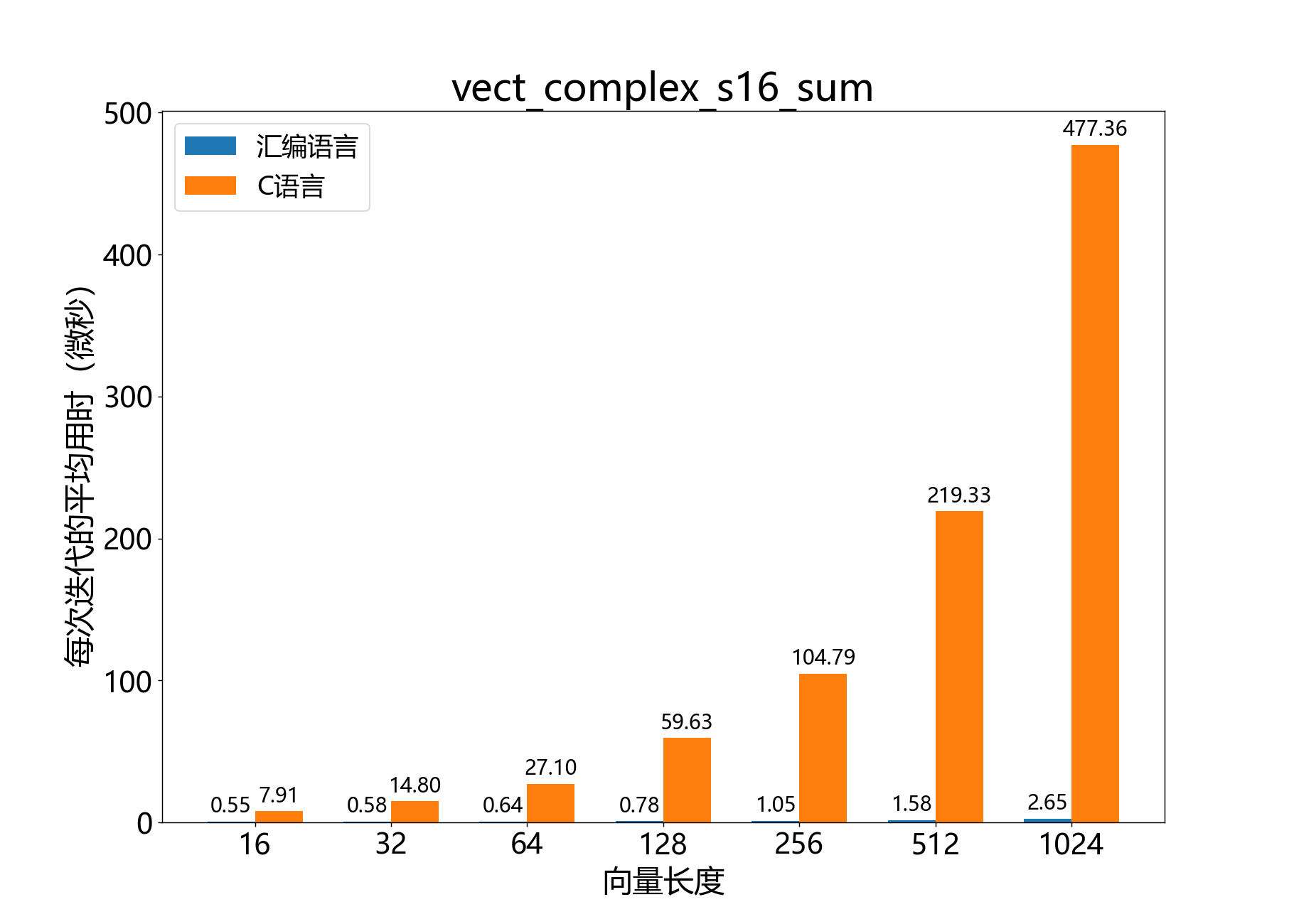
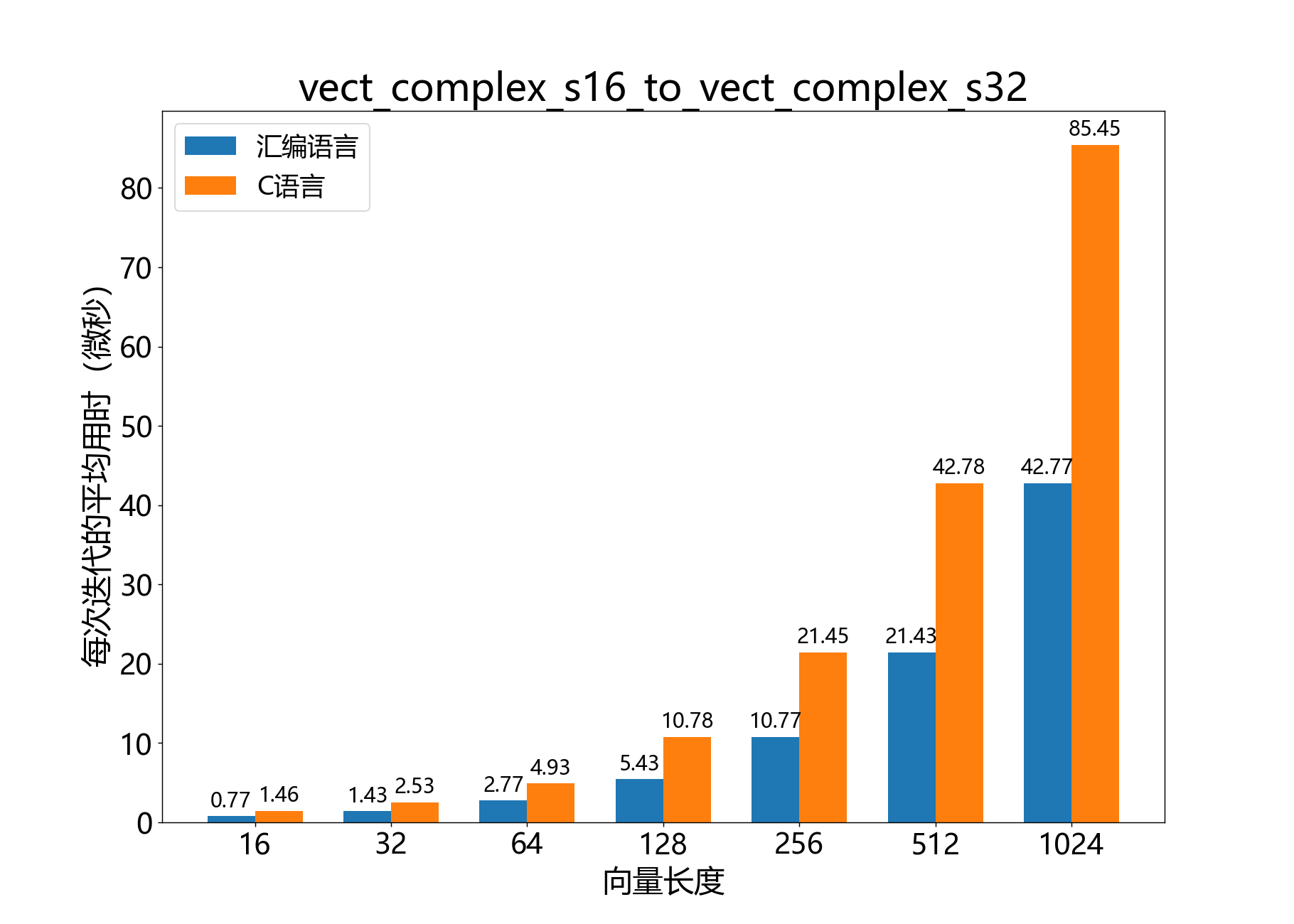
void vect_complex_s16_to_vect_complex_s32()
将复数16位向量转换为复数32位向量。
a[]表示复数32位输出向量aˉ。它必须从双字(8字节)对齐的地址开始。
b_real[]和b_imag[]一起表示复数16位输入尾数向量bˉ。每个Re{bk}是b_real[k],每个Im{bk}是b_imag[k]。
参数length是每个向量中的元素数量。
操作:
Re{ak}←Re{bk}Im{ak}←Im{bk}对于k∈0 ... (length−1)
块浮点数:
如果bˉ是BFP向量bˉ⋅2b_exp的复数16位尾数,则结果向量aˉ是BFP向量aˉ⋅2a_exp的复数32位尾数,其中a_exp=b_exp。
注意事项:
- 此函数不返回输出向量aˉ的头空间。输出的头空间始终比输入的头空间大16位。
参数:
complex_s32_t a[] – [out] 复数输出向量aˉ。const int16_t b_real[] – [in] 复数输入向量bˉ的实部。const int16_t b_imag[] – [in] 复数输入向量bˉ的虚部。const unsigned length – [in] 向量aˉ和bˉ中的元素数量。
异常:
- 如果
a不是双字对齐的,则引发ET_LOAD_STORE异常。 参见笔记:向量对齐。
参考性能: