Skip to main content
欢迎来到PAWPAW技术文档网站，了解更多信息。

16-Bit Vector API

#define VECT_SQRT_S16_MAX_DEPTH​

vect_s16_sqrt() 可以计算的最大比特深度。

取值:

15

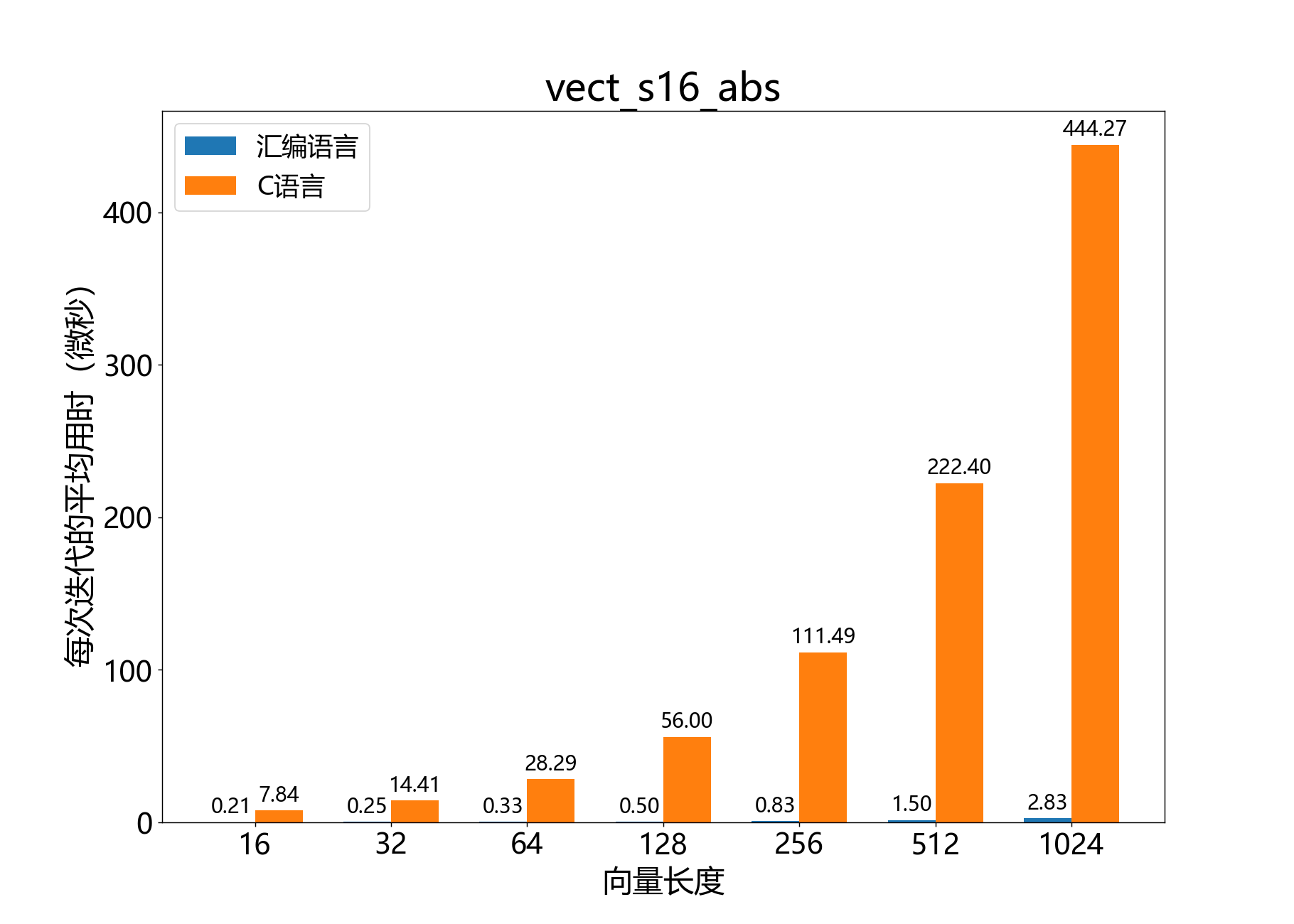
headroom_t vect_s16_abs()​

计算一个16位向量的逐元素绝对值。

参数:

  • int16_t a[] – [out] 输出向量 aa
  • const int16_t b[] – [in] 输入向量 bb
  • const unsigned length – [in] 向量 aa 和 bb 的元素数量

返回值: 输出向量 aa 的头空间。

异常:

  • ET_LOAD_STORE：如果 a 或 b 不是字对齐。

参考性能:

vect_s16_abs

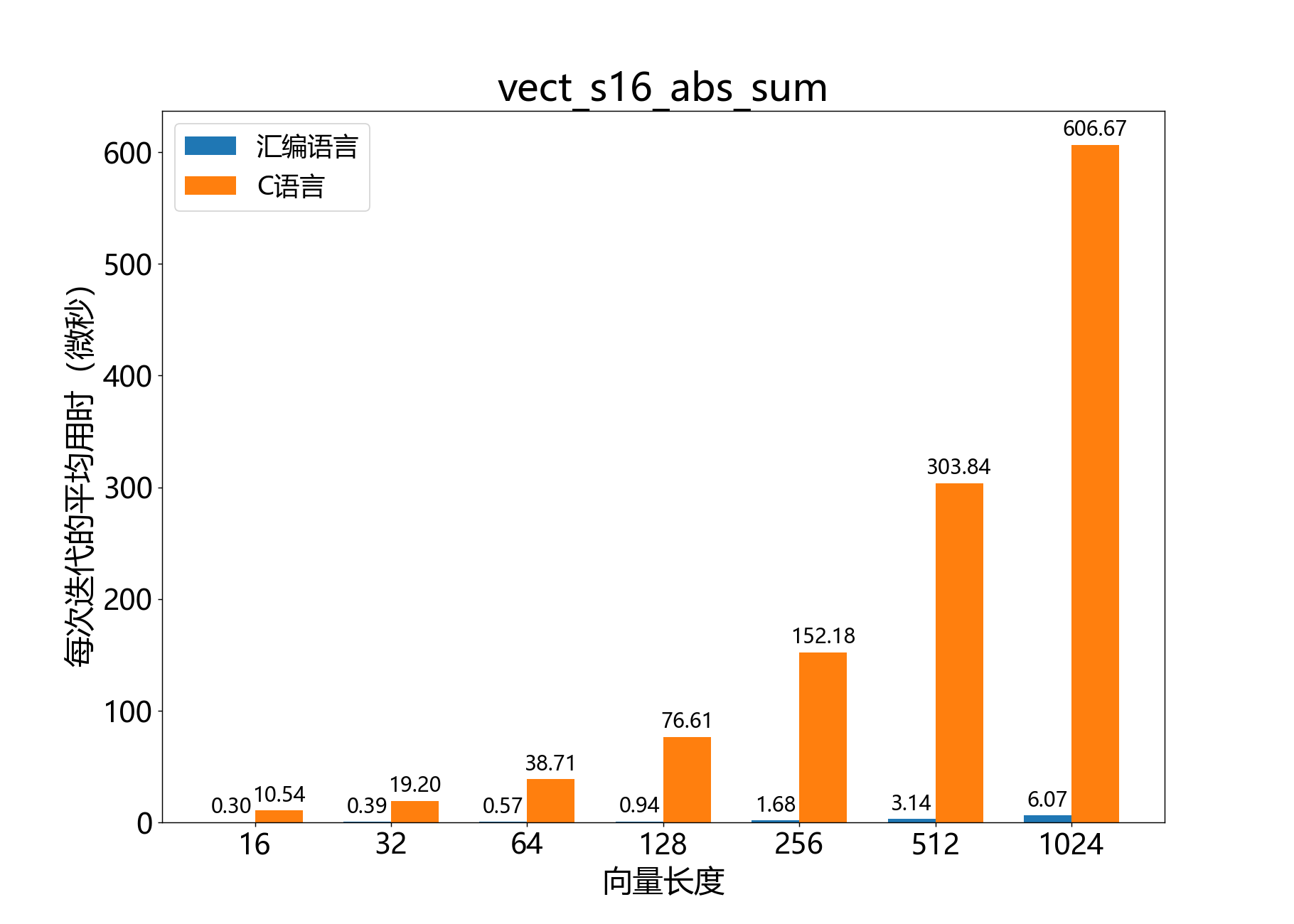
int32_t vect_s16_abs_sum()​

计算一个16位向量各元素绝对值之和。

参数:

  • const int16_t b[] – [in] 输入向量 bb
  • const unsigned length – [in] 向量 bb 的元素数量

返回值: 32位求和值 aa。

异常:

  • ET_LOAD_STORE：如果 b 不是字对齐。

参考性能:

vect_s16_abs_sum

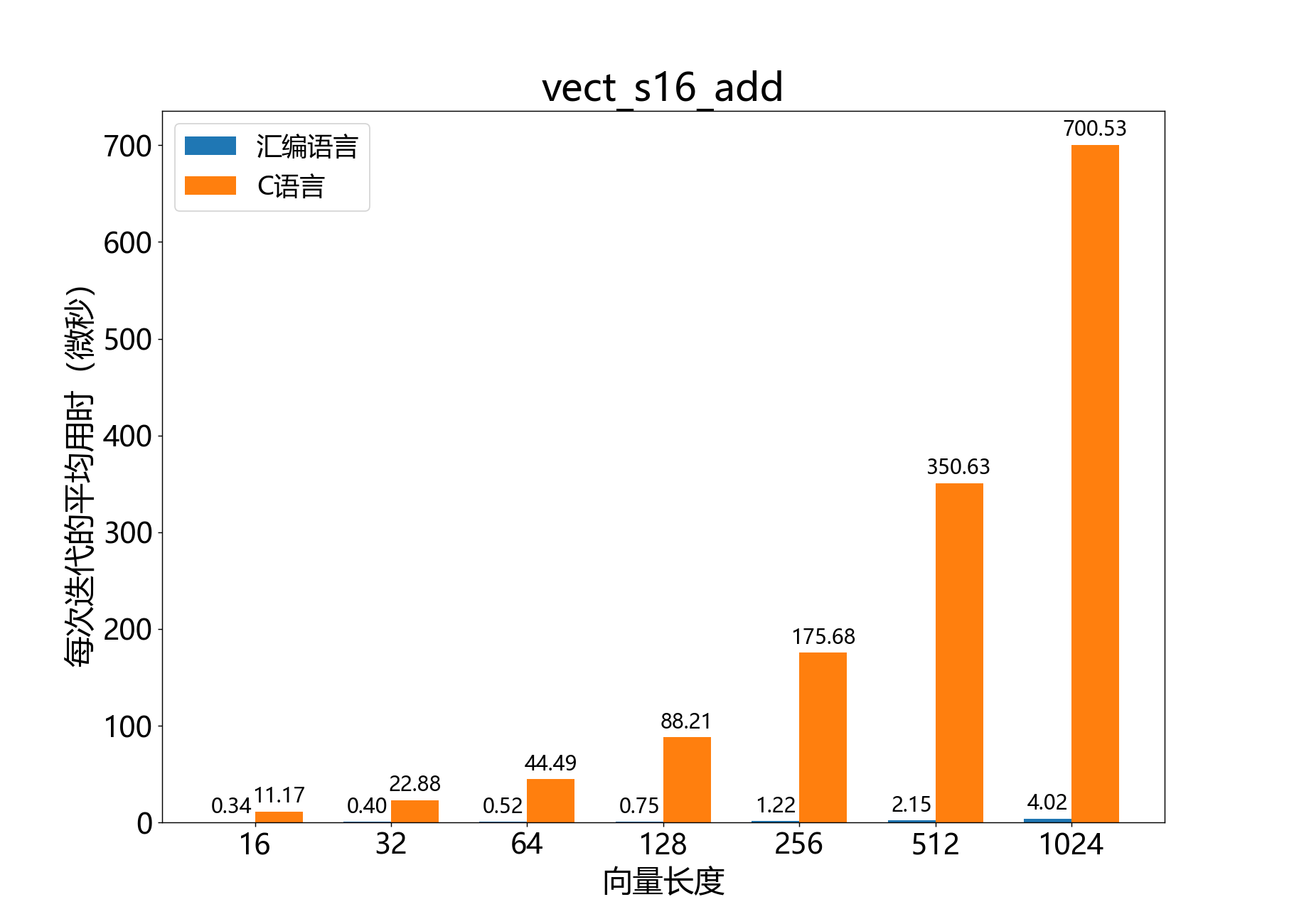
headroom_t vect_s16_add()​

将一个16位BFP向量与另一个相加。

参数:

  • int16_t a[] – [out] 输出向量 aa
  • const int16_t b[] – [in] 输入向量 bb
  • const int16_t c[] – [in] 输入向量 cc
  • const unsigned length – [in] 向量 aa、bb 和 cc 的元素数量
  • const right_shift_t b_shr – [in] 应用于 bb 的右移位数
  • const right_shift_t c_shr – [in] 应用于 cc 的右移位数

返回值: 输出向量 aa 的头空间。

异常:

  • ET_LOAD_STORE：如果 a、b 或 c 不是字对齐。

参考性能:

vect_s16_add

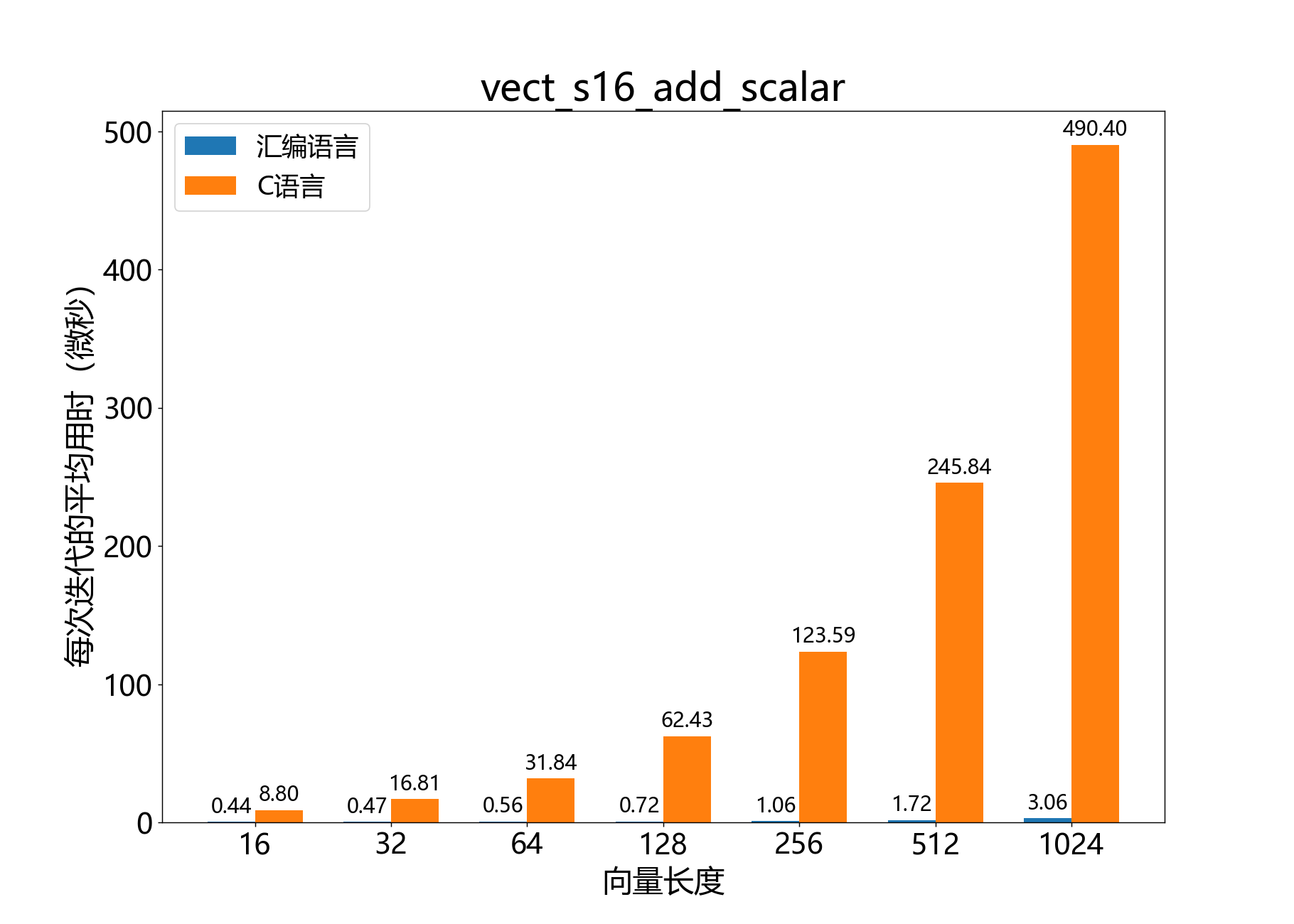
headroom_t vect_s16_add_scalar()​

将标量加到一个16位向量中。

参数:

  • int16_t a[] – [out] 输出向量 aa
  • const int16_t b[] – [in] 输入向量 bb
  • const int16_t c – [in] 输入标量 cc
  • const unsigned length – [in] 向量 aa 和 bb 的元素数量
  • const right_shift_t b_shr – [in] 应用于 bb 的右移位数

返回值: 输出向量 aa 的头空间。

异常:

  • ET_LOAD_STORE：如果 a 或 b 不是字对齐。

参考性能:

vect_s16_add_scalar

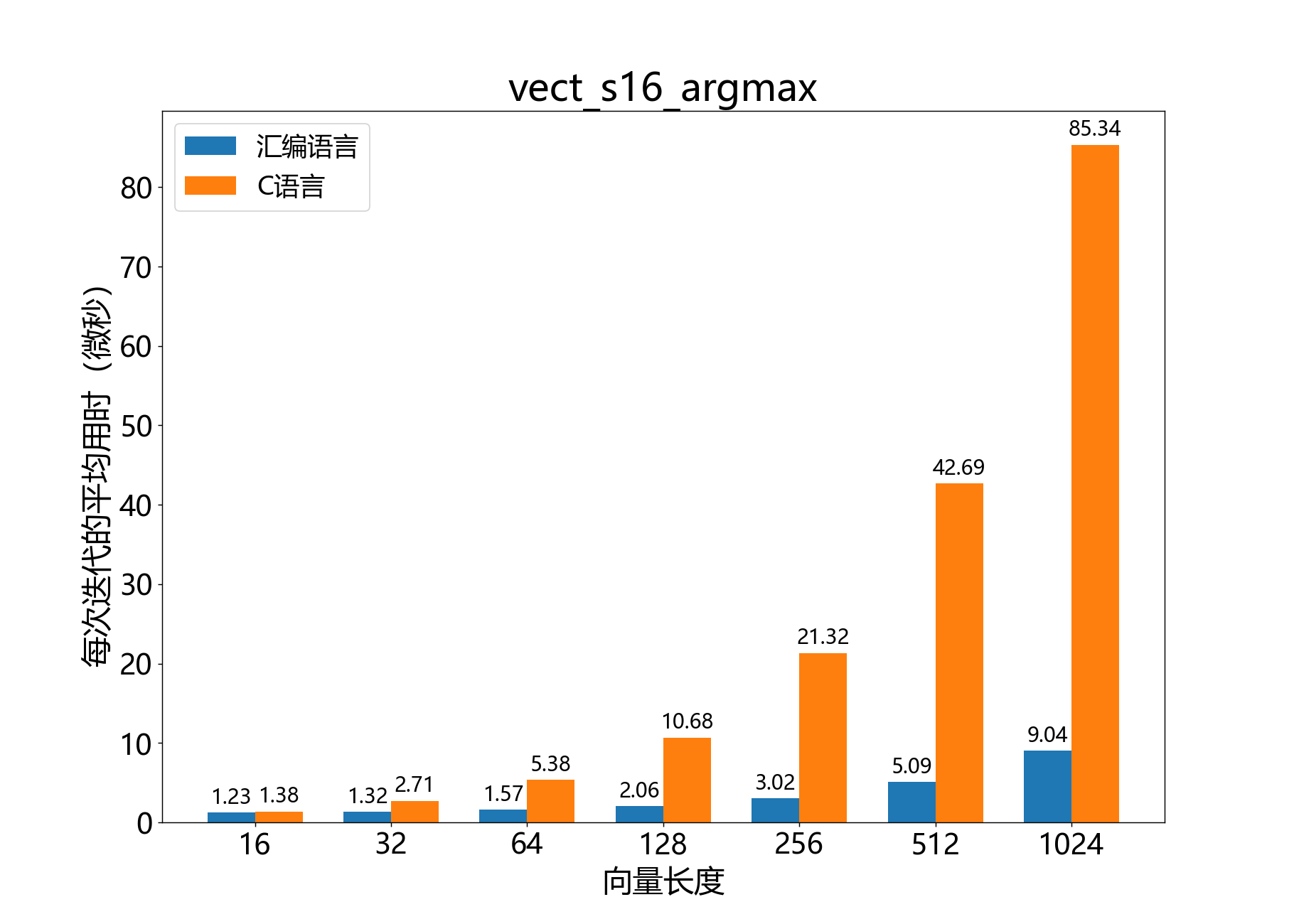
unsigned vect_s16_argmax()​

获取16位向量中最大元素的数组索引。

b[]表示16位输入向量 bˉ\bar{b}。它必须从字对齐的地址开始。

length是 bˉ\bar{b} 中的元素数量。

操作: a←argmaxk{bk}其中 k∈0 ... (length−1)a \leftarrow argmax_k\{ b_k \} \\ \qquad\text{其中} \ k\in 0\ ...\ (length-1)

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const unsigned length – [in] 向量 bˉ\bar{b} 中的元素数量

返回值:

向量 bˉ\bar{b} 的最大元素的索引 aa。如果存在多个最大值，则返回最小索引。

异常:

参考性能:

vect_s16_argmax

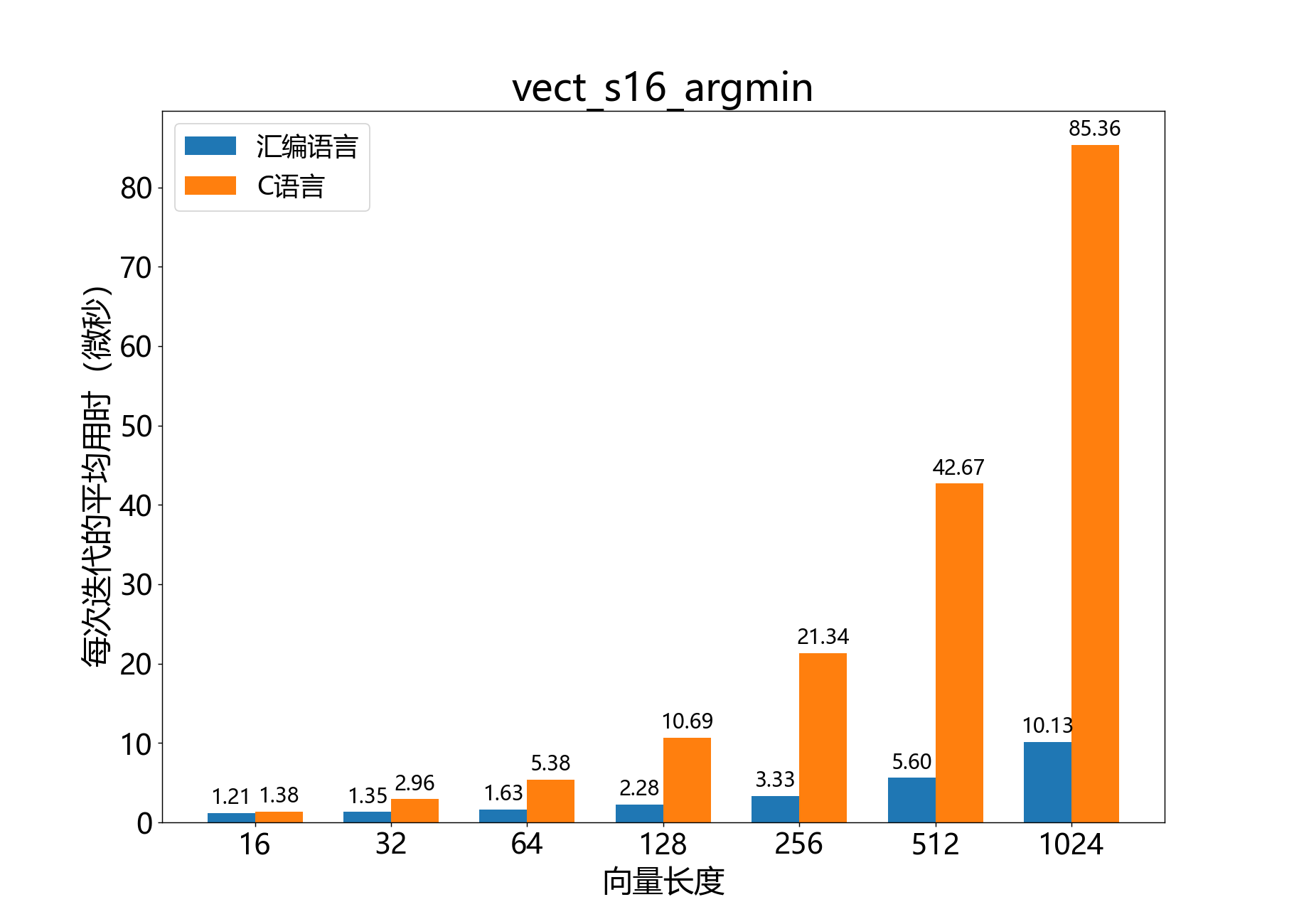
unsigned vect_s16_argmin()​

获取16位向量中最小元素的数组索引。

b[]表示16位输入向量 bˉ\bar{b}。它必须从字对齐的地址开始。

length是 bˉ\bar{b} 中的元素数量。

操作:

a←argmink{bk}其中 k∈0 ... (length−1)a \leftarrow argmin_k\{ b_k \} \\ \qquad\text{其中} \ k\in 0\ ...\ (length-1)

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const unsigned length – [in] 向量 bˉ\bar{b} 中的元素数量

返回值:

向量 bˉ\bar{b} 的最小元素的索引 aa。如果存在多个最小值，则返回最小索引。

异常:

参考性能:

vect_s16_argmin

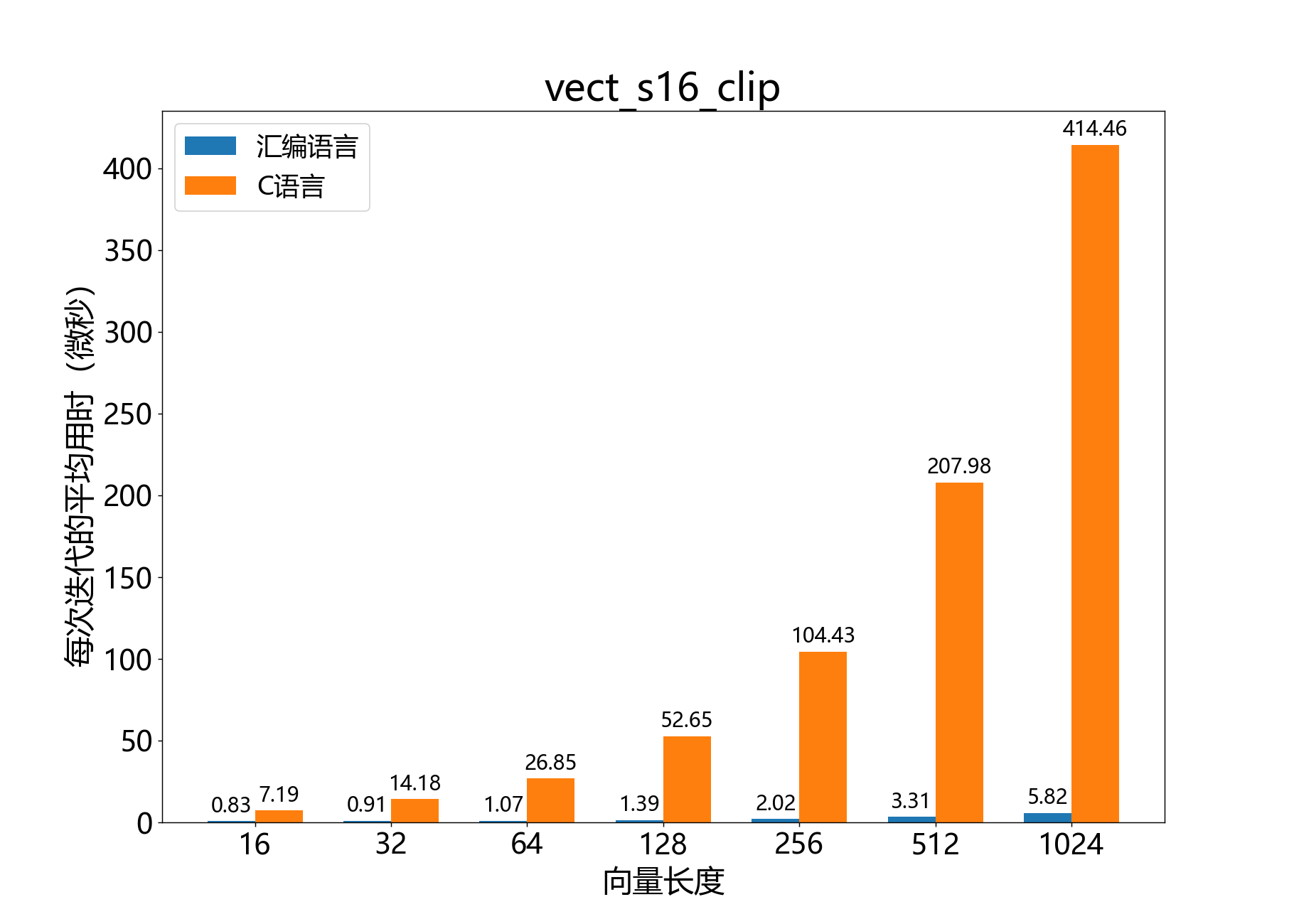
headroom_t vect_s16_clip()​

将16位向量的元素截取到指定范围。

a[]和b[]分别表示16位向量 aˉ\bar{a} 和 bˉ\bar{b}。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行。

length是每个向量中的元素数量。

lower_bound和upper_bound分别是截取范围的下界和上界。这些边界仅在应用 b_shr 之后才与 bˉ\bar{b} 的每个元素进行比较。

b_shr 是应用于 bˉ\bar{b} 元素之前的带符号算术右移位数。

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则输出BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的指数 a_expa\_exp 由 a_exp=b_exp+b_shra\_exp = b\_exp + b\_shr 给出。

操作:

bk′←sat16(⌊bk⋅2−b_shr⌋)ak←{lower_boundbk′≤lower_boundupper_boundbk′≥upper_boundbk′otherwise其中 k∈0 ... (length−1)\begin{align*} b_k' & \leftarrow sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ a_k & \leftarrow \begin{cases} lower\_bound & b_k' \le lower\_bound \\ upper\_bound & b_k' \ge upper\_bound \\ b_k' & \text{otherwise} \end{cases} \end{align*} \qquad\text{其中} \ k\in 0\ ...\ (length-1)

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则输出向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_exp+b_shra\_exp = b\_exp + b\_shr。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const unsigned length – [in] 向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量

  • const int16_t lower_bound – [in] 截取范围的下界

  • const int16_t upper_bound – [in] 截取范围的上界

  • const right_shift_t b_shr – [in] 应用于 bˉ\bar{b} 元素之前的算术右移位数

返回值:

输出向量 aˉ\bar{a} 的头空间

异常:

参考性能:

vect_s16_clip

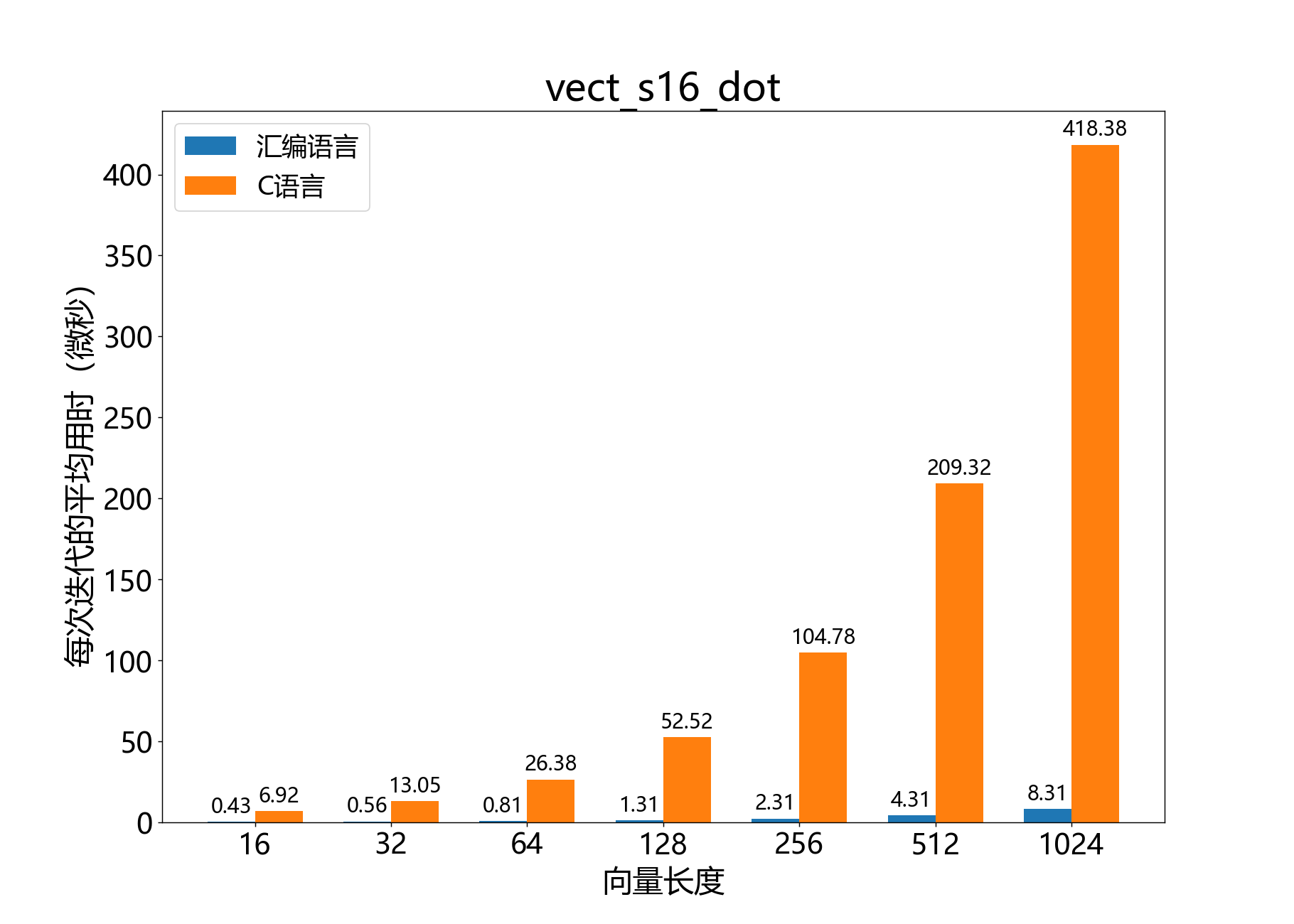
int64_t vect_s16_dot()​

计算两个16位向量的内积。

b[]和c[]分别表示32位向量 aˉ\bar{a} 和 bˉ\bar{b}。每个向量必须从字对齐的地址开始。

length是每个向量中的元素数量。

操作:

a←∑k=0length−1(bk⋅ck)a \leftarrow \sum_{k=0}^{length-1}\left( b_k \cdot c_k \right)

块浮点数:

如果 bˉ\bar{b} 和 cˉ\bar{c} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 和 cˉ⋅2c_exp\bar{c}\cdot 2^{c\_exp} 的尾数，则结果 aa 是结果 a⋅2a_expa \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_exp+c_expa\_exp = b\_exp + c\_exp。

如果需要，可以将 aa 的位深度降低到16位或32位，得到新的结果 a′⋅2a_exp′a' \cdot 2^{a\_exp'}，其中 a′=a⋅2−a_shra' = a \cdot 2^{-a\_shr} 且 a_exp′=a_exp+a_shra\_exp' = a\_exp + a\_shr。

注意事项:

和 aa 相加的和同时累积到16个48位累加器中，最后在最后一步将它们相加。只要 length 小于大约200万，结果的溢出或饱和是不可能的。

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const int16_t c[] – [in] 输入向量 cˉ\bar{c}

  • const unsigned length – [in] 向量 bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量

返回值:

  • aa，向量 bˉ\bar{b} 和 cˉ\bar{c} 的内积。

异常:

参考性能:

vect_s16_dot

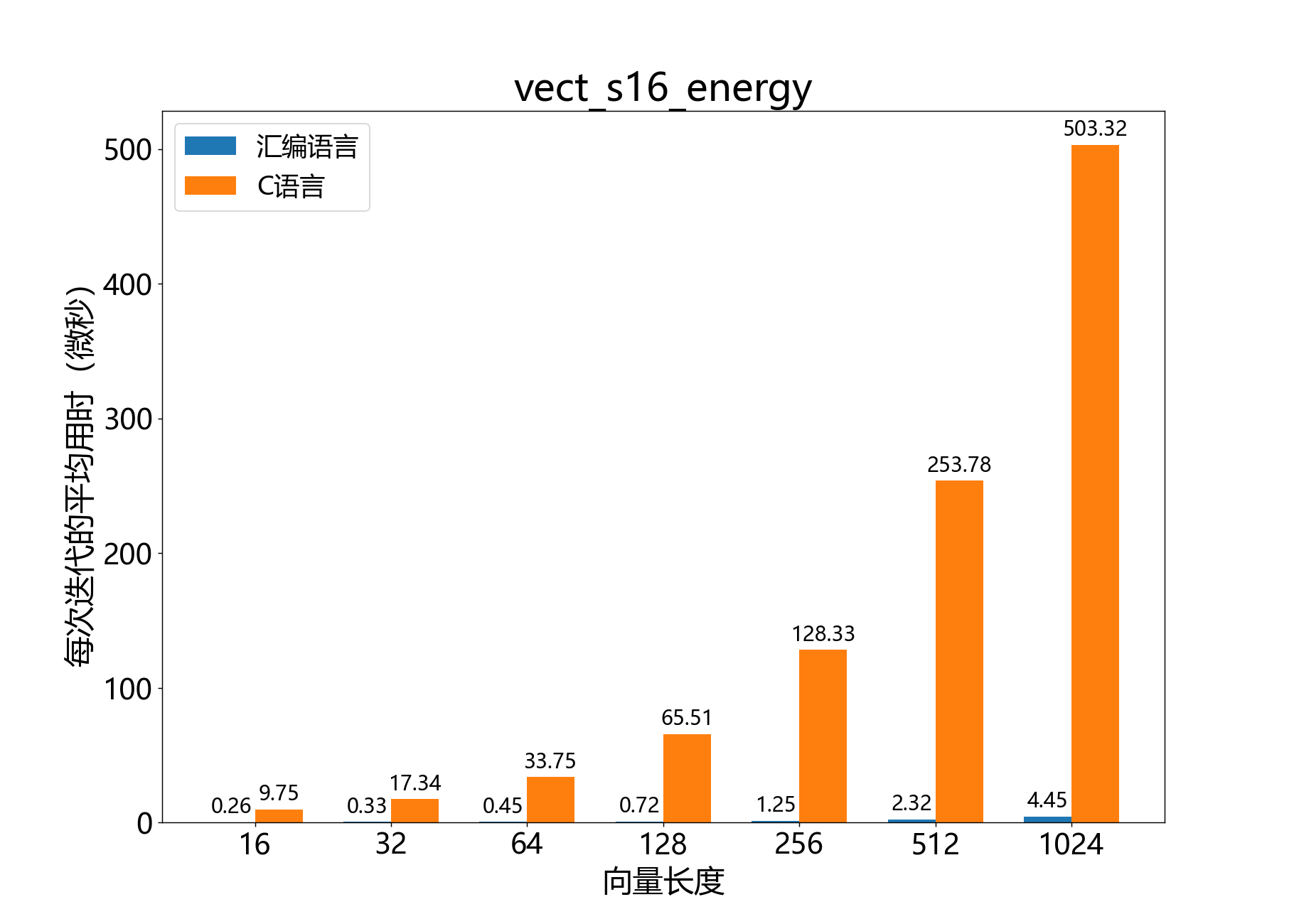
int32_t vect_s16_energy()​

计算16位向量的能量（元素平方和）。

b[]表示16位向量 bˉ\bar{b}。b[] 必须从字对齐的地址开始。

length是 bˉ\bar{b} 中的元素数量。

b_shr 是应用于 bˉ\bar{b} 元素的带符号算术右移。应选择适当的 b_shr，以避免饱和的可能性。请参阅下面的注意事项。

操作:

bk′←sat16(⌊bk⋅2−b_shr⌋)a←∑k=0length−1(bk′)2\begin{align*} b_k' &\leftarrow sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ a &\leftarrow \sum_{k=0}^{length-1} (b_k')^2 \end{align*}

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则浮点结果是 a⋅2a_expa \cdot 2^{a\_exp}，其中32位尾数 aa 由此函数返回，a_exp=2⋅(b_exp+b_shr)a\_exp = 2 \cdot (b\_exp + b\_shr)。

其他细节:

如果 bˉ\bar{b} 具有 b_hrb\_hr 位的头空间，则每个乘积 (bk′)2(b_k')^2 的最大值为 230−2⋅(b_hr+b_shr)2^{30 - 2 \cdot (b\_hr + b\_shr)}。只要 length 小于 1+2⋅(b_hr+b_shr)1 + 2\cdot (b\_hr + b\_shr)，就不应出现此类错误。将 b_shrb\_shr 增加 11，每次增加 11，可以使可以求和的元素数量翻倍，而不会溢出的风险。

如果调用者的尾数向量比这个更长，可以通过在输入的子序列上多次调用此函数以获取部分结果，并在用户代码中将结果相加来找到完整的结果。

在许多情况下，调用者可能有先验知识表明饱和是不可能的（或非常接近），在这种情况下，可以忽略此准则。然而，这些情况是特定于应用程序的，并且远远超出了本文档的范围，因此留给用户自行决定。

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const unsigned length – [in] 向量 bˉ\bar{b} 中的元素数量

  • const right_shift_t b_shr – [in] 应用于 bˉ\bar{b} 的右移位数

返回值:

  • 向量 bˉ\bar{b} 的能量的64位尾数

异常:

参考性能:

vect_s16_energy

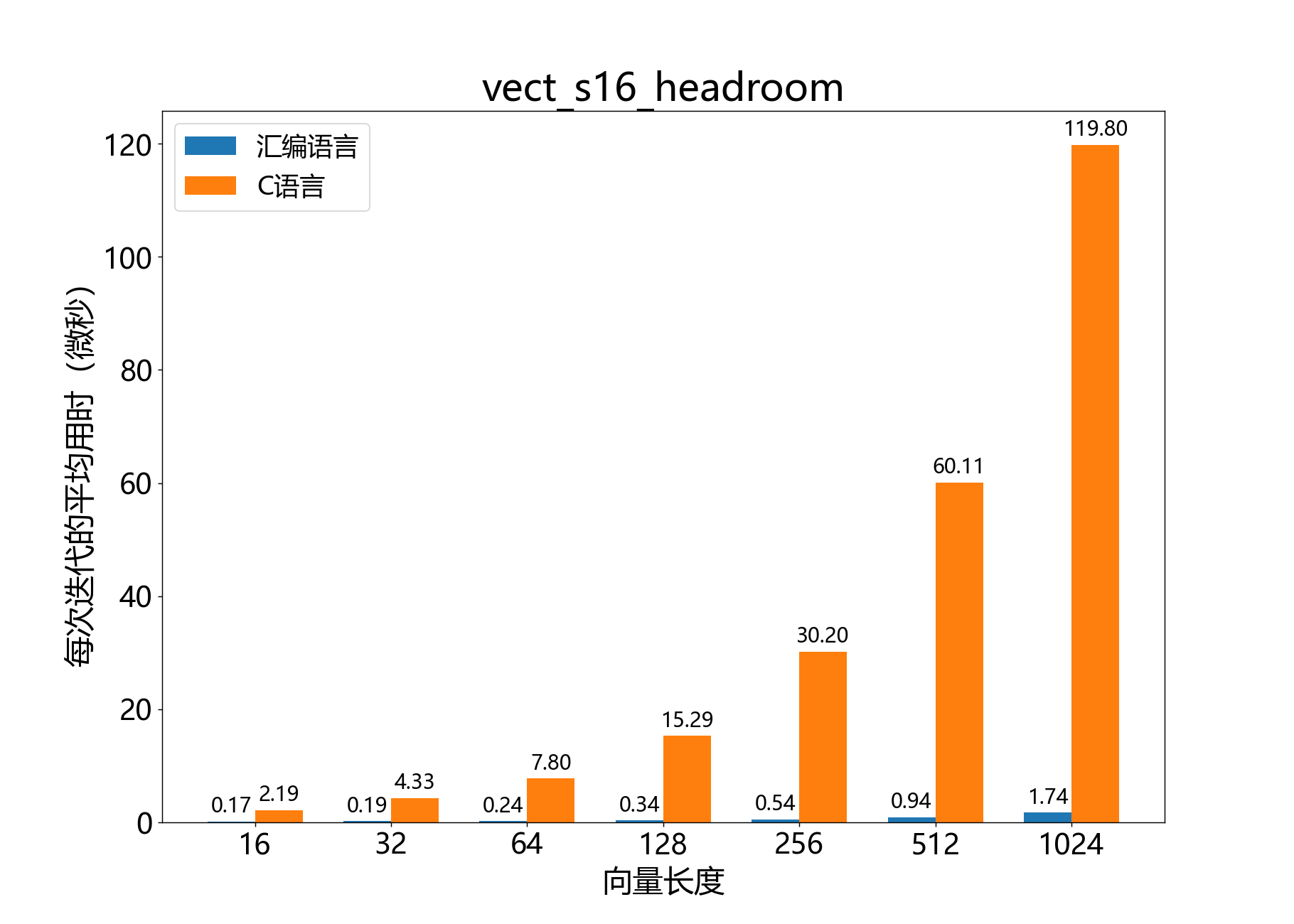
headroom_t vect_s16_headroom()​

计算16位向量的头空间。

N位整数的头空间是该整数的值可以左移的位数，而不会丢失任何信息。等效地，头空间是最前面的符号位数减一。

int16_t数组的头空间是其每个int16_t元素的头空间的最小值。

该函数高效地遍历b[]的元素以确定其头空间。

b[]表示16位向量 bˉ\bar{b}。b[]必须从字对齐的地址开始。

length是b[]中的元素数量。

该函数的操作可以定义为：

a←min ⁣{HR16(x0),HR16(x1),...,HR16(xlength−1)}a \leftarrow min\!\{ HR_{16}\left(x_0\right), HR_{16}\left(x_1\right), ..., HR_{16}\left(x_{length-1}\right) \}

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const unsigned length – [in] 向量 bˉ\bar{b} 中的元素数量

返回值:

  • 向量 bˉ\bar{b} 的头空间

异常:

参见:

  • vect_s32_headroom,
  • vect_complex_s16_headroom,
  • vect_complex_s32_headroom

参考性能:

vect_s16_headroom

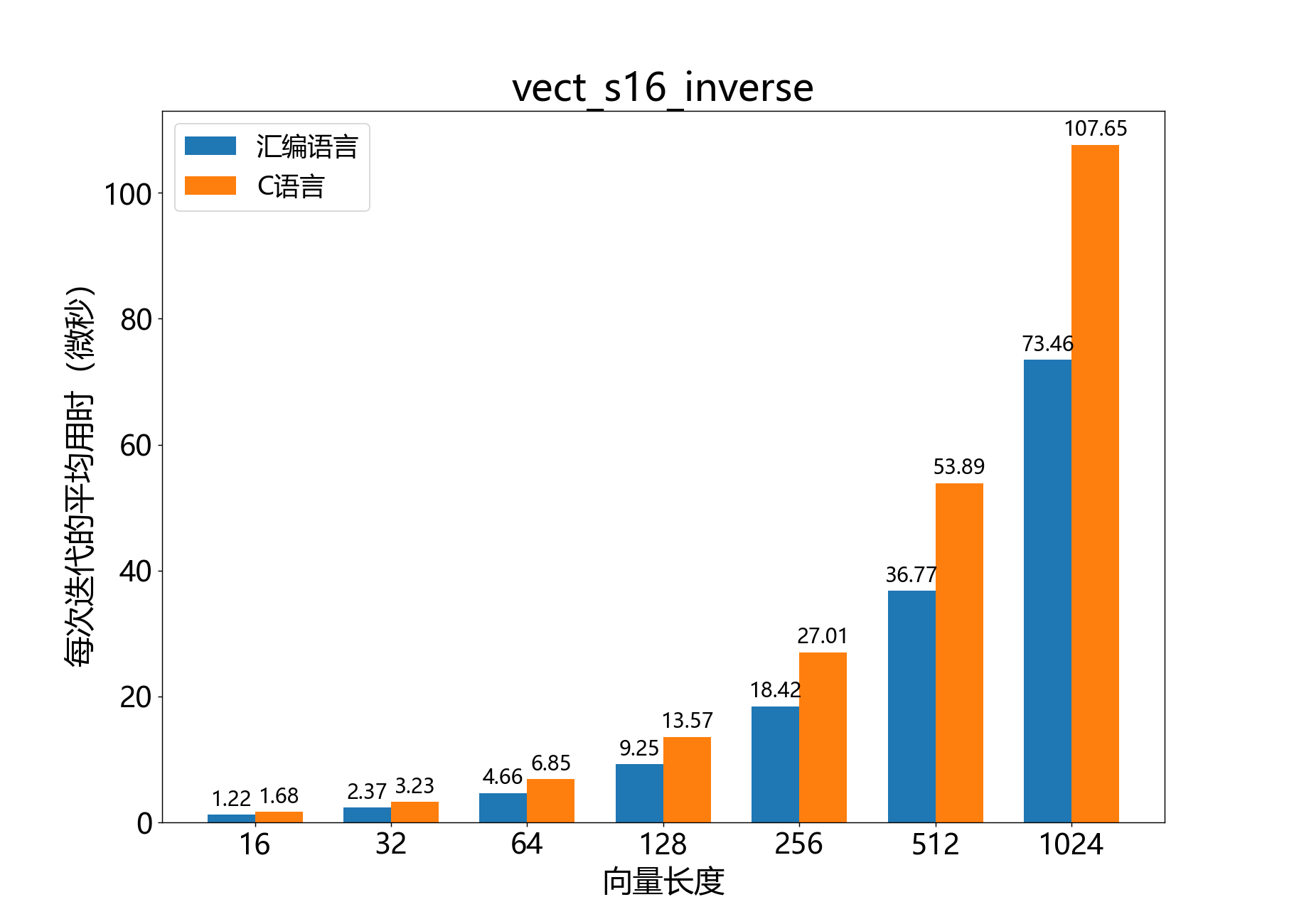
void vect_s16_inverse()​

计算16位向量的倒数。

a[]和b[]分别表示16位尾数向量 aˉ\bar{a} 和 bˉ\bar{b}。该操作可以在b[]上安全地原地执行。

length是每个向量中的元素数量。

scale是一个用于最大化结果精度的缩放参数。

该函数的操作可以定义为：

ak←⌊2scalebk⌋ 其中 k∈0 ... (length−1)a_k \leftarrow \lfloor\frac{2^{scale}}{b_k}\rfloor \quad\text{ 其中 }k\in 0\ ...\ (length-1)

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=scale−b_expa\_exp = scale - b\_exp。

函数vect_s16_inverse_prepare()可用于获取 a_expa\_exp 和 scalescale 的值。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const unsigned length – [in] 向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量

  • const unsigned scale – [in] 计算倒数时应用于被除数的缩放因子

返回值:

  • 输出向量 aˉ\bar{a} 的头空间

参见:

  • vect_s16_inverse_prepare

参考性能:

vect_s16_inverse

int16_t vect_s16_max()​

找出16位向量中的最大值。

b[]表示16位向量 bˉ\bar{b}。它必须从字对齐的地址开始。

length是 bˉ\bar{b} 中的元素数量。

操作:

max{x0,x1,...,xlength−1}max\{ x_0, x_1, ..., x_{length-1} \}

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则返回的值 aa 是浮点值 a⋅2a_expa \cdot 2^{a\_exp} 的16位尾数，其中 a_exp=b_expa\_exp = b\_exp。

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const unsigned length – [in] 向量 bˉ\bar{b} 中的元素数量

返回值:

  • bˉ\bar{b} 中的最大值

异常:

参考性能:

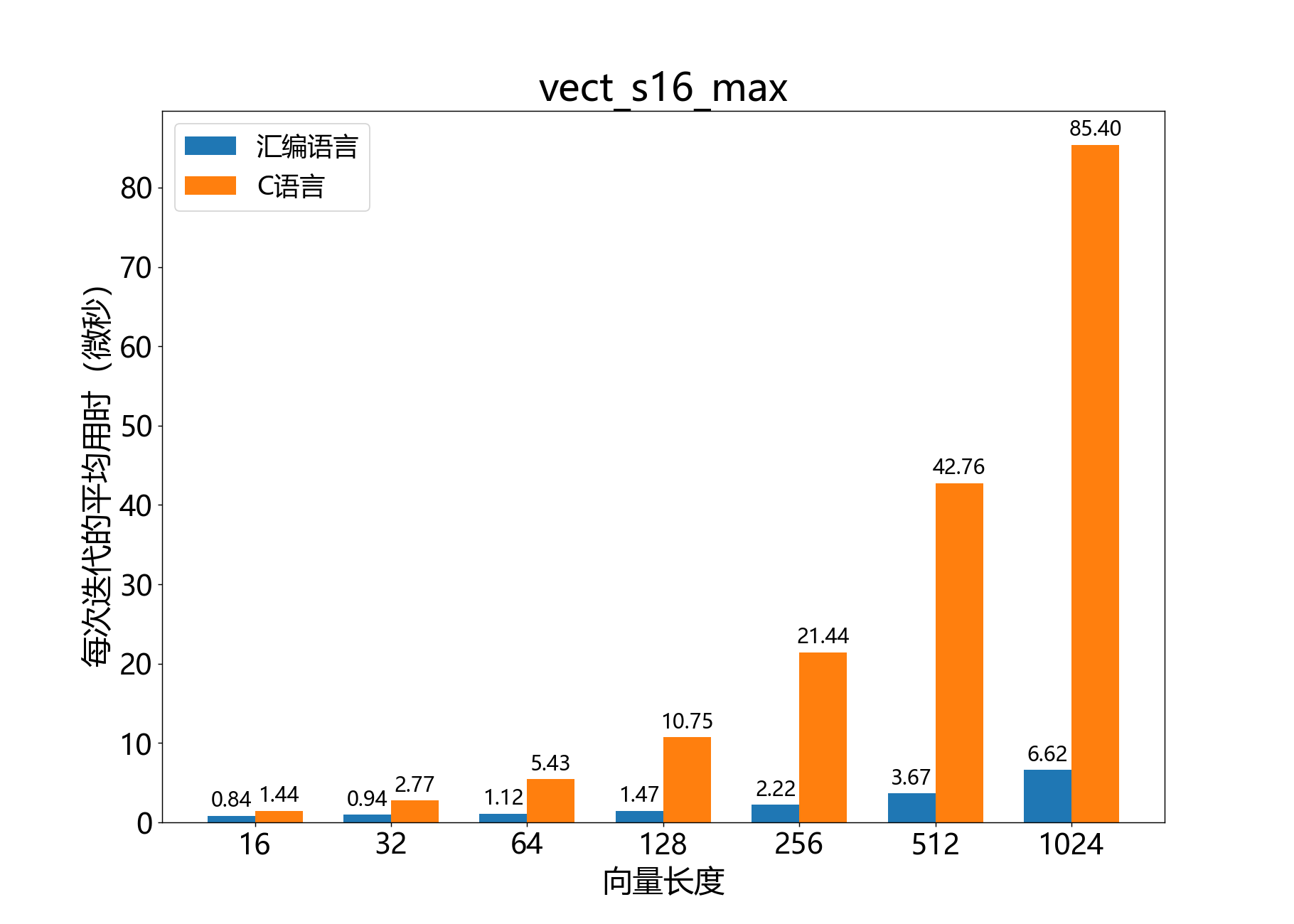
vect_s16_max

headroom_t vect_s16_max_elementwise()​

获取两个16位向量的逐元素最大值。

a[]、b[]和c[]分别表示16位尾数向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c}。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行，但不能在c[]上执行。

length是每个向量中的元素数量。

b_shr和c_shr是应用于 bˉ\bar{b} 和 cˉ\bar{c} 的有符号算术右移量。

操作:

bk′←sat16(⌊bk⋅2−b_shr⌋)ck′←sat16(⌊ck⋅2−c_shr⌋)ak←max(bk′,ck′) 其中 k∈0 ... (length−1)\begin{align*} b_k' & \leftarrow sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ c_k' & \leftarrow sat_{16}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\ a_k & \leftarrow max(b_k', c_k') \\ & \qquad\text{ 其中 }k\in 0\ ...\ (length-1) \end{align*}

块浮点数:

如果 bˉ\bar{b} 和 cˉ\bar{c} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 和 cˉ⋅2c_exp\bar{c} \cdot 2^{c\_exp} 的尾数，则结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_exp+b_shr=c_exp+c_shra\_exp = b\_exp + b\_shr = c\_exp + c\_shr。

可以使用函数 vect_2vec_prepare() 根据输入指数 b_expb\_exp 和 c_expc\_exp 以及输入头空间 b_hrb\_hr 和 c_hrc\_hr 来获取 a_expa\_exp、b_shrb\_shr 和 c_shrc\_shr 的值。

警告:

为了正确运行，此函数要求每个尾数向量 aa 在应用移位后至少有1位头空间。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const int16_t c[] – [in] 输入向量 cˉ\bar{c}
  • const unsigned length – [in] 向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量
  • const right_shift_t b_shr – [in] 应用于 bˉ\bar{b} 的右移量
  • const right_shift_t c_shr – [in] 应用于 cˉ\bar{c} 的右移量

返回值:

  • 向量 aˉ\bar{a} 的头空间

异常:

参考性能:

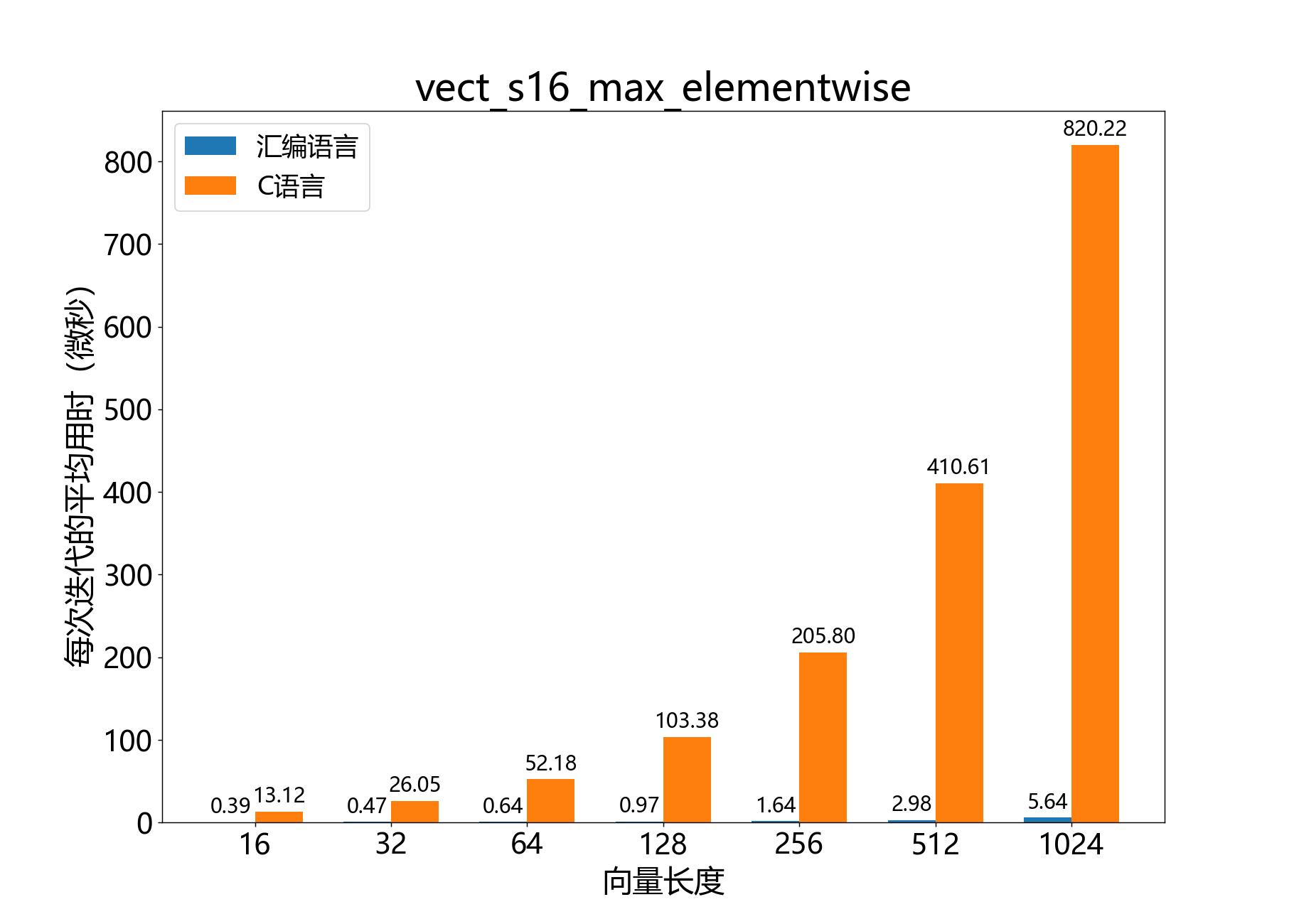
vect_s16_max_elementwise

int16_t vect_s16_min()​

找出16位向量中的最小值。

b[]表示16位向量 bˉ\bar{b}。它必须从字对齐的地址开始。

length是 bˉ\bar{b} 中的元素数量。

操作:

min{x0,x1,...,xlength−1}min\{ x_0, x_1, ..., x_{length-1} \}

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则返回的值 aa 是浮点值 a⋅2a_expa \cdot 2^{a\_exp} 的16位尾数，其中 a_exp=b_expa\_exp = b\_exp。

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const unsigned length – [in] 向量 bˉ\bar{b} 中的元素数量

返回值:

  • bˉ\bar{b} 中的最小值

异常:

参考性能:

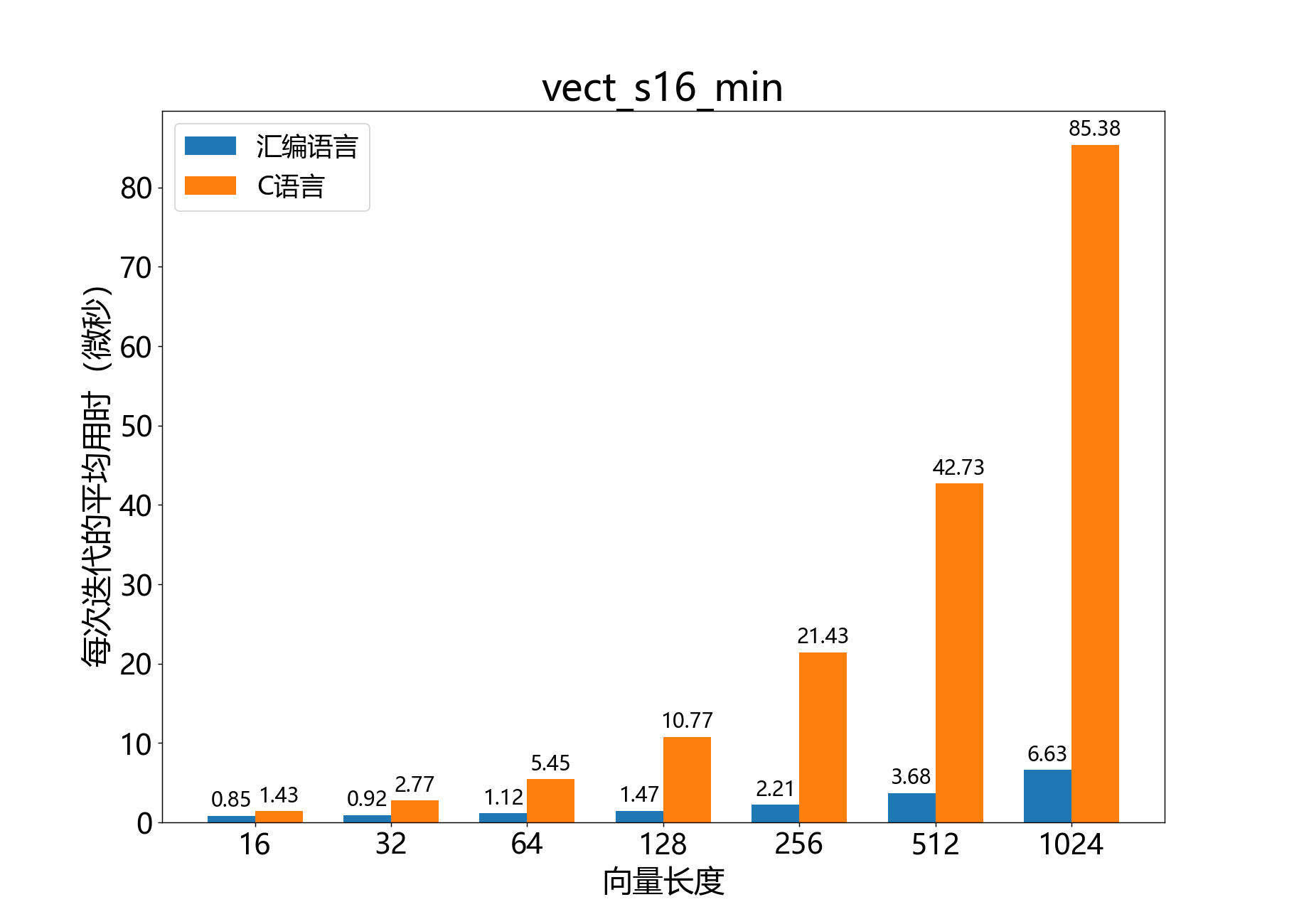
vect_s16_min

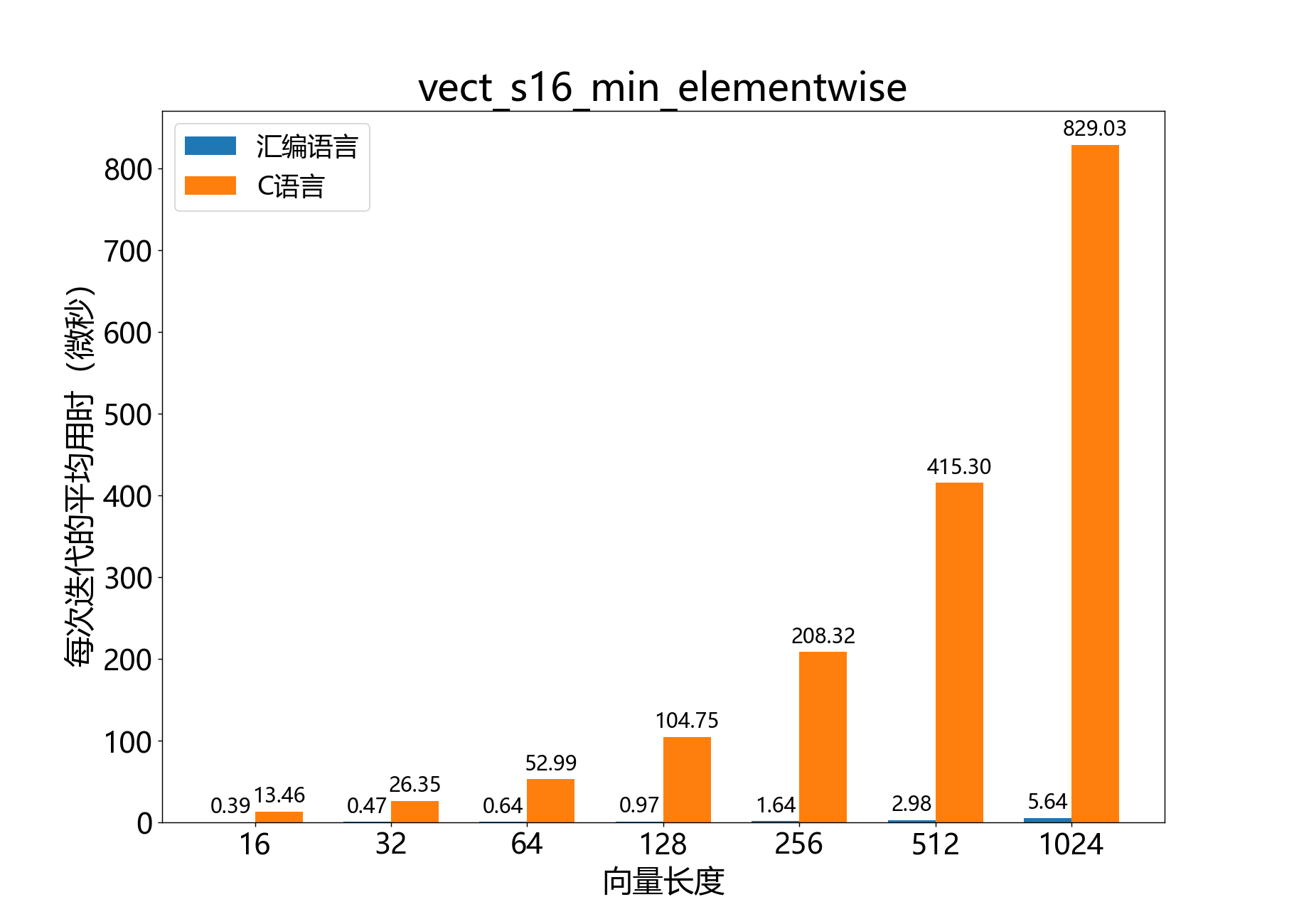
headroom_t vect_s16_min_elementwise()​

获取两个16位向量的逐元素最小值。

a[]、b[]和c[]分别表示16位尾数向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c}。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行，但不能在c[]上执行。

length是每个向量中的元素数量。

b_shr和c_shr是应用于 bˉ\bar{b} 和 cˉ\bar{c} 的有符号算术右移。

操作:

bk′←sat16(⌊bk⋅2−b_shr⌋)ck′←sat16(⌊ck⋅2−c_shr⌋)ak←min(bk′,ck′)其中 k∈0 ... (length−1)\begin{align*} & b_k' \leftarrow sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ & c_k' \leftarrow sat_{16}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\ & a_k \leftarrow min(b_k', c_k') \\ & \qquad\text{其中 }k\in 0\ ...\ (length-1) \end{align*}

块浮点数:

如果 bˉ\bar{b} 和 cˉ\bar{c} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 和 cˉ⋅2c_exp\bar{c} \cdot 2^{c\_exp} 的尾数，则结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_exp+b_shr=c_exp+c_shra\_exp = b\_exp + b\_shr = c\_exp + c\_shr。

函数 vect_2vec_prepare() 可以根据输入指数 b_expb\_exp 和 c_expc\_exp 以及输入头空间 b_hrb\_hr 和 c_hrc\_hr 来获取 a_expa\_exp、b_shrb\_shr 和 c_shrc\_shr 的值。

警告: 为了正确运行，该函数要求每个尾数向量 aˉ\bar{a} 在应用移位后至少有1位头空间。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const int16_t c[] – [in] 输入向量 cˉ\bar{c}
  • const unsigned length – [in] 向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量
  • const right_shift_t b_shr – [in] 应用于 bˉ\bar{b} 的右移量
  • const right_shift_t c_shr – [in] 应用于 cˉ\bar{c} 的右移量

返回值: 向量 aˉ\bar{a} 的头空间

异常: 如果a、b或c不是字对齐的，则引发ET_LOAD_STORE异常（参见 笔记：向量对齐）

参考性能:

vect_s16_min_elementwise

headroom_t vect_s16_macc()​

逐元素将一个16位向量与另一个16位向量相乘，并将结果累加到累加器中。

acc[]表示16位累加器尾数向量 aˉ\bar{a}。每个 aka_k 是 acc[k]。

b[]和c[]分别表示16位输入尾数向量 bˉ\bar{b} 和 cˉ\bar{c}，其中每个 bkb_k 是 b[k]，每个 ckc_k 是 c[k]。

每个输入向量必须从字对齐的地址开始。

length是每个向量中的元素数量。

acc_shr是应用于累加器 aka_k 的有符号算术右移。

bc_sat是应用于 bkb_k 和 ckc_k 的乘积之前的无符号算术右移。

操作:

vk←round(sat16(bk⋅ck⋅2−bc_sat))a^k←sat16(ak⋅2−acc_shr)ak←sat16(a^k+vk)其中 k∈0 ... (length−1)\begin{align*} & v_k \leftarrow round( sat_{16}( b_k \cdot c_k \cdot 2^{-bc\_sat} ) ) \\ & \hat{a}_k \leftarrow sat_{16}( a_k \cdot 2^{-acc\_shr} ) \\ & a_k \leftarrow sat_{16}( \hat{a}_k + v_k ) \\ & \qquad\text{其中 }k\in 0\ ...\ (length-1) \end{align*}

块浮点数:

如果输入 bˉ\bar{b} 和 cˉ\bar{c} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 和 cˉ⋅2c_exp\bar{c} \cdot 2^{c\_exp} 的尾数，并且输入 aˉ\bar{a} 是累加器BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp}，则输出的 aˉ\bar{a} 的指数为 2a_exp+acc_shr2^{a\_exp + acc\_shr}。

为了使累加在数学上有意义，必须选择 bc_satbc\_sat，使得 a_exp+acc_shr=b_exp+c_exp+bc_sata\_exp + acc\_shr = b\_exp + c\_exp + bc\_sat。

函数 vect_complex_s16_macc_prepare() 可以根据输入指数 a_expa\_exp、b_expb\_exp 和 c_expc\_exp 以及输入头空间 a_hra\_hr、b_hrb\_hr 和 c_hrc\_hr 来获取 a_expa\_exp、acc_shracc\_shr 和 bc_satbc\_sat 的值。

参数:

  • int16_t acc[] – [inout] 累加器 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const int16_t c[] – [in] 输入向量 cˉ\bar{c}
  • const unsigned length – [in] 向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量
  • const right_shift_t acc_shr – [in] 应用于累加器元素的有符号右移量
  • const right_shift_t bc_sat – [in] 应用于元素 bkb_k 和 ckc_k 的乘积之前的无符号右移量

返回值: 输出向量 aˉ\bar{a} 的头空间

异常: 如果acc、b或c不是字对齐的，则引发ET_LOAD_STORE异常（参见 笔记：向量对齐）

参见: vect_s16_macc_prepare

参考性能:

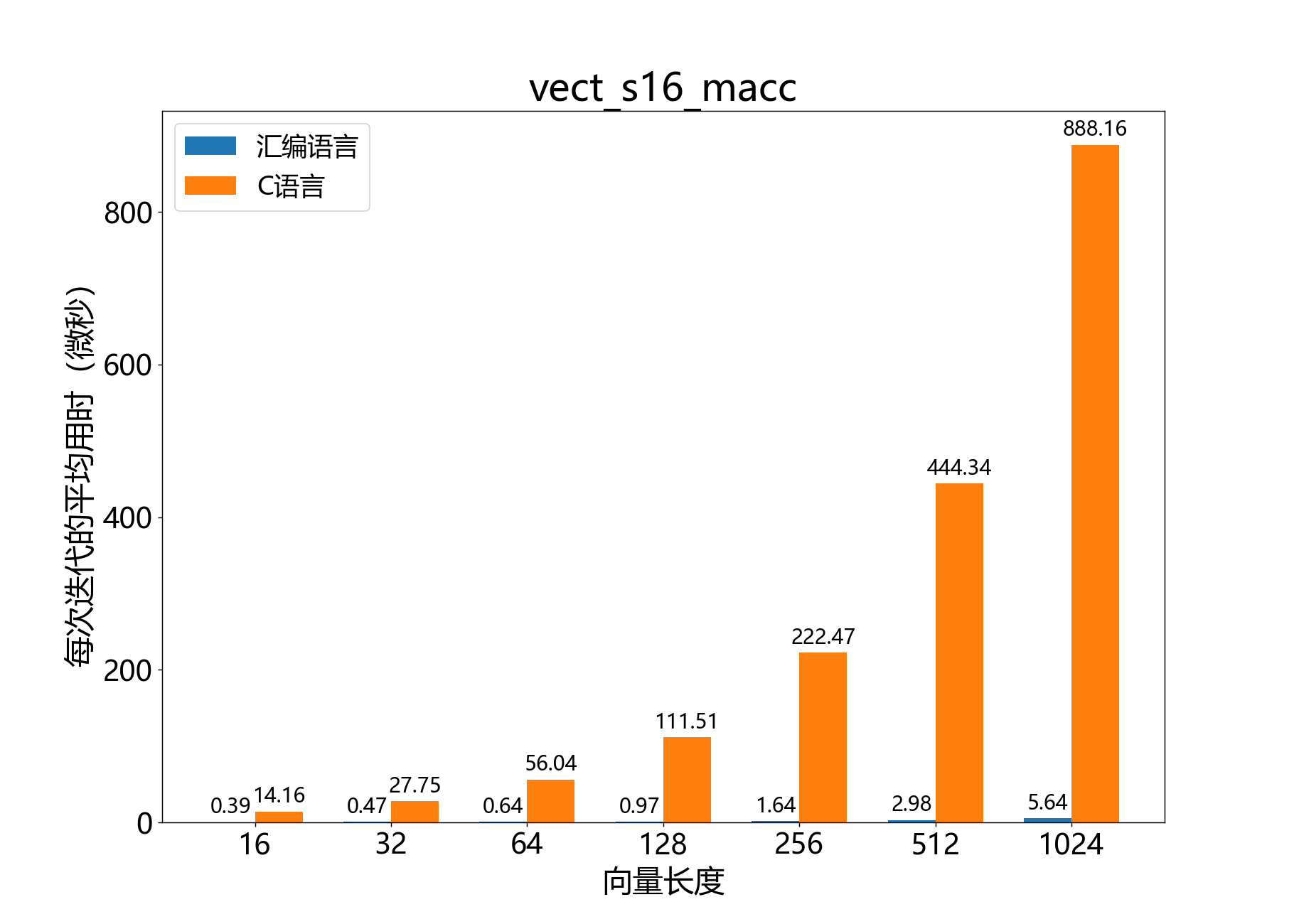
vect_s16_macc

headroom_t vect_s16_nmacc()​

逐元素将一个16位向量与另一个相乘，并从累加器中减去结果。

acc[] 表示16位累加器尾数向量 aˉ\bar{a}。每个 aka_k 是 acc[k]。

b[] 和 c[] 表示16位输入尾数向量 bˉ\bar{b} 和 cˉ\bar{c}，其中每个 bkb_k 是 b[k]，每个 ckc_k 是 c[k]。

每个输入向量必须从字对齐的地址开始。

length 是每个向量中的元素数量。

acc_shr 是应用于累加器元素 aka_k 在累加之前的有符号算术右移量。

bc_sat 是应用于 bkb_k 和 ckc_k 的乘积之后的无符号算术右移量。

操作:

vk←round(sat16(bk⋅ck⋅2−bc_sat))a^k←sat16(ak⋅2−acc_shr)ak←sat16(a^k−vk) 其中 k∈0 ... (length−1)\begin{align*} & v_k \leftarrow \text{round}( sat_{16}( b_k \cdot c_k \cdot 2^{-bc\_sat} ) ) \\ & \hat{a}_k \leftarrow sat_{16}( a_k \cdot 2^{-acc\_shr} ) \\ & a_k \leftarrow sat_{16}( \hat{a}_k - v_k ) \\ & \qquad\text{ 其中 }k\in 0\ ...\ (length-1) \end{align*}

块浮点数:

如果输入 bˉ\bar{b} 和 cˉ\bar{c} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 和 cˉ⋅2c_exp\bar{c} \cdot 2^{c\_exp} 的尾数，并且输入 aˉ\bar{a} 是累加器BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp}，则输出向量 aˉ\bar{a} 的值具有指数 2a_exp+acc_shr2^{a\_exp + acc\_shr}。

为了在数学上使累加有意义，必须选择 bc_satbc\_sat，使得 a_exp+acc_shr=b_exp+c_exp+bc_sata\_exp + acc\_shr = b\_exp + c\_exp + bc\_sat。

函数 vect_complex_s16_nmacc_prepare() 可以根据输入的指数 a_expa\_exp、b_expb\_exp 和 c_expc\_exp 以及输入的头空间 a_hra\_hr、b_hrb\_hr 和 c_hrc\_hr 来获取 a_expa\_exp、acc_shracc\_shr 和 bc_satbc\_sat 的值。

参数:

  • int16_t acc[] – [inout] 累加器 aˉ\bar{a}

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}

  • const int16_t c[] – [in] 输入向量 cˉ\bar{c}

  • const unsigned length – [in] 向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量

  • const right_shift_t acc_shr – [in] 应用于累加器元素的有符号算术右移量

  • const right_shift_t bc_sat – [in] 应用于元素 bkb_k 和 ckc_k 的乘积的无符号算术右移量

返回值:

  • 输出向量 aˉ\bar{a} 的头空间

异常:

  • ET_LOAD_STORE 如果 acc、b 或 c 不是字对齐的，则引发异常（参见 笔记：向量对齐）

另请参阅:

  • vect_s16_nmacc_prepare

参考性能:

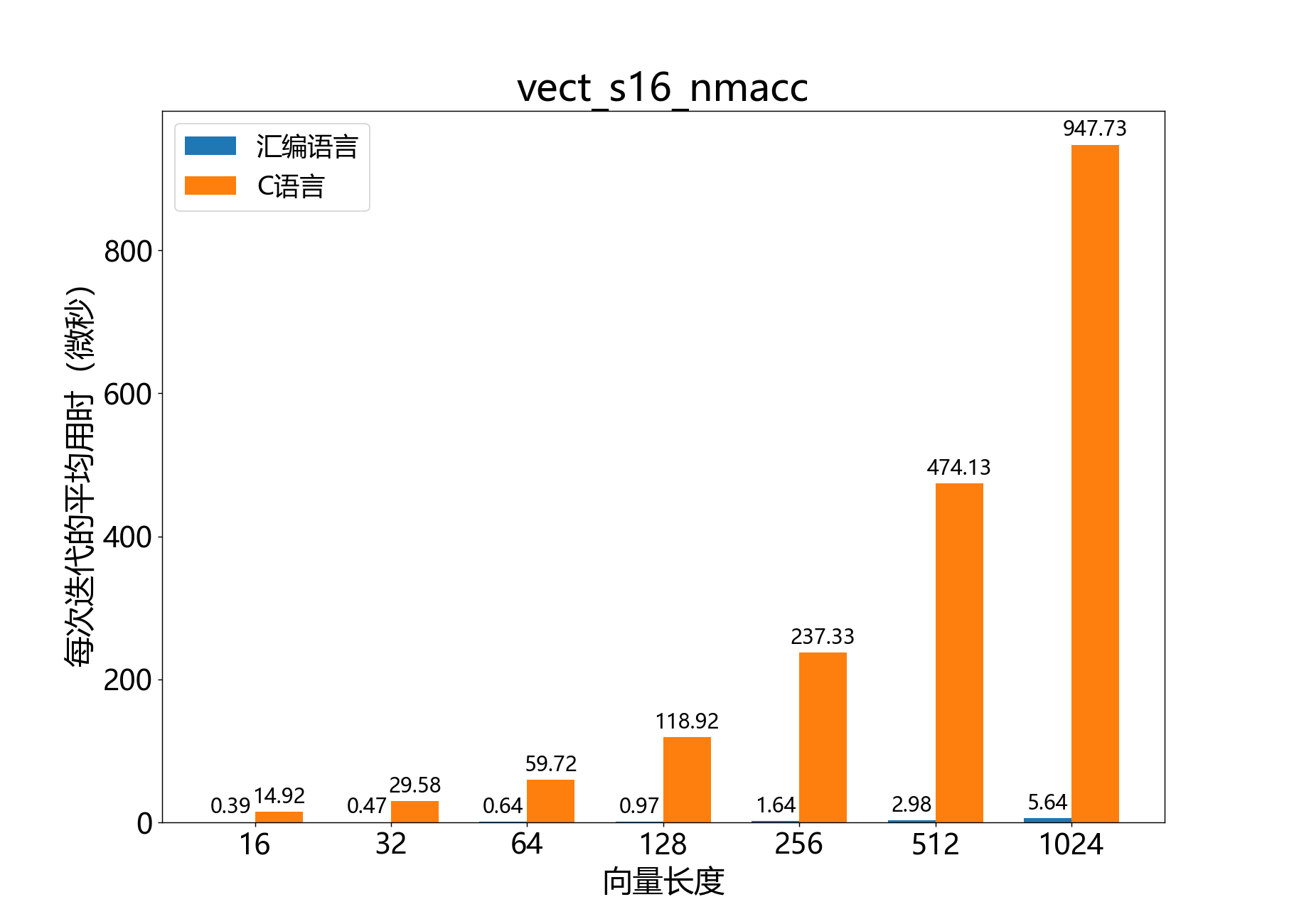
vect_s16_nmacc

headroom_t vect_s16_mul()​

逐元素将两个16位向量相乘。

向量 a[]、b[] 和 c[] 分别表示16位向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c}。每个向量必须从字对齐的地址开始。此操作可以在b[]或c[]上安全地原地执行。

length 是每个向量中的元素数量。

a_shr 是应用于保存次结果的32位累加器的无符号算术右移。

操作:

ak′←bk⋅ckak←sat16(round(ak′⋅2−a_shr)) 其中 k∈0 ... (length−1)\begin{align*} a_k' & \leftarrow b_k \cdot c_k \\ a_k & \leftarrow sat_{16}(round(a_k' \cdot 2^{-a\_shr})) \\ & \qquad\text{ 其中 }k\in 0\ ...\ (length-1) \end{align*}

块浮点数:

如果 bˉ\bar{b} 和 cˉ\bar{c} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 和 cˉ⋅2c_exp\bar{c} \cdot 2^{c\_exp} 的尾数，则结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_exp+c_exp+a_shra\_exp = b\_exp + c\_exp + a\_shr。

函数 vect_s16_mul_prepare() 可以根据输入指数 b_expb\_exp 和 c_expc\_exp 以及输入头空间 b_hrb\_hr 和 c_hrc\_hr 来获取 a_expa\_exp 和 a_shra\_shr 的值。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const int16_t c[] – [in] 输入向量 cˉ\bar{c}
  • const unsigned length – [in] 向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量
  • const right_shift_t a_shr – [in] 应用于32位乘积的右移量

返回值:

  • 输出向量 aˉ\bar{a} 的头空间

异常:

参考性能:

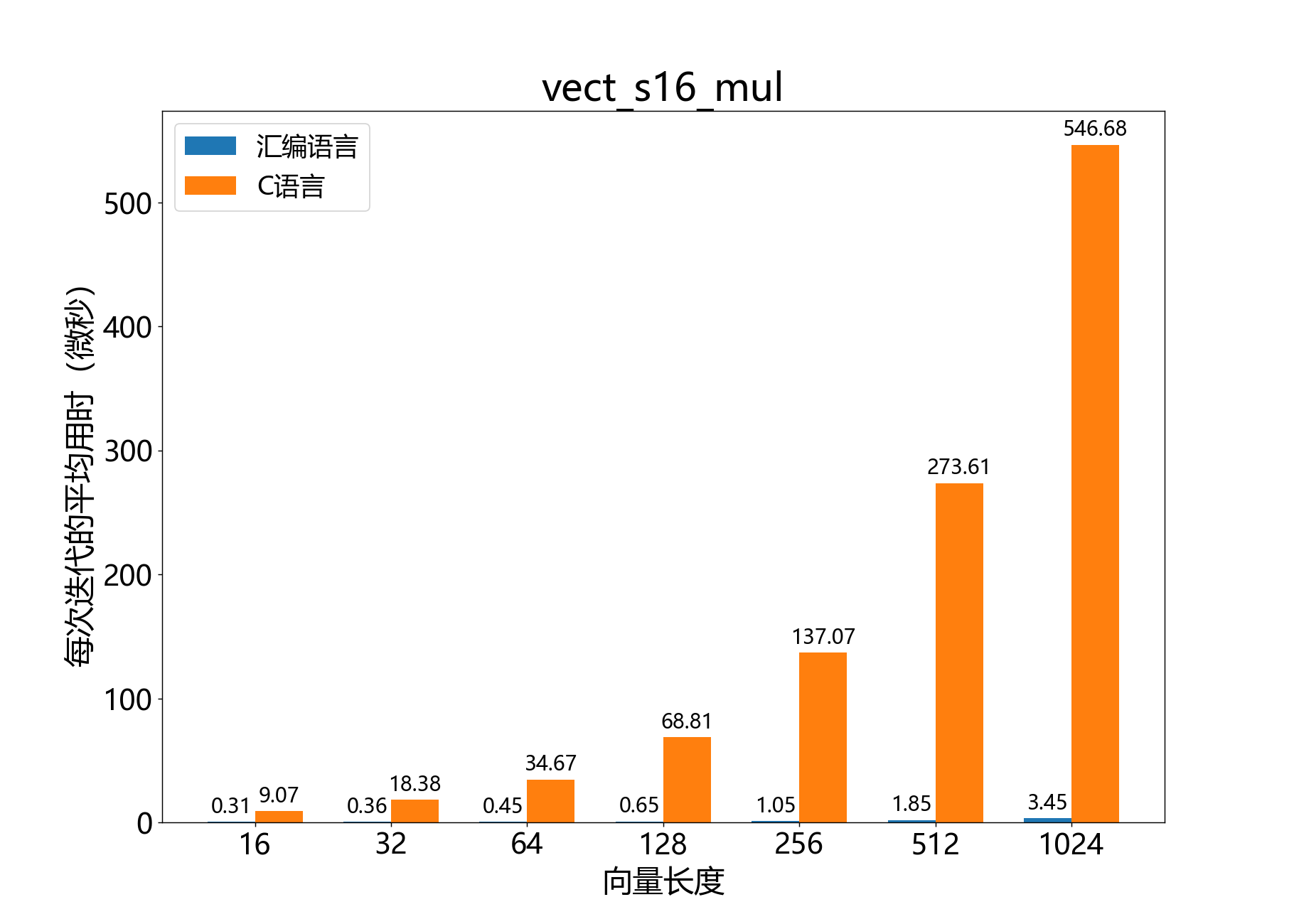
vect_s16_mul

headroom_t vect_s16_rect()​

对16位向量的元素进行修正。

修正确保所有输出都是非负的，将负值更改为0。

a[] 和 b[] 分别表示16位向量 aˉ\bar{a} 和 bˉ\bar{b}。每个向量必须从字对齐的地址开始。此操作可以在b[]上安全地原地执行。

length 是每个向量中的元素数量。

每个输出元素 a[k] 如果为正，则设置为相应输入元素 b[k] 的值，否则将 a[k] 设置为0。

操作:

ak←{bkbk>00bk≤0 其中 k∈0 ... (length−1)a_k \leftarrow \begin{cases} b_k & b_k > 0 \\ 0 & b_k \leq 0\end{cases} \\ \qquad\text{ 其中 }k\in 0\ ...\ (length-1)

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则输出向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_expa\_exp = b\_exp。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const unsigned length – [in] 向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量

返回值:

  • 输出向量 aˉ\bar{a} 的头空间。

异常:

参考性能:

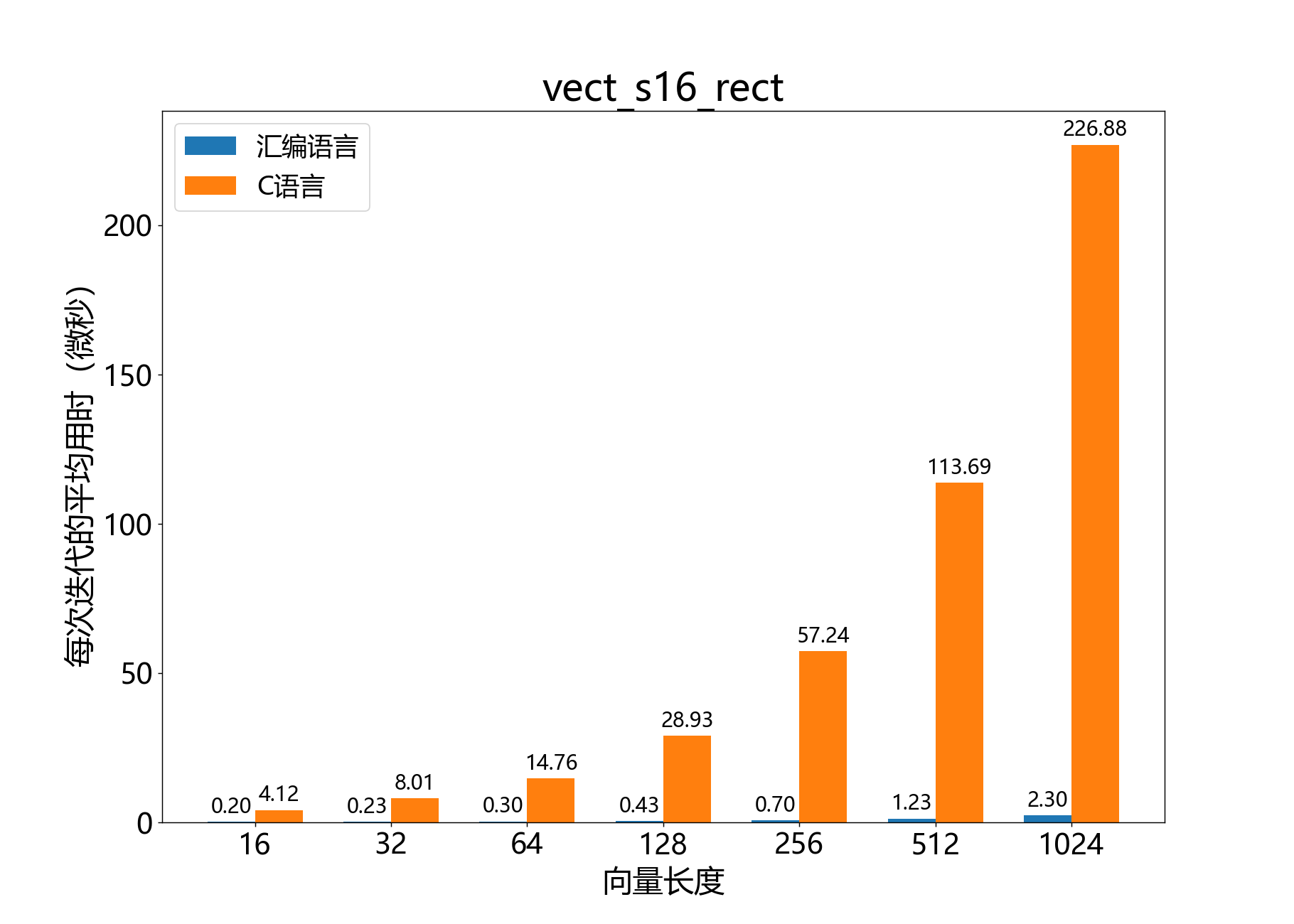
vect_s16_rect

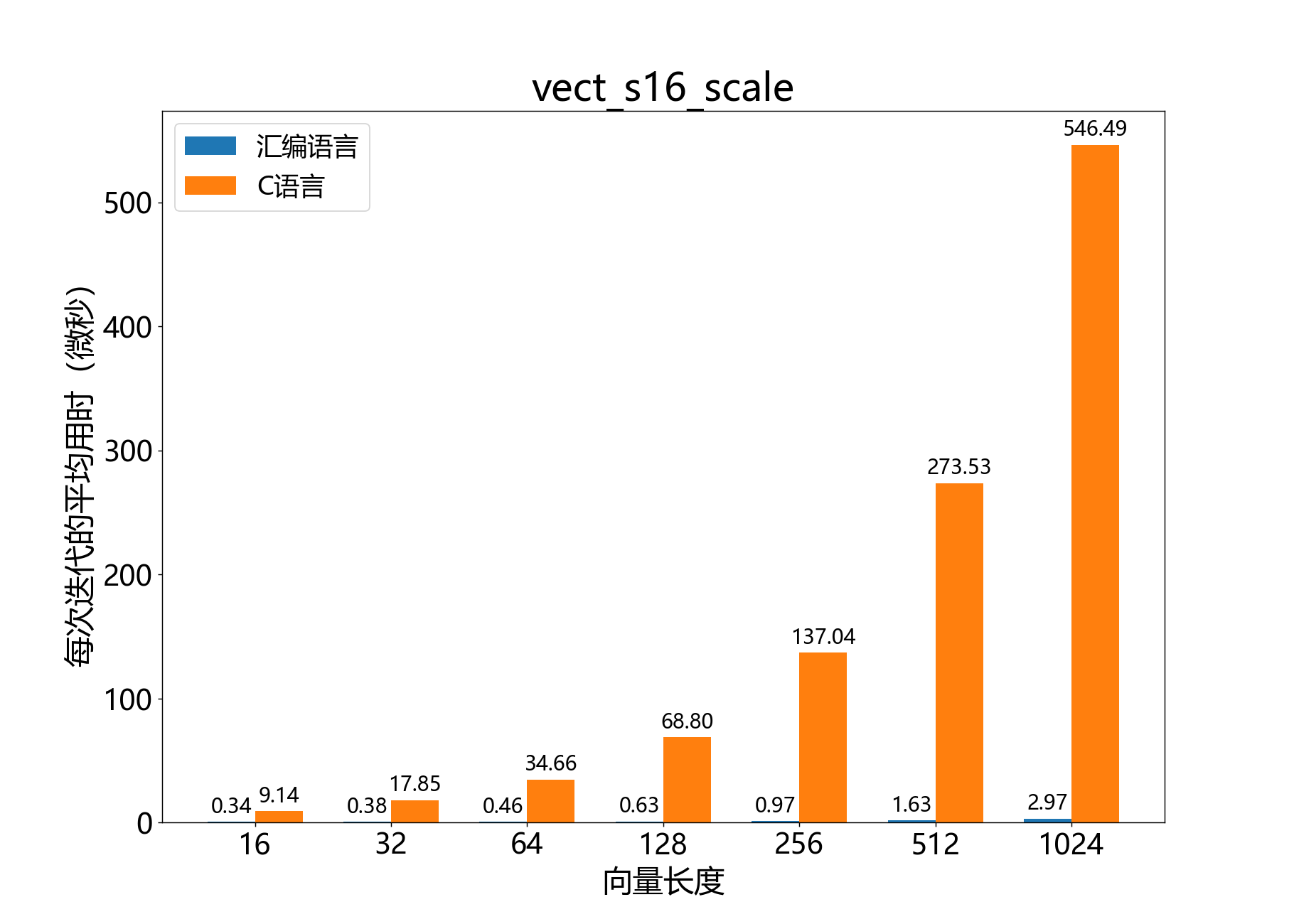
headroom_t vect_s16_scale()​

将一个16位向量乘以一个16位标量。

a[] 和 b[] 分别表示16位向量 aˉ\bar{a} 和 bˉ\bar{b}。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行。

length 是每个向量中的元素数量。

c 是16位标量 cc，用于乘以 bˉ\bar{b} 的元素。

a_shr 是应用于保存次终结果的32位累加器的无符号算术右移。

操作:

ak′←bk⋅cak←sat16(round(ak′⋅2−a_shr))其中k∈0 ... (length−1)\begin{align*} a_k' &\leftarrow b_k \cdot c \\ a_k &\leftarrow sat_{16}(round(a_k' \cdot 2^{-a\_shr}))\\ &其中 k\in 0\ ...\ (length-1) \end{align*}

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，cc 是浮点值 c⋅2c_expc \cdot 2^{c\_exp} 的尾数，则结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_exp+c_exp+a_shra\_exp = b\_exp + c\_exp + a\_shr。

函数 vect_s16_scale_prepare() 可以根据输入指数 b_expb\_exp 和 c_expc\_exp 以及输入头空间 b_hrb\_hr 和 c_hrc\_hr 来获取 a_expa\_exp 和 a_shra\_shr 的值。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const unsigned length – [in] 向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量
  • const int16_t c – [in] 输入标量 cˉ\bar{c}
  • const right_shift_t a_shr – [in] 应用于32位乘积的右移

返回值: 输出向量 aˉ\bar{a} 的头空间

异常: 如果a或b不是字对齐的，则引发ET_LOAD_STORE异常（参见 笔记：向量对齐）

参考性能:

vect_s16_scale

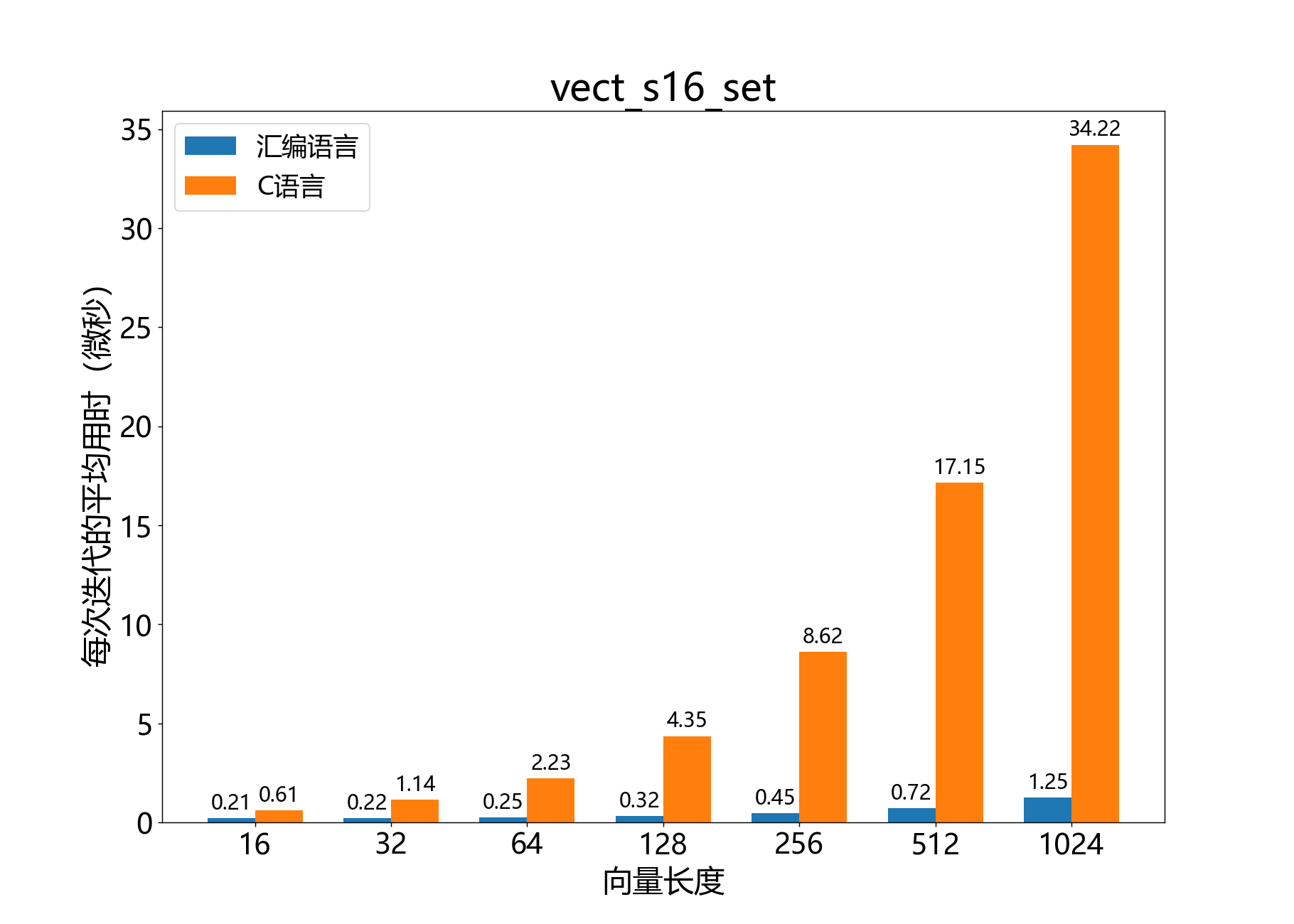
void vect_s16_set()​

将16位向量的所有元素设置为指定的值。

a[] 表示16位向量 aˉ\bar{a}。它必须从字对齐的地址开始。

b 是 aˉ\bar{a} 的元素设置的值。

length 是 a[] 中的元素数量。

操作:

ak←b其中k∈0 ... (length−1)a_k \leftarrow b\\ 其中 k\in 0\ ...\ (length-1)

块浮点数:

如果 bb 是浮点值 b⋅2b_expb \cdot 2^{b\_exp} 的尾数，则输出向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 a_exp=b_expa\_exp = b\_exp。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b – [in] 输入值 bb
  • const unsigned length – [in] 向量 aˉ\bar{a} 中的元素数量

异常: 如果a不是字对齐的，则引发ET_LOAD_STORE异常（参见 笔记：向量对齐）

参考性能:

vect_s16_set

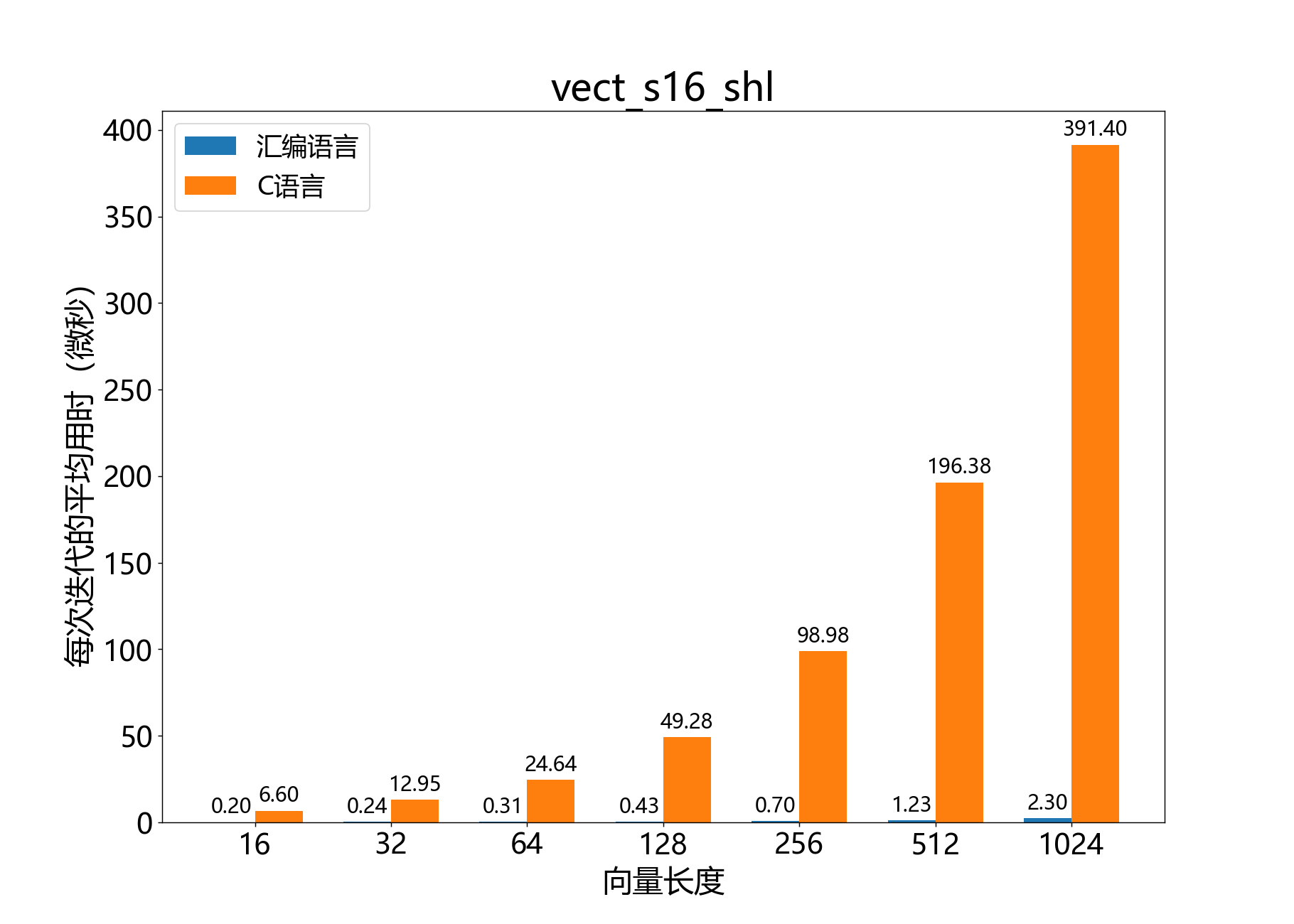
headroom_t vect_s16_shl()​

将16位向量的元素左移指定的位数。

a[]和b[]分别表示16位向量 aˉ\bar{a} 和 bˉ\bar{b}。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行。

length是向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量。

b_shl是应用于 bˉ\bar{b} 的有符号算术左移。

操作:

ak←sat16(⌊bk⋅2b_shl⌋)其中k∈0…(length−1)a_k \leftarrow sat_{16}(\lfloor b_k \cdot 2^{b\_shl} \rfloor) \quad \text{其中} \quad k \in 0 \ldots (length-1)

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数，其中 aˉ=bˉ⋅2b_shl\bar{a} = \bar{b} \cdot 2^{b\_shl} 且 a_exp=b_expa\_exp = b\_exp。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const unsigned length – [in] 向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量
  • const left_shift_t b_shl – [in] 应用于 bˉ\bar{b} 的算术左移

返回值:

  • 输出向量 aˉ\bar{a} 的头空间

异常:

参考性能:

vect_s16_shl

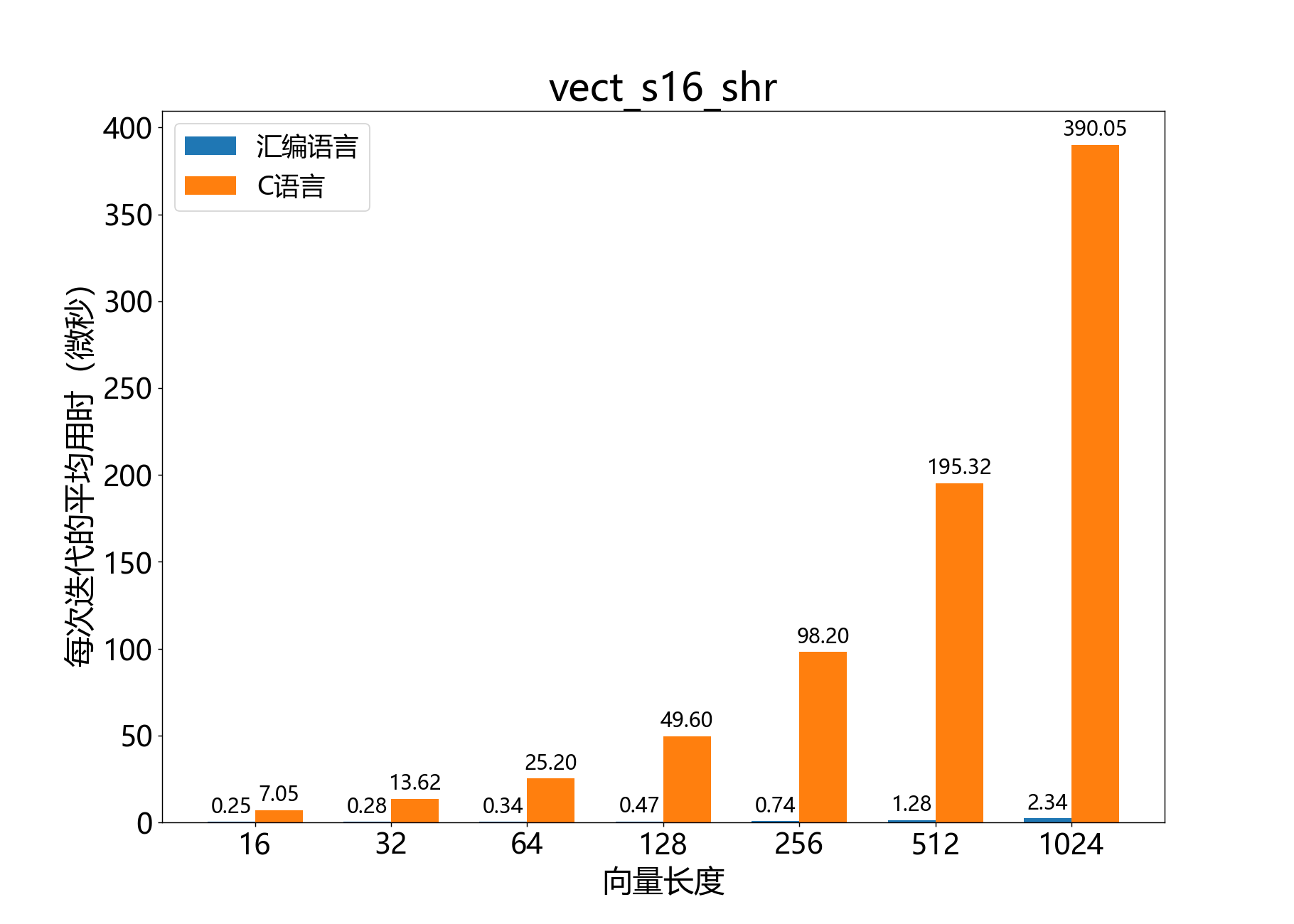
headroom_t vect_s16_shr()​

将16位向量的元素右移指定的位数。

a[]和b[]分别表示16位向量 aˉ\bar a 和 bˉ\bar b。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行。

length是向量 aˉ\bar a 和 bˉ\bar b 中的元素数量。

b_shr是应用于 bˉ\bar b 的有符号算术右移。

操作:

ak←sat16(⌊bk⋅2−b_shr⌋) 其中 k∈0 ... (length−1)a_k \leftarrow sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \quad \text{ 其中 }k\in 0\ ...\ (length-1)

块浮点数:

如果 bˉ\bar b 是BFP向量 bˉ⋅2b_exp\bar b \cdot 2^{b\_exp} 的尾数，则结果向量 aˉ\bar a 是BFP向量 aˉ⋅2a_exp\bar a \cdot 2^{a\_exp} 的尾数，其中 aˉ=bˉ⋅2−b_shr\bar a = \bar b \cdot 2^{-b\_shr}，a_exp=b_expa\_exp = b\_exp。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar a
  • const int16_t b[] – [in] 输入向量 bˉ\bar b
  • const unsigned length – [in] 向量 aˉ\bar a 和 bˉ\bar b 的元素数量
  • const right_shift_t b_shr – [in] 应用于 bˉ\bar b 的右移量

返回值:

  • headroom_t - 输出向量 aˉ\bar a 的头空间

异常:

  • ET_LOAD_STORE - 如果a或b不是字对齐的，则引发异常

参考性能:

vect_s16_shr

headroom_t vect_s16_sqrt()​

计算16位向量的平方根。

a[]和b[]分别表示16位向量 aˉ\bar a 和 bˉ\bar b。每个向量必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行。

length是向量 aˉ\bar a 和 bˉ\bar b 中的元素数量。

b_shr是应用于 bˉ\bar b 的有符号算术右移。

depth是要计算的每个 aka_k 的最高有效位数。例如，depth值为8将仅计算结果的8个最高有效字节，其余字节为0。该参数的最大值为VECT_SQRT_S16_MAX_DEPTH（31）。此操作的时间成本大致与计算的位数成正比。

操作:

bk′←sat16(⌊bk⋅2−b_shr⌋)ak←{bk′if bk′≥00otherwise 其中 k∈0 ... (length−1)其中⋅计算平方根的最高有效depth位。\begin{aligned} b_k' & \leftarrow sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ a_k & \leftarrow \begin{cases} \sqrt{ b_k' } & \text{if } b_k' \geq 0 \\ 0 & \text{otherwise} \end{cases} \\ & \quad \text{ 其中 }k\in 0\ ...\ (length-1) \\ & \quad \text{其中} \sqrt{\cdot} \text{计算平方根的最高有效} depth \text{位。} \end{aligned}

块浮点数:

如果 bˉ\bar b 是BFP向量 bˉ⋅2b_exp\bar b \cdot 2^{b\_exp} 的尾数，则结果向量 aˉ\bar a 是BFP向量 aˉ⋅2a_exp\bar a \cdot 2^{a\_exp} 的尾数，其中 a_exp=(b_exp+b_shr−14)/2a\_exp = (b\_exp + b\_shr - 14)/2。

请注意，由于指数必须是整数，因此 b_exp+b_shrb\_exp + b\_shr 必须是偶数。

函数vect_s16_sqrt_prepare()可以根据输入指数 b_expb\_exp 和头空间 b_hrb\_hr 来获取 a_expa\_exp 和 b_shrb\_shr 的值。

注意:

  • 此函数假设根是实数。负输入元素将导致相应的输出为0。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar a
  • const int16_t b[] – [in] 输入向量 bˉ\bar b
  • const unsigned length – [in] 向量 aˉ\bar a 和 bˉ\bar b 的元素数量
  • const right_shift_t b_shr – [in] 应用于 bˉ\bar b 的右移量
  • const unsigned depth – [in] 要计算的每个输出值的位数

返回值:

  • headroom_t - 输出向量 aˉ\bar a 的头空间

异常:

  • ET_LOAD_STORE - 如果a或b不是字对齐的，则引发异常

参考性能:

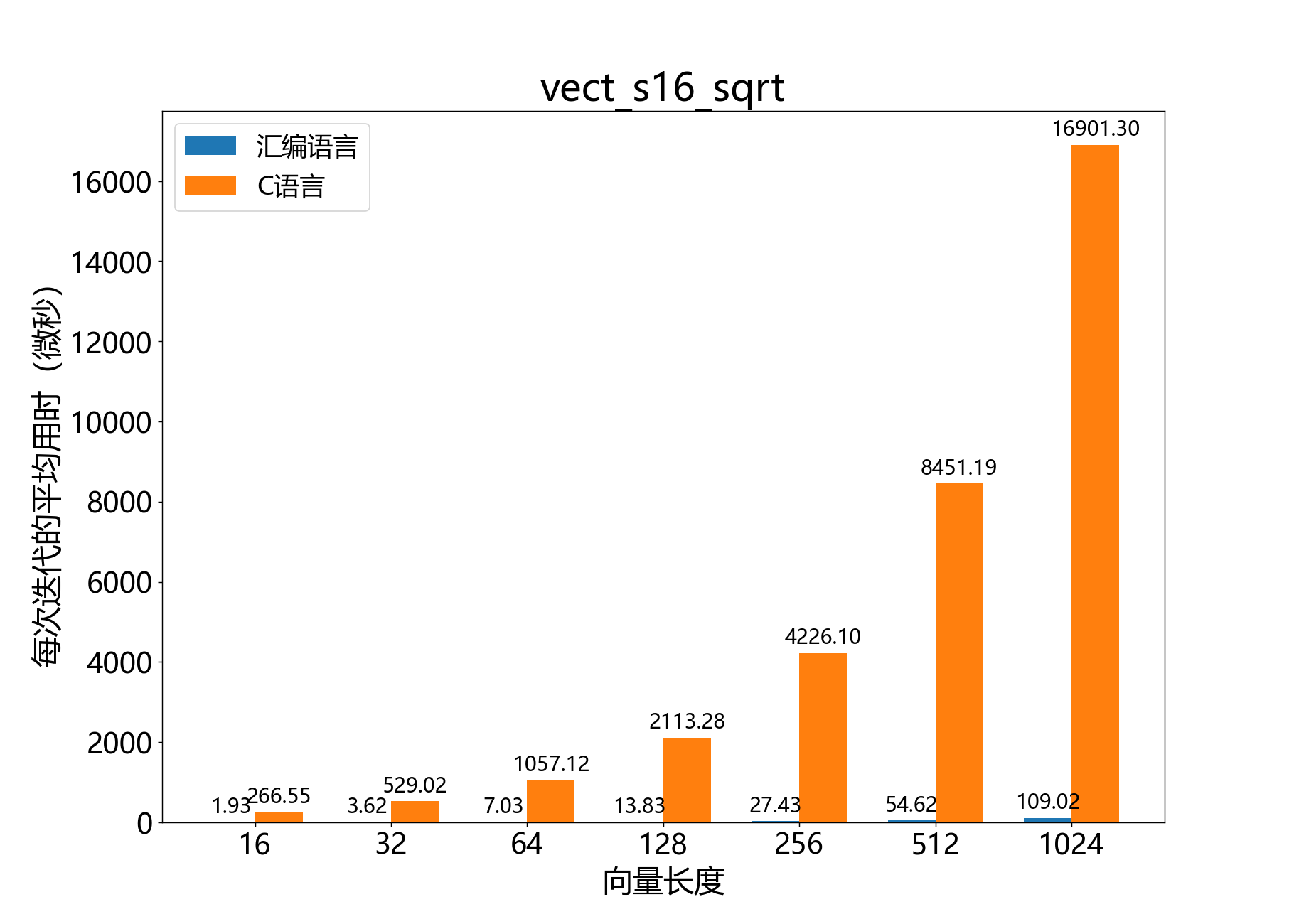
vect_s16_sqrt

headroom_t vect_s16_sub()​

从一个16位BFP向量中减去另一个16位BFP向量。

a[]、b[]和c[]分别表示16位向量 aˉ\bar{a}、bˉ\bar{b}和cˉ\bar{c}。每个向量必须从字对齐的地址开始。可以在b[]或c[]上安全地原地执行此操作。

length是每个向量中的元素数量。

b_shr和c_shr是应用于 bˉ\bar{b} 和 cˉ\bar{c} 的带符号算术右移。

操作:

bk′=sat16(⌊bk⋅2−b_shr⌋)ck′=sat16(⌊ck⋅2−c_shr⌋)ak←sat16 ⁣(bk′−ck′) 其中 k∈0 ... (length−1)\begin{split}\begin{align*} & b_k' = sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ & c_k' = sat_{16}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\ & a_k \leftarrow sat_{16}\!\left( b_k' - c_k' \right) \\ & \qquad\text{ 其中 }k\in 0\ ...\ (length-1) && \end{align*}\end{split}

块浮点数:

如果 bˉ\bar{b} 和 cˉ\bar{c} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 和 cˉ⋅2c_exp\bar{c} \cdot 2^{c\_exp} 的尾数，那么结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的尾数。

在这种情况下，必须选择 b_shrb\_shr 和 c_shrc\_shr 使得 a_exp=b_exp+b_shr=c_exp+c_shra\_exp = b\_exp + b\_shr = c\_exp + c\_shr。只有当幅度与相同指数相关联时，加法或减法才有意义。

函数 vect_s16_sub_prepare() 可用于根据输入指数 b_expb\_exp 和 c_expc\_exp 以及输入头空间 b_hrb\_hr 和 c_hrc\_hr 来获取 a_expa\_exp、b_shrb\_shr 和 c_shrc\_shr 的值。

参数:

  • int16_t a[] – [out] 输出向量 aˉ\bar{a}
  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const int16_t c[] – [in] 输入向量 cˉ\bar{c}
  • const unsigned length – [in] 向量 aˉ\bar{a}、bˉ\bar{b} 和 cˉ\bar{c} 中的元素数量
  • const right_shift_t b_shr – [in] 应用于 bˉ\bar{b} 的右移
  • const right_shift_t c_shr – [in] 应用于 cˉ\bar{c} 的右移

返回值: 输出向量 aˉ\bar{a} 的头空间。

异常: 如果a、b或c不是字对齐的，则引发ET_LOAD_STORE异常（参见 笔记：向量对齐）

参考性能:

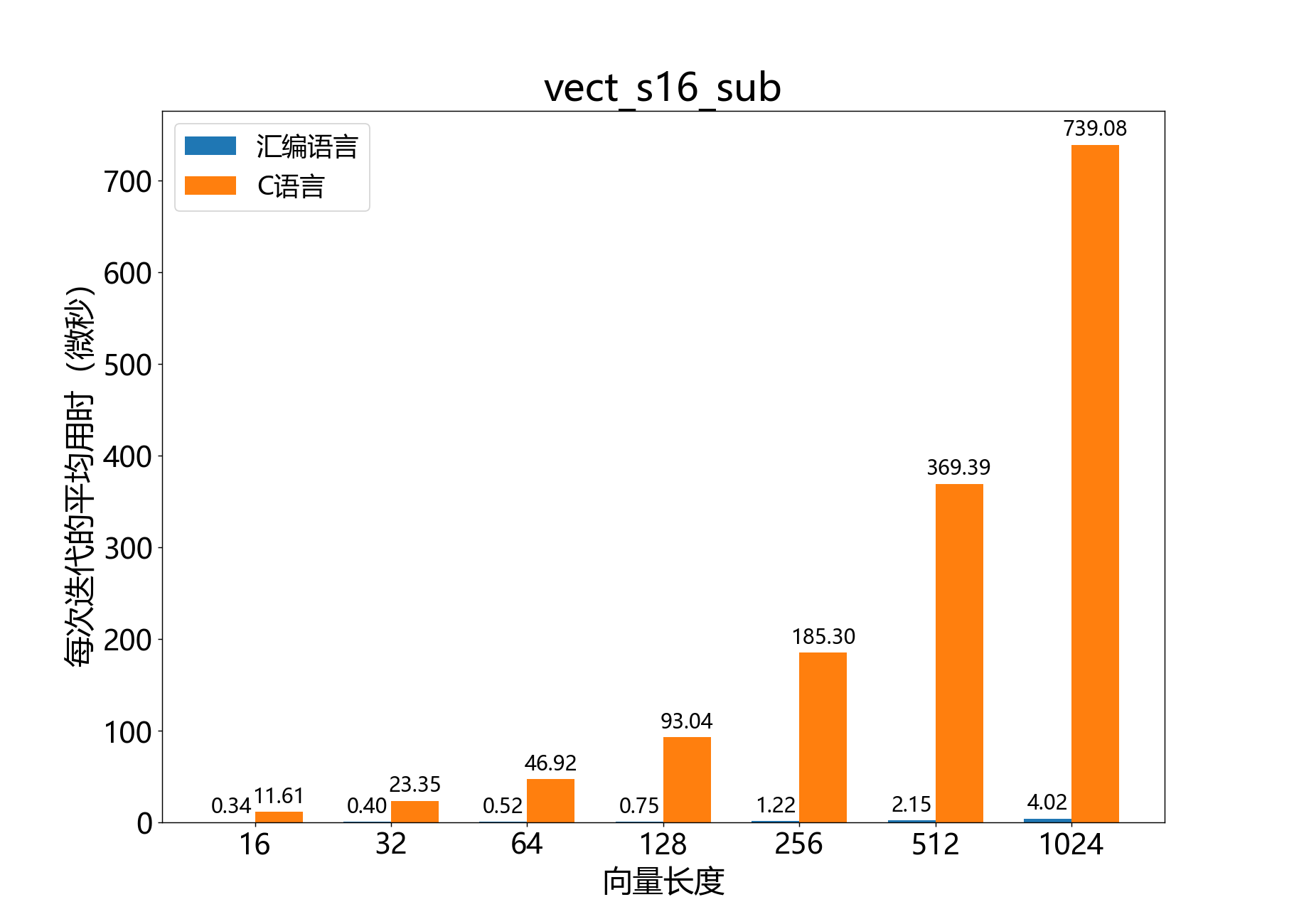
vect_s16_sub

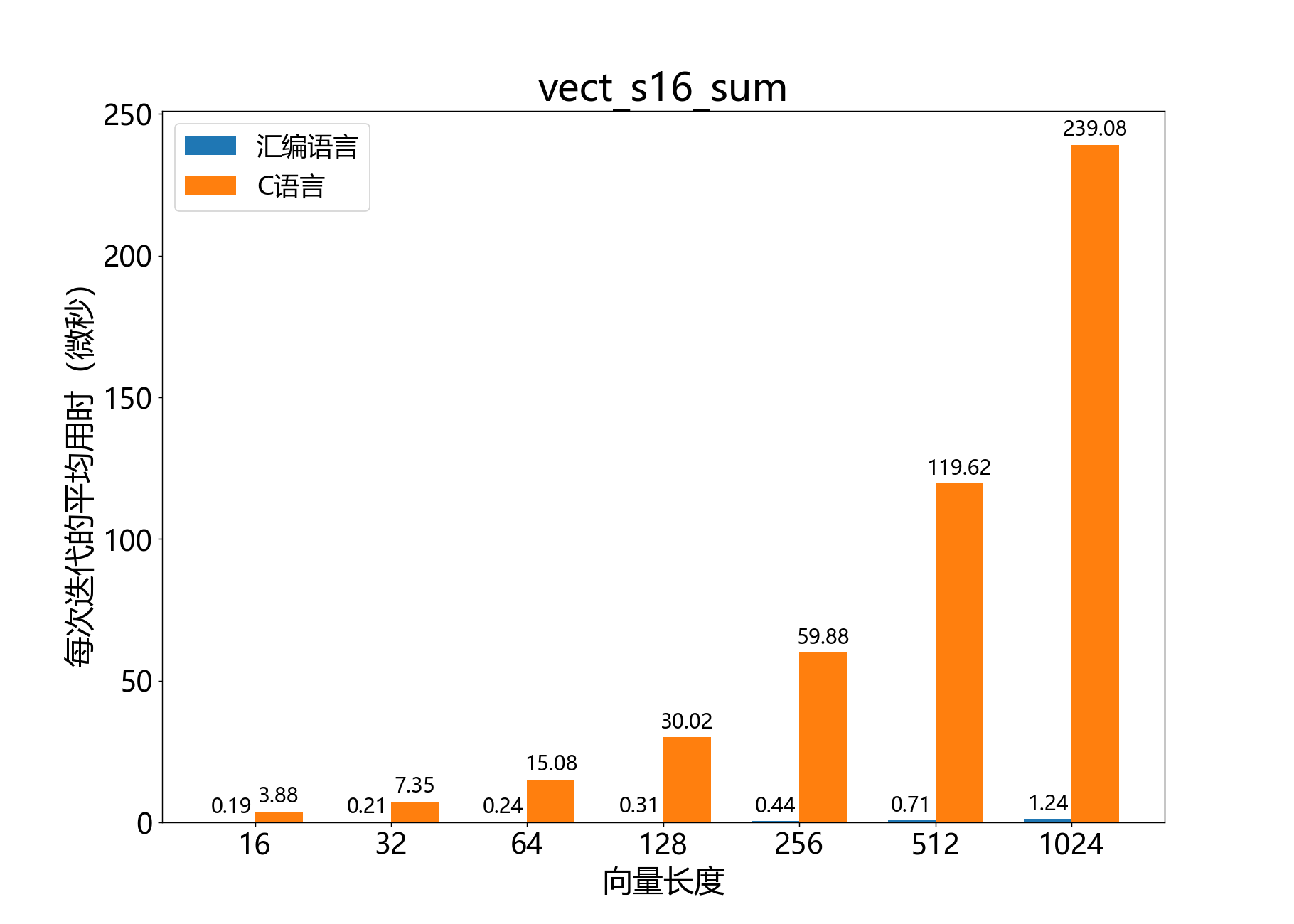
int32_t vect_s16_sum()​

计算16位向量的元素总和。

b[] 表示16位向量 bˉ\bar{b}。b[] 必须从字对齐的地址开始。

length 是 bˉ\bar{b} 中的元素数量。

操作:

a←∑k=0length−1bka \leftarrow \sum_{k=0}^{length-1} b_k

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则返回值 aa 是浮点数 a⋅2a_expa \cdot 2^{a\_exp} 的32位尾数，其中 a_exp=b_expa\_exp = b\_exp。

参数:

  • const int16_t b[] – [in] 输入向量 bˉ\bar{b}
  • const unsigned length – [in] 向量 bˉ\bar{b} 中的元素数量

返回值: 32位总和 aa

异常: 如果b不是字对齐的，则引发ET_LOAD_STORE异常（参见 笔记：向量对齐）

参考性能:

vect_s16_sum

#define VPU_INT16_CTRL_INIT 0x0100​

VPU控制寄存器的初始化值。

在使用chunk_s16_accumulate()函数时，应将vpu_ctrl初始化为此值。

将VPU控制寄存器设置为此值将使其处于16位模式，并清除头空间寄存器。

#define VPU_INT16_HEADROOM_FROM_CTRL(X) ((15)-(X & 0x1F))​

从VPU控制寄存器的值中推导出16位头空间。

与chunk_s16_accumulate()结合使用，用于计算最终的头空间。

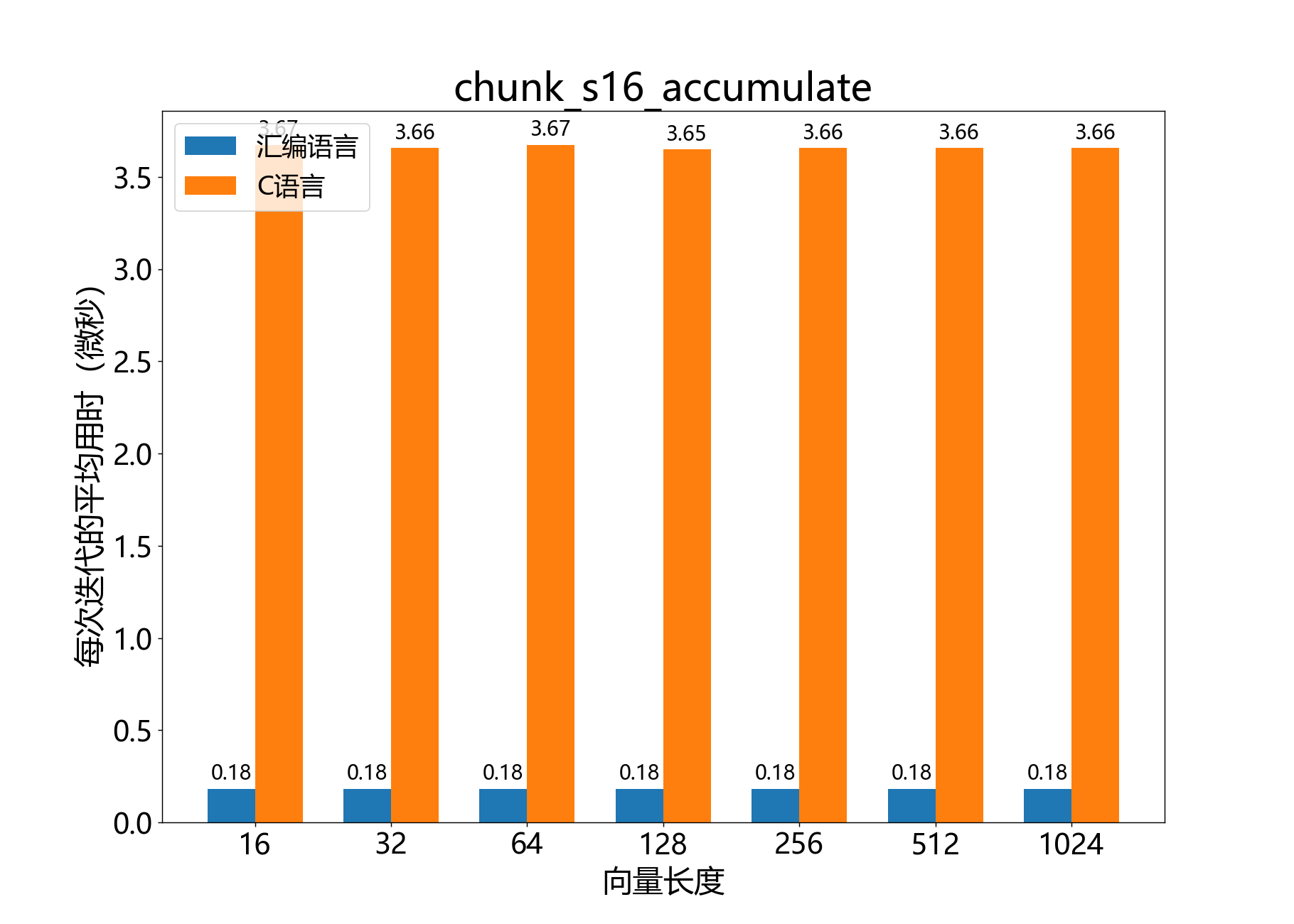
unsigned chunk_s16_accumulate()​

将一个16位向量块累加到一个32位累加器块中。

该函数将16位向量块 bˉ\bar{b} 移位并累加到32位累加器向量块 aˉ\bar{a} (acc) 中。它用于高效地累加多个（可能是许多）16位向量。

累加器向量 aˉ\bar{a} 将其元素存储在两个16位向量块中，对应于累加器在VPU寄存器 vD 和 vR 中的内部存储方式。有关累加器结构的详细信息，请参见 split_acc_s32_t。

在将 bˉ\bar{b} 累加到 aˉ\bar{a} 之前，对 bˉ\bar{b} 进行了带符号算术右移 b_shr。当 bˉ\bar{b} 和 aˉ\bar{a} 是块浮点向量的尾数时，使用 b_shr 允许这些向量具有不同的指数。当需要定期调用此函数且每个 bˉ\bar{b} 可能具有不同的指数时，这也很重要。

b_shr 必须满足条件 -14 <= b_shr <= 14，否则此函数的行为未定义。

该操作定义为：

ak←ak+floor(bk2−b_shr)a_k \leftarrow a_k + floor( \frac{b_k}{2^{-\mathtt{b\_shr}}} )

参数:

  • split_acc_s32_t* acc – [inout] 要累加到的累加器向量 aˉ\bar{a}

  • const int16_t b[VPU_INT16_EPV] – [in] 要累加的16位向量块 bˉ\bar{b}

  • const right_shift_t b_shr – [in] 要应用于 bˉ\bar{b} 的右移量

  • const unsigned vpu_ctrl – [in] 当前 VPU 控制寄存器的状态

返回值:

  • 当前 VPU 控制寄存器的状态。

异常:

VPU 控制值:

输入的 vpu_ctrl 跟踪累加过程中 VPU 的控制寄存器状态。它用于特定地跟踪累加器向量 Aˉ\bar A 的头空间。

在开始一系列累加调用时，传入的值应初始化为 VPU_INT16_CTRL_INIT。此函数在完成后返回更新后的 VPU 控制寄存器状态，下一次累加调用时应将其作为 vpu_ctrl 传入。

其目的是每次只处理一个“块”（在16位模式下，一个16元素块）的调用。但是，调用者通常希望知道整个向量的头空间，该向量可能由许多这样的块组成。因此，vpu_ctrl 是一个持续通过每个调用跟踪整个向量的值。

在累加所有块之后，可以使用 VPU_INT16_HEADROOM_FROM_CTRL() 宏获取累加器向量的头空间。注意，这将产生最大值为 15。

累加多个值:

如果将许多向量块 Bˉ\bar B 累加到相同的累加器中（当使用块浮点时，如果与 Aˉ\bar A 关联的指数明显大于与 Bˉ\bar B 关联的指数，则可能只有少数累加），可能会发生饱和。

当可能发生饱和时，用户必须监视 Aˉ\bar A 的头空间（使用返回的值和 VPU_INT16_HEADROOM_FROM_CTRL()）以检测是否没有进一步的头空间。只要至少有 1 位头空间，调用此函数就不会饱和。

通常，在使用块浮点时，会执行以下操作：

  1. 使用 vect_s32_merge_accs() 将 Aˉ\bar A 转换为标准的 int32_t 向量
  2. 使用 vect_s32_shr() 对 Aˉ\bar A 的值进行右移
  3. 将与 Aˉ\bar A 关联的指数按相同的右移量递增
  4. 使用 vect_s32_split_accs() 将 Aˉ\bar A 再次转换为分割累加器格式

在累加时，将 b_shr 设置为 Bˉ\bar B 关联的指数减去 Aˉ\bar A 关联的指数，将自动调整为 Aˉ\bar A 的新指数。

参见:

  • split_acc_s32_t
  • VPU_INT16_CTRL_INIT
  • VPU_INT16_HEADROOM_FROM_CTRL()
  • vect_s32_merge_accs()
  • vect_s32_shr()
  • vect_s32_split_accs()

参考性能:

chunk_s16_accumulate

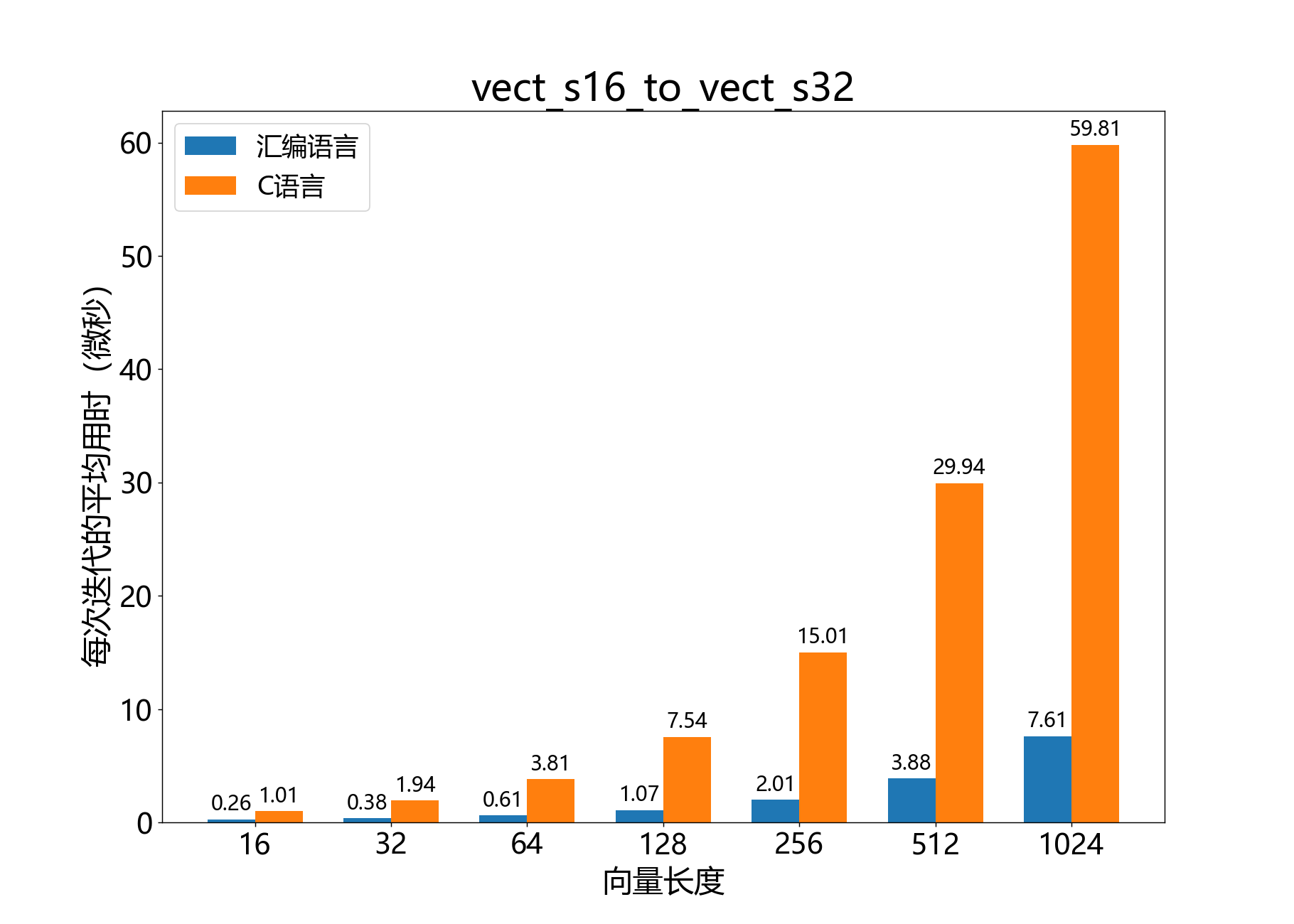
void vect_s16_to_vect_s32()​

将16位向量转换为32位向量。

a[]表示32位输出向量 aˉ\bar{a}。

b[]表示16位输入向量 bˉ\bar{b}。

每个向量必须从字对齐的地址开始。

length是每个向量中的元素数量。

该操作可以表示为：

ak←bk⋅28 其中 k∈0 ... (length−1)\begin{split}\begin{align*} & a_k \leftarrow b_k \cdot 2^{8} \\ & \qquad\text{ 其中 }k\in 0\ ...\ (length-1) && \end{align*}\end{split}

块浮点数:

如果 bˉ\bar{b} 是BFP向量 bˉ⋅2b_exp\bar{b} \cdot 2^{b\_exp} 的尾数，则结果向量 aˉ\bar{a} 是BFP向量 aˉ⋅2a_exp\bar{a} \cdot 2^{a\_exp} 的32位尾数。如果 a_exp=b_exp−8a\_exp = b\_exp - 8，则该操作实际上没有改变所表示的值。

注意事项:

  • 乘以 282^8 是VPU行为的产物。事实证明，包含 282^8 的因子更加高效。如果不需要这个因子，可以使用 vect_s32_shr() 函数，并将 b_shr 的值设置为 8，以在之后去除缩放。
  • 此函数不返回输出向量 aˉ\bar{a} 的头空间。输出的头空间始终比输入的头空间大8位。

参数:

  • int32_t a[] – [out] 32位输出向量 aˉ\bar{a}

  • const int16_t b[] – [in] 16位输入向量 bˉ\bar{b}

  • const unsigned length – [in] 向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量

异常:

参考性能:

vect_s16_to_vect_s32

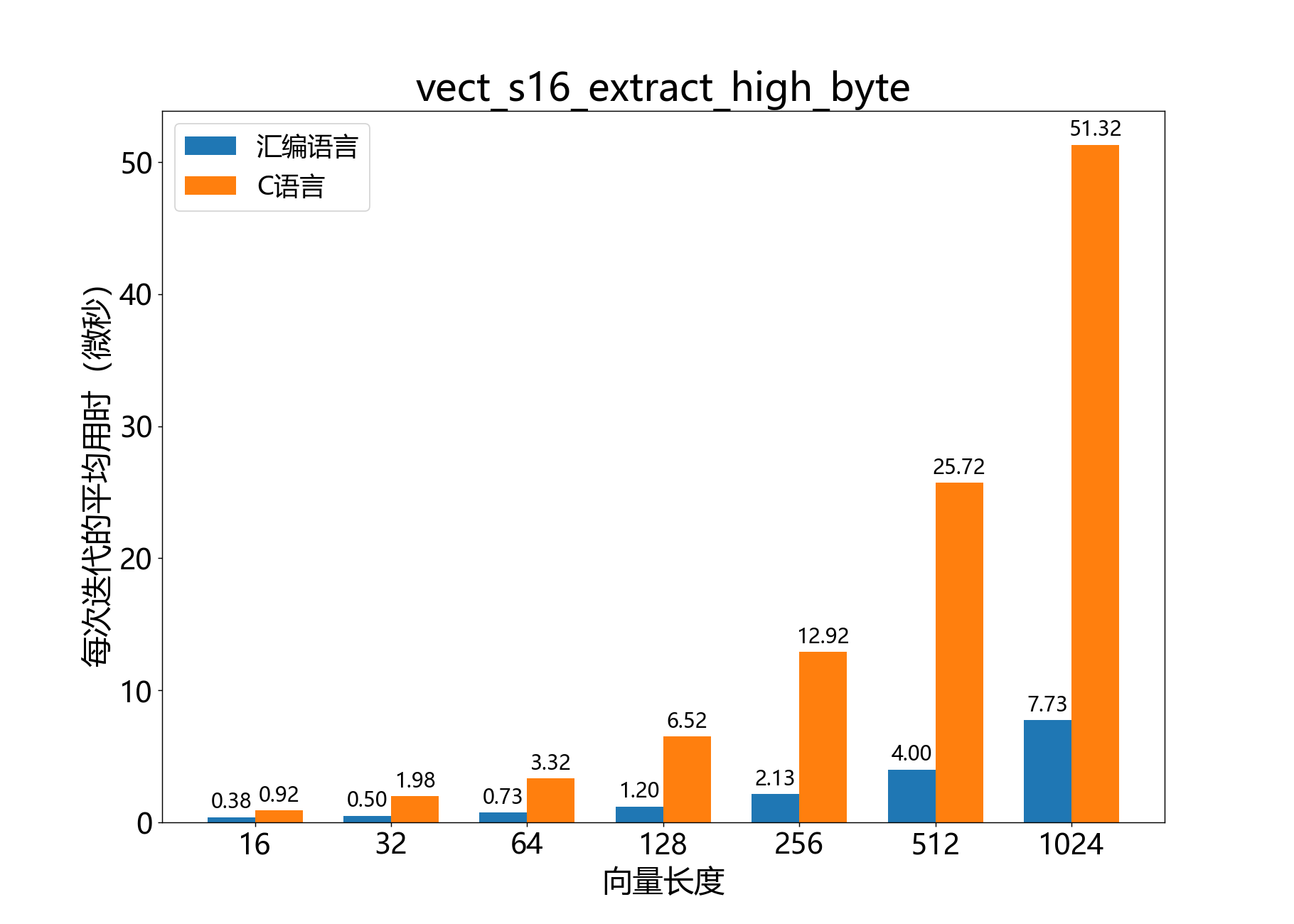
void vect_s16_extract_high_byte()​

提取包含16位向量的最高字节的8位向量。

这是一个实用函数，例如，在优化混合宽度乘积时使用。它提取每个元素的最高字节（不进行舍入或饱和），并将其插入输出向量。

参数:

  • int8_t a[] – [out] 8位输出向量 aˉ\bar{a}

  • const int16_t b[] – [in] 16位输入向量 bˉ\bar{b}

  • const unsigned len – [in] 向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量

异常:

参见:

参考性能:

vect_s16_extract_high_byte

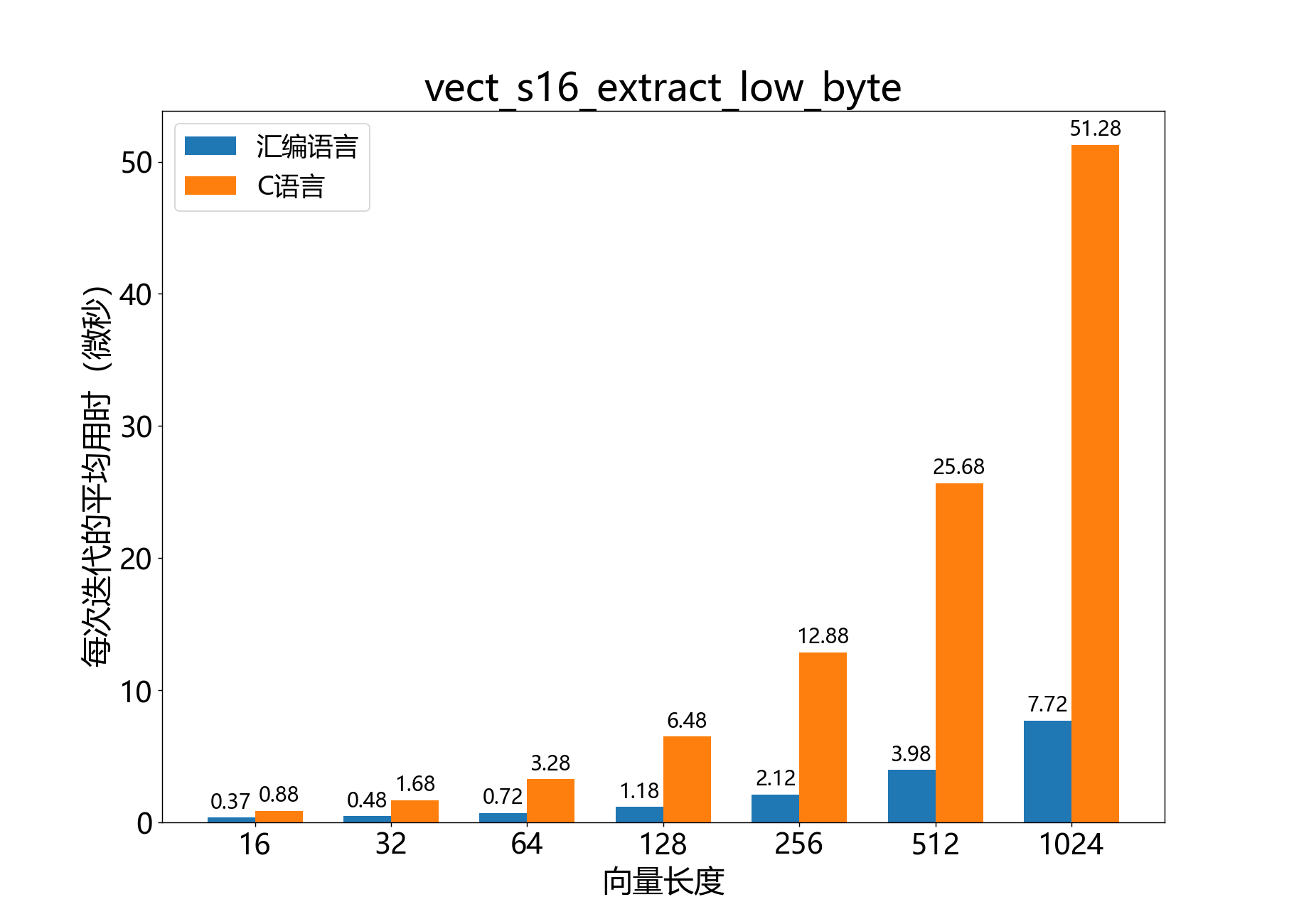
void vect_s16_extract_low_byte()​

提取包含16位向量的最低字节的8位向量。

这是一个实用函数，例如，在优化混合宽度乘积时使用。它提取每个元素的最低字节（不进行舍入或饱和），并将其插入输出向量。

参数:

  • int8_t a[] – [out] 8位输出向量 aˉ\bar{a}

  • const int16_t b[] – [in] 16位输入向量 bˉ\bar{b}

  • const unsigned len – [in] 向量 aˉ\bar{a} 和 bˉ\bar{b} 中的元素数量

异常:

参见:

参考性能:

vect_s16_extract_low_byte

编辑此页
本文最后由 Vergil Wong 更新于