Skip to main content
欢迎来到PAWPAW技术文档网站，了解更多信息。

第2A部分：转向定点实现

在第2A部分中，我们放弃了浮点运算，转而使用定点运算。第2A部分与第1B部分一样，使用纯C语言实现了内积。与第1B部分一样，这不是一个高度优化的实现（与第1C部分相比）。优化将在下一个阶段进行。

最终，我们会发现纯C语言编写的定点实现比第1C部分中的优化浮点实现要慢。

实现​

src/part2A/part2A.c
/**
 * 这是硬件线程的入口点，实际上将应用FIR滤波器。
 * 
 * `c_audio` 是与 tile[0] 交换 PCM 音频数据的通道。
 */
void filter_task(
    chanend_t c_audio)
{
  // 用于存储输入样本历史记录的缓冲区
  q1_31 sample_history[HISTORY_SIZE] = {0};

  // 用于存储输出样本的缓冲区
  q1_31 frame_output[FRAME_SIZE] = {0};

  // 无限循环
  while(1) {
    // 读取一个新的帧。它以相反的顺序放置在sample_history[]的开头
    rx_frame(&sample_history[0], 
             c_audio);

    // 计算FRAME_SIZE个输出样本
    for(int s = 0; s < FRAME_SIZE; s++){
      timer_start(TIMING_SAMPLE);
      frame_output[s] = filter_sample(&sample_history[FRAME_SIZE-s-1]);
      timer_stop(TIMING_SAMPLE);
    }

    // 为新样本腾出空间，放在向量的前面
    memmove(&sample_history[FRAME_SIZE], 
            &sample_history[0], 
            TAP_COUNT * sizeof(int32_t));

    // 发送处理后的帧
    tx_frame(c_audio, 
             &frame_output[0]);
  }
}

在这里，我们可以看到第2A部分中的filter_task()与第1部分中的filter_task()实现非常相似。只是在缓冲区的类型上使用了q1_31，而不是double或float。除此之外，处理过程中涉及的步骤是相同的。

src/part2A/part2A.c
// 接收一帧新的音频数据
static inline 
void rx_frame(
    q1_31 buff[],
    const chanend_t c_audio)
{    
  for(int k = 0; k < FRAME_SIZE; k++)
    buff[FRAME_SIZE-k-1] = (q1_31) chan_in_word(c_audio);

  timer_start(TIMING_FRAME);
}

在第2A部分中，rx_frame()比第1部分中的rx_frame()要简单得多。我们为32位PCM输入分配的指数是-31，这与我们在第1部分将输入转换为浮点数时所做的选择相同。rx_frame()只是从通道c_audio中读取输入样本，并以相反的顺序填充提供的缓冲区。

// 发送一帧新的音频数据
static inline 
void tx_frame(
    const chanend_t c_audio,
    const q1_31 buff[])
{    
  timer_stop(TIMING_FRAME);

  for(int k = 0; k < FRAME_SIZE; k++)
    chan_out_word(c_audio, buff[k]);
}

第2A部分中的tx_frame()也很简单。这些阶段（以及其他所有阶段）关联的输出指数也是-31，因此输出值也采用了q1_31类型，表示其Q1.31格式。

src/part2A/part2A.c
// 应用滤波器生成单个输出样本
q1_31 filter_sample(
    const q1_31 sample_history[TAP_COUNT])
{
  // 滤波器系数关联的指数
  const exponent_t coef_exp = -28;
  // 输入样本关联的指数
  const exponent_t input_exp = -31;
  // 输出样本关联的指数
  const exponent_t output_exp = input_exp;
  // 累加器关联的指数
  const exponent_t acc_exp = input_exp + coef_exp;
  // 将滤波器累加器右移以达到正确的输出指数所需的算术右移位数
  const right_shift_t acc_shr = output_exp - acc_exp;

  // 累加器
  int64_t acc = 0;

  // 对于每个滤波器系数，将64位乘积添加到累加器中
  for(int k = 0; k < TAP_COUNT; k++){
    const int64_t smp = sample_history[k];
    const int64_t coef = filter_coef[k];
    acc += (smp * coef);
  }

  // 应用右移操作，将位深度降至32位
  return sat32(ashr64(acc, acc_shr));
}

这里的filter_sample()接受sample_history[]向量，与之前的阶段一样。通过将32位输入样本与相应的32位滤波器系数相乘，得到64位乘积，然后将64位乘积累加到64位累加器中。

最后，使用了ashr64()和sat32()函数。ashr64()对64位累加器应用算术右移操作，将其右移acc_shr位，并返回64位结果。

来自 misc_func.h 文件：

// 对64位整数进行有符号算术右移
static inline
int64_t ashr64(int64_t x, right_shift_t shr)
{
  int64_t y;
  if(shr >= 0) y = (x >> ( shr) );
  else         y = (x << (-shr) );
  return y;
}

ashr64() 函数对64位整数 x 进行 shr 位的有符号算术右移。它不应用任何饱和逻辑。

sat32() 函数接受一个64位值，并将其限制在32位范围内。这样，无法用 int32_t 表示的值将被饱和到最近可表示的值。

来自 misc_func.h 文件：

// 将64位整数饱和到32位范围内
static inline
int32_t sat32(int64_t x)
{
  if(x <= INT32_MIN) return INT32_MIN;
  if(x >= INT32_MAX) return INT32_MAX;
  return x;
}

第2A部分：定点逻辑​

让我们深入了解第2A部分的 filter_sample() 中使用的逻辑。

在这个阶段，我们的任务是将

yk=∑n=0N−1xk−n⋅bn\begin{aligned} y_k = \sum_{n=0}^{N-1}{ x_{k-n} \cdot b_n } \end{aligned}

转换为定点逻辑。也就是说，yˉ\bar{y}、xˉ\bar{x}和bˉ\bar{b}，它们分别表示一组实数向量，需要用可表示为整数变量和常量的值来替换。

通过将我们的逻辑值展开为可以在代码中使用的对象重新编写方程，我们得到

(y[k]⋅2y^)=∑n=0N−1(x[k−n]⋅2x^)⋅(b[n]⋅2b^)\begin{aligned} (\mathtt{y}[k] \cdot 2^{\hat{y}}) = \sum_{n=0}^{N-1} ({\mathtt{x}[k-n] \cdot 2^{\hat{x}}) \cdot (\mathtt{b}[n]\cdot 2^{\hat{b}}}) \end{aligned}

在这种情况下，我们已经知道

  • N=N = TAP_COUNT =1024 = 1024
  • y^=x^=−31\hat{y} = \hat{x} = -31
  • b^=−28\hat{b} = -28

但我们将推导出更一般情况下的逻辑，其中这些值未知。

信息

我们正在推导出输入和输出指数都是_未知_的情况下的逻辑，但它们仍然是_固定_的。当使用块浮点运算时，我们会遇到输出指数不固定的情况。当输出指数不固定时，输出指数是我们在选择如何实现操作时的额外自由度。

首先，进行一些简化：

y[k]⋅2y^=∑n=0N−1x[k−n]⋅2x^⋅b[n]⋅2b^=∑n=0N−1x[k−n]⋅b[n]⋅2x^+b^=2x^+b^∑n=0N−1x[k−n]⋅b[n]=2x^+b^⋅P\begin{aligned} \mathtt{y}[k] \cdot 2^{\hat{y}} &= \sum_{n=0}^{N-1} {\mathtt{x}[k-n] \cdot 2^{\hat{x}} \cdot \mathtt{b}[n]\cdot 2^{\hat{b}}} \\ &= \sum_{n=0}^{N-1} {\mathtt{x}[k-n] \cdot \mathtt{b}[n]\cdot 2^{\hat{x}+\hat{b}}} \\ &= 2^{\hat{x}+\hat{b}} \sum_{n=0}^{N-1} {\mathtt{x}[k-n] \cdot \mathtt{b}[n]} \\ &= 2^{\hat{x}+\hat{b}} \cdot \mathtt{P} \\ \end{aligned}

其中

P=∑n=0N−1x[k−n]⋅b[n] \mathtt{P} = \sum_{n=0}^{N-1} {\mathtt{x}[k-n] \cdot \mathtt{b}[n]}

注意，P\mathtt{P} 正是在 filter_sample() 的循环中计算的累加器。这告诉我们，(x^+b^)=P^\left(\hat{x}+\hat{b}\right) = \hat{P} 是与累加器相关联的指数。在乘法中，指数相加。

接下来，因为 y^\hat{y} 是固定的，我们只是解出 y[k]\mathtt{y}[k]

y[k]⋅2y^=2x^+b^⋅Py[k]⋅2y^⋅2−y^=2−y^⋅2P^⋅Py[k]=2P^−y^⋅Py[k]=2P^−y^⋅Py[k]=P⋅2−(y^−P^)y[k]=P ≫ (y^−P^)y[k]=P ≫ r⃗\begin{aligned} \mathtt{y}[k] \cdot 2^{\hat{y}} &= 2^{\hat{x}+\hat{b}} \cdot \mathtt{P} \\ \mathtt{y}[k] \cdot 2^{\hat{y}} \cdot 2^{-\hat{y}} &= 2^{-\hat{y}} \cdot 2^{\hat{P}} \cdot \mathtt{P} \\ \mathtt{y}[k] &= 2^{\hat{P}-\hat{y}} \cdot \mathtt{P} \\ \mathtt{y}[k] &= 2^{\hat{P}-\hat{y}} \cdot \mathtt{P} \\ \mathtt{y}[k] &= \mathtt{P} \cdot 2^{-(\hat{y}-\hat{P})} \\ \mathtt{y}[k] &= \mathtt{P} \,\gg\,(\hat{y}-\hat{P}) \\ \mathtt{y}[k] &= \mathtt{P} \,\gg\,\vec{r} \\ \end{aligned}

其中 r⃗=(y^−P^)\vec{r}=(\hat{y}-\hat{P})，我们使用 ≫\mathtt{\gg} 表示对 P\mathtt{P} 进行 r⃗\vec{r} 位的有符号算术右移。

注释：与本教程中使用   ^  \,\,\hat{}\,\, 提示读者变量（例如 y^\hat{y}）是指数一样，  ⃗  \,\,\vec{}\,\, 符号用于提示读者变量（例如 r⃗\vec{r}）表示右移。

"实数" 值的向量将始终使用   ˉ  \,\,\bar{}\,\, 符号表示，而尾数的向量将使用方括号表示，例如 xˉ\bar{x} 和 x[ ]\mathtt{x}[\,]。

现在我们可以找到 r⃗\vec{r}。

r⃗=y^−P^=y^−(x^+b^)=−31−(−31+−28)=28\begin{aligned} \vec{r} &= \hat{y} - \hat{P} \\ &= \hat{y} - (\hat{x}+\hat{b}) \\ &= -31 - (-31 + -28) \\ &= 28 \end{aligned}

因此，在 filter_sample() 中必须对 acc 应用 28 位的右移，这就是 第2A部分 中的 acc_shr。

信息

这不会影响我们的滤波器，但通常情况下，当输出位深度和指数固定时，我们必须意识到溢出或饱和可能是可能的。这与输入指数是否固定无关。原因直接由数学和输出的定义所暗示。

yk=y[k]⋅2y^y[k]=yk⋅2−y^\begin{aligned} y_k &= \mathtt{y}[k]\cdot 2^{\hat{y}} \\ \mathtt{y}[k] &= y_k \cdot 2^{-\hat{y}} \\ \end{aligned}

y[k]\mathtt{y}[k] 的范围由其位深度固定。对于32位值，范围是 [−231,231−1)[-2^{31},2^{31}-1)。那么，避免任何溢出或饱和的 yky_k 范围是

−231≤y[k]<231−231≤yk⋅2−y^<231−231⋅2y^≤yk⋅2−y^⋅2y^<231⋅2y^−231+y^≤yk<231+y^-2^{31} \le \mathtt{y}[k] < 2^{31} \\ -2^{31} \le y_k \cdot 2^{-\hat{y}} < 2^{31} \\ -2^{31} \cdot 2^{\hat{y}} \le y_k \cdot 2^{-\hat{y}} \cdot 2^{\hat{y}} < 2^{31} \cdot 2^{\hat{y}} \\ -2^{31+\hat{y}} \le y_k < 2^{31+\hat{y}} \\

因此，如果底层数学决定 yky_k 在该范围之外（对于某些给定的输入集），那么就无法避免溢出。

对于我们的FIR滤波器来说，这不是一个问题，因为它只是计算一组数字的简单平均值，而数字的平均值永远不会超出这些数字的范围。

结果​

时序​

时序类型测量时间
每个滤波器系数66.99 ns
每个输出样本68593.83 ns
每帧17626584.00 ns

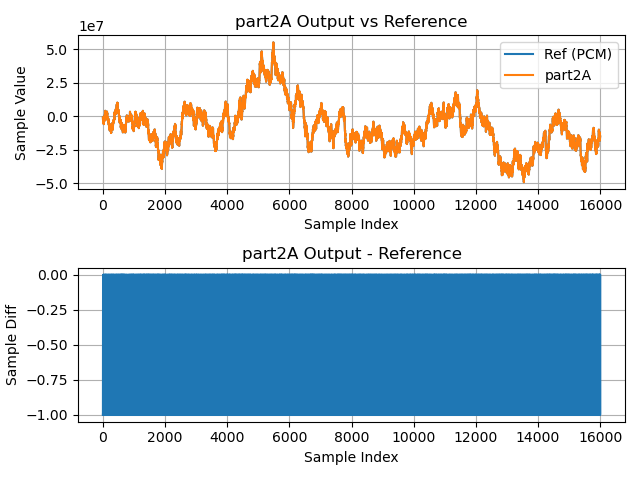
输出波形图​

第2A部分 输出

编辑此页
本文最后由 Vergil Wong 更新于